NCERT Textbook Solutions for Class 12 Mathematics Chapter 2 Inverse Trigonometric Functions in Hindi and English Medium form an essential part of Class 12 Math. NCERT Class 12th Maths Solutions allow us to find the angle when the value of a trigonometric function is known. Chapter 2 in NCERT Exercise Solutions for Class 12 Maths provides a detailed exploration of these functions, making it easier for students to understand the concepts. NCERT Class 12 Maths Textbook Chapter 2 notes cover the definitions, properties and graphs of inverse trigonometric functions, which are useful for solving problems. Whether you’re working through solved examples or practicing important questions, understanding the basic formula sheet is vital.
NCERT Exercise Solutions Class 12 Mathematics Chapter 2 Inverse Trigonometric Functions
Class 12 Maths Chapter 2 MCQ Solutions
NCERT Book Solutions PDF for Chapter 2 also includes step-by-step explanations of questions. This makes it easier to download and revise the concepts anywhere, ensuring you’re fully prepared for exams. NCERT Exercise Solutions for class 12 Maths Chapter 2 Inverse Trigonometric in Hindi and English Medium for revised and updated for 2025-26 exams. Class 12 Maths chapter 2 solutions are modified according to new NCERT books published for academic session 2025-26.
How to Solve NCERT Chapter 2 Questions Effectively
NCERT Detailed Solutions for Class 12 Maths Chapter 2 emphasize a practical approach to solving questions. NCERT Exercises in this chapter test your understanding of inverse trigonometric functions through problems that require simplifying expressions and proving equations. NCERT Class 12th Mathematics Chapter 2 practice questions and revision notes help build confidence in tackling complex problems.
For example, questions often involve finding principal values and determining domains and ranges of functions. Using the NCERT detailed solution guide or PDF download, students can revisit tricky problems. Video lectures also complement the NCERT PDF solutions, as they provide step-by-step walk-through of exercises. Solved examples from NCERT notes are particularly useful for understanding problem-solving techniques. To improve, focus on practice questions and refer to the important formula sheet regularly.
Class 12 Maths Chapter 2 Solutions in Hindi Medium
Preparing for Exams with Class 12 Chapter 2 Resources
Preparation for Class 12 NCERT Mathematics exams requires consistent practice and a clear understanding of key topics. NCERT Class 12th Maths Chapter 2 solutions PDF offers sample papers, previous year questions and MCQs to help students test their knowledge. The chapter’s solved examples provide a thorough review of critical concepts like domains, ranges and properties of inverse trigonometric functions.
NCERT Class 12 Math Textbook Chapter 2 notes and revision materials are ideal for last-minute preparation. Students can also benefit from assignment solutions and problem-solving techniques outlined in the PDF. Solving MCQ and practice questions sharpens problem-solving skills and improves accuracy. With video lectures, detailed explanations and sample papers, students can cover all aspects of Chapter 2 and feel confident about their preparation. This comprehensive approach ensures success in exams.
| Class: 12 | Mathematics |
| Chapter 2: | Inverse Trigonometric Functions |
| Study Material: | Exercise and Extra Questions |
| Content Mode: | Images, Text and Online Videos |
| Academic Session: | 2025-26 |
| Medium: | Hindi and English Medium |
Class 12 Maths Chapter 2 Solutions in English Medium
Important Points in Class 12 Maths Chapter 2 Inverse Trigonometric Functions for Exams
Focus on domains, ranges and principal values of inverse trigonometric functions. Practice solving identities, simplifying expressions and proving equations. Study NCERT solutions for detailed explanations. Revise the formula sheet regularly. Solved examples, MCQs and previous year questions are crucial for mastering problem-solving techniques and preparing effectively for exams.
| Day | Topic | Resources | Tasks |
|---|---|---|---|
| Day 1 | Domains and Ranges | NCERT textbook, formula sheet | Read concepts, practice examples |
| Day 2 | Principal Values | NCERT examples, video lectures | Solve textbook exercises |
| Day 3 | Proving Identities | NCERT solutions PDF | Practice proof-based problems |
| Day 4 | Simplifying Expressions | Practice questions, solved examples | Solve additional practice questions |
| Day 5 | Revision | MCQs, previous year questions | Review mistakes, revisit weak topics |
NCERT Solutions for class 12 Maths Chapter 2
Download the NCERT solutions of class xii Maths chapter 2 Hindi as well as English Medium free to use online or in PDF format including miscellaneous exercise and practice books based on NCERT Books with solutions and answers. Download offline apps based on latest CBSE Syllabus. The given NCERT Solutions Apps updated for new academic session 2025-26. The Previous Years Papers are to know the type and pattern of the questions asked which are designed as per latest CBSE Syllabus
Class 12 Maths Chapter 2 Study Material
Inverse Trigonometric Functions
We know that a function has inverse if and only if it is one – one and onto. There are many functions like trigonometric functions are not one – one or onto because these functions periodic so these are many one. In order to get inverse of these functions, we must restrict their domain and co-domain in such a way that they become one – one and onto and these restricted values are known as principle values.

There are some important theorems/ properties of inverse trigonometric functions. It is important to know that how to convert one function into the terms of others.
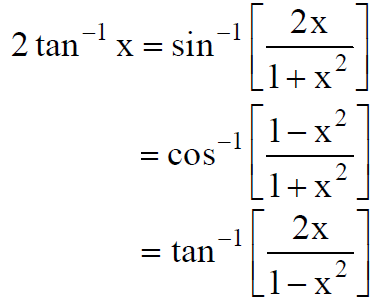
Complement functions are useful during the conversion of one functions into it complimentary functions.
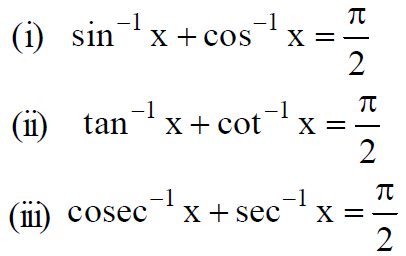
During the application of addition formula of tan, we should know that whether the product of x and y is greater than 1 or not. If it is more than 1, use the above formula and then apply the following formula.
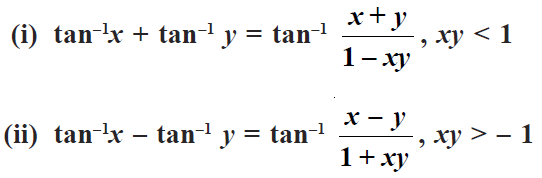
Important Questions on 12th Maths Chapter 2
Solve for x: 2 tan⁻¹(cos x) = tan⁻¹( 2cosec x)
Given that 2tan⁻¹(cosx) = tan⁻¹(2cosecx)
⇒ tan⁻¹(2cosx/(1-cos²x)) = tan⁻¹(2cosecx) [as 2 tan⁻¹x = tan⁻¹(2x/(1-x²)]
⇒ 2 cosx/(1 – cos²x) = 2cosecx
⇒ 2 cosx/(sin²x) = 2/sinx
⇒ 2 sin x.cos x = 2 sin² x
⇒ 2 sin x.cos x – 2 sin² x = 0
⇒ 2 sin x (cos x – sin x) = 0
⇒ 2 sin x = 0 or cos x – sin x = 0
But sin x ≠ 0 as it does not satisfy the equation.
∴ cos x – sin x = 0
⇒ cos x = sin x
⇒ tan x = 1
∴ x = π/4
Find the principal value of sin⁻¹(-1/2)
Let sin⁻¹(-1/2) = y, then sin y = -1/2 = – sin(π/6) = sin(-π/6)
We know that the range of the principal value branch of sin⁻¹ is [-π/2, π/2] and sin(-π/6) = -1/2
Therefore, the principal value of sin⁻¹(-1/2) is -π/6.
Find the principal value of tan⁻¹(−1).
Let tan⁻¹(−1) = y.
Then, tan y = -1 = – tan(π/4) = tan(-π/4)
We know that the range of the principal value branch of tan⁻¹ is (-π/2,π/2) and tan(-π/4) = -1
Therefore, the principal value of tan⁻¹(−1) is -π/4.
Trigonometry – Historical Facts!
The study of trigonometric functions started in 2nd millennium BC but in India it flourished in the Gupta Period due to Aryabhata. During the middle age, the study of trigonometry continued in Islamic Maths. The modern form of trigonometry functions were being used since 17th century by famous mathematician Isaac Newton, James Stirling etc.
What are inverse trigonometric functions and why are they important in Class 12 Maths?
Inverse trigonometric functions help determine the angles when the values of trigonometric functions like sine, cosine or tangent are known. These functions play a vital role in higher-level mathematics, particularly in calculus. Chapter 2 of NCERT Class 12 Mathematics textbook provides a thorough explanation of these functions, including their domains, ranges, and principal values. By studying the NCERT Exercise solutions for Class 12 Maths Chapter 2, students can learn the step-by-step techniques for solving problems involving inverse trigonometric functions. Practicing from the NCERT Class 12 Maths Chapter 2 PDF download will ensure clarity and exam readiness.
What are the basic uses of inverse trigonometric functions chapter 2 of class 12th Mathematics?
The inverse trigonometric functions play an important role in calculus. The concepts of inverse trigonometric functions are also used in science and engineering. Inverse trigonometric functions are widely used in the navigation, physics, geometry, construction, and architecture. Also, an example of the use of inverse trigonometric functions in the real world is Carpentry.
How can I effectively solve problems from NCERT Class 12 Maths Chapter 2?
To effectively solve problems on inverse trigonometric functions, start with understanding the basic concepts and formulas provided in NCERT Class 12 Mathematics Book Chapter 2 notes. Focus on solved examples and practice questions that cover different types of problems, such as proving identities and simplifying expressions. NCERT PDF solutions for Class 12 Math Book Chapter 2 PDF offers step-by-step answers that are easy to follow. Regularly revisiting the formula sheet and solving previous year questions will help you master this chapter. Video lectures and assignment solutions also provide additional support for tackling challenging questions.
What are the main points of chapter 2 of grade 12th Maths to remember at the time of board exams?
If students remember below mentioned points of chapter 2 of class 12th Maths on tips, they can quickly solve questions of chapter 2 in the board exams:
- Functions Domain Range (Principal Value Branches)
y=sin⁻¹x [-1,1] [-π/2, π/2]
y= cos⁻¹x [-1,1] [0, π]
y=cosec⁻¹x R-(-1,1) [-π/2, π/2]-{0}
y=sec⁻¹x R-(-1,1) [0, π]-{ π/2}
y=tan⁻¹x R (-π/2, π/2)
y=cot⁻¹x R (0, π) - sin⁻¹x should not be confused with (sin x)⁻¹. In fact (sin x)⁻¹=1/sin x and similarly for other trigonometric functions.
- Whenever no branch of an inverse trigonometric functions is mentioned, we mean the principal value branch of that function.
- The value of an inverse trigonometric functions which lies in the range of principal branch is called the principal value of that inverse trigonometric functions.
- All the properties of inverse trigonometric functions mentioned in section 2.3 of chapter 2 of class 12th Maths.
What resources are available for NCERT Class 12 Maths Chapter 2 preparation?
For comprehensive preparation, students can use the NCERT Class 12 Maths Chapter 2 solutions PDF, which includes solved examples, exercises and revision notes. NCERT Class 12 Mathematics Chapter 2 practice questions are ideal for understanding key topics like domains, ranges and properties of inverse trigonometric functions. Video lectures, important formula sheets and sample papers help reinforce the concepts. Students can download the NCERT Class 12 Maths Chapter 2 PDF and access MCQs, previous year questions and problem-solving techniques to improve their understanding and confidence in this chapter.
How many sums are there in chapter 2 of class 12th Maths in First Term Exam?
There are three exercises in chapter 2 of class 12th Maths.
In the first exercise (Ex 2.1), there are two examples (examples 1, 2) and 14 questions.
The second exercise (Ex 2.2) has 6 examples (Examples 3, 4, 5, 6, 7, 8) and 21 questions.
The last (Miscellaneous) exercise contains five examples (examples 9, 10, 11, 12, 13) and 17 questions.
So, there are in all 65 problems (13 examples and 52 questions) in chapter 2 of class 12th Maths.
How can I prepare for Class 12 Maths exams using Chapter 2 resources?
To prepare for exams, start with the NCERT solutions for Class 12 Maths Chapter 2, which cover all exercise problems in detail. Focus on revising important concepts like principal values and the graphs of inverse trigonometric functions. Use NCERT Class 12 Mathematics Chapter 2 notes and revision materials to reinforce key topics. Solving sample papers, MCQ and previous year questions will help you identify weak areas. NCERT Class 12 Maths Exercise Chapter 2 PDF also includes a detailed solution guide and problem-solving techniques that are perfect for exam preparation.
What are the basic terms to understand chapter 2 of class 12th Maths easily?
To understand chapter 2 of class 12th Maths easily, students should revise below mentioned topics before starting chapter 2 of 12th Maths:
1. Chapter 3 (Trigonometric Functions) of class 11th Maths.
2. Invertible functions (chapter 1 of class 12th Maths).
Are solved examples in NCERT Class 12 Maths Chapter 2 helpful?
Yes, solved examples in NCERT Class 12 Maths Chapter 2 are highly helpful for understanding the application of inverse trigonometric functions. They provide step-by-step solutions, which are easy to follow and replicate in practice questions. By referring to the NCERT Class 12 Maths Textbook Chapter 2 solutions PDF, students can study these examples in detail and strengthen their problem-solving techniques. Solved examples often illustrate concepts like simplifying expressions, proving identities and finding domains and ranges. These examples, combined with practice questions, revision notes and Objective Questions, ensure a thorough understanding of the chapter.


