A 1.2 m tall girl spots a balloon moving with the wind in a horizontal

Updated on December 6, 2023
by Tiwari Academy

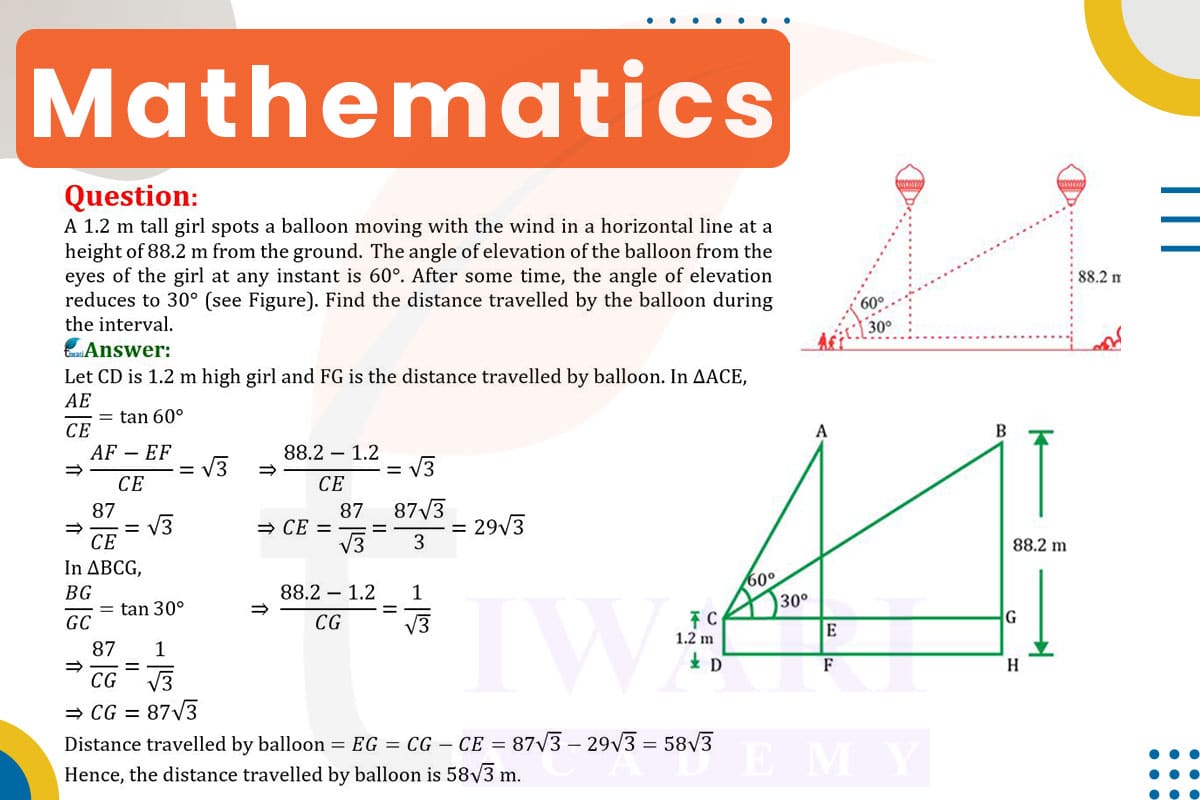
To find the distance traveled by the balloon, we use trigonometry. Let’s denote the initial and final distances from the girl to the balloon as d1 and d2, respectively.
Initial Position (60° Angle of Elevation): The height of the balloon from the girl’s eyes is 88.2 m − 1.2 m = 87 m. Using tan(60°) = √3, the equation is √3 = 87/d1. Solving for d1, we get d1 = 87/√3.
Final Position (30° Angle of Elevation): Using tan(30°) = 1/√3, the equation is 1/√3 = 87/d2. Solving for d2, we get d2 = 87√3. The distance traveled by the balloon is d2 − d1 = 87√3 − 87/√3, which simplifies to approximately 101.82 meters. Therefore, the balloon traveled about 101.82 meters during the interval.

A 1.2 m tall girl spots a balloon moving with the wind in a horizontal line at a height of 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is 60°. After some time, the angle of elevation reduces to 30°. Find the distance travelled by the balloon during interval.

Let’s discuss in detail

Trigonometric Application in Motion Analysis

Trigonometry, a branch of mathematics, is extensively used in analyzing motion, especially in scenarios involving angles and distances. The problem at hand involves a balloon moving horizontally at a certain height and a girl observing it from the ground. By using the angles of elevation at different instances, we aim to calculate the distance traveled by the balloon. This scenario is a practical demonstration of how trigonometry can be applied to solve real-world problems in physics and engineering, particularly in motion analysis and tracking moving objects.

Understanding the Problem: Balloon Observation

The problem presents a 1.2-meter-tall girl observing a balloon that is initially 88.2 meters above the ground. The angle of elevation from the girl’s eyes to the balloon changes from 60° to 30° over a period. The objective is to determine the distance the balloon has traveled during this interval. This setup forms two right-angled triangles at different instances – one at the initial position (60° angle) and the other at the final position (30° angle).

The Role of Tangent in Angle of Elevation

In trigonometry, the tangent of an angle in a right-angled triangle is the ratio of the length of the opposite side (height difference between the girl’s eyes and the balloon) to the length of the adjacent side (horizontal distance from the girl to the balloon). By applying the tangent function to the given angles of elevation, we can calculate the distances of the balloon from the girl at both the initial and final positions.

Calculating the Initial Distance
For the initial position with a 60° angle of elevation, we use the formula tan(60°) = √3. The height difference is 88.2 m − 1.2 m = 87 m. So, √3 = 87/d1, where d1 is the initial distance. Solving for d1, we find d1 = 87/√3 meters.

Determining the Final Distance

At the final position with a 30° angle of elevation, we apply the formula tan(30°) = 1/√3. The equation becomes 1/√3 = 87/d2, where d2 is the final distance. Solving for d2, we find
d2 = 87√3 meters.

Calculating the Distance Traveled by the Balloon

The distance traveled by the balloon is the difference between d2 and d1, which is 87√3 − 87/√3 meters. This calculation simplifies to approximately 101.82 meters. This example illustrates the practical application of trigonometry in motion analysis, demonstrating its importance in tracking and measuring the movement of objects. Trigonometry provides a reliable mathematical approach to solving problems where direct measurement of distance is challenging, ensuring accuracy and efficiency in analysis and planning.

Discuss this question in detail or visit to Class 10 Maths Chapter 9 for all questions.
Questions of 10th Maths Exercise 9.1 in Detail

A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole, if the angle made by the rope with the ground level is 30°.

A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree.

A contractor plans to install two slides for the children to play in a park. For the children below the age of 5 years, she prefers to have a slide whose top is at a height of 1.5 m, and is inclined at an angle of 30° to the ground, whereas for elder children, she wants to have a steep slide at a height of 3m, and inclined at an angle of 60° to the ground. What should be the length of the slide in each case?

The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower is 30°. Find the height of the tower.

A kite is flying at a height of 60 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in the string.

A 1.5 m tall boy is standing at some distance from a 30 m tall building. The angle of elevation from his eyes to the top of the building increases from 30° to 60° as he walks towards the building. Find the distance he walked towards the building.

From a point on the ground, the angles of elevation of the bottom and the top of a transmission tower fixed at the top of a 20 m high building are 45° and 60° respectively. Find the height of the tower.

A statue, 1.6 m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60° and from the same point the angle of elevation of the top of the pedestal is 45°. Find the height of the pedestal.

The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 50 m high, find the height of the building.

Two poles of equal heights are standing opposite each other on either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60° and 30°, respectively. Find the height of the poles and the distances of the point from the poles.

A TV tower stands vertically on a bank of a canal. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From another point 20 m away from this point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30°. Find the height of the tower and the width of the canal.