The angle of elevation of the top of a building from the foot

Updated on December 6, 2023
by Tiwari Academy

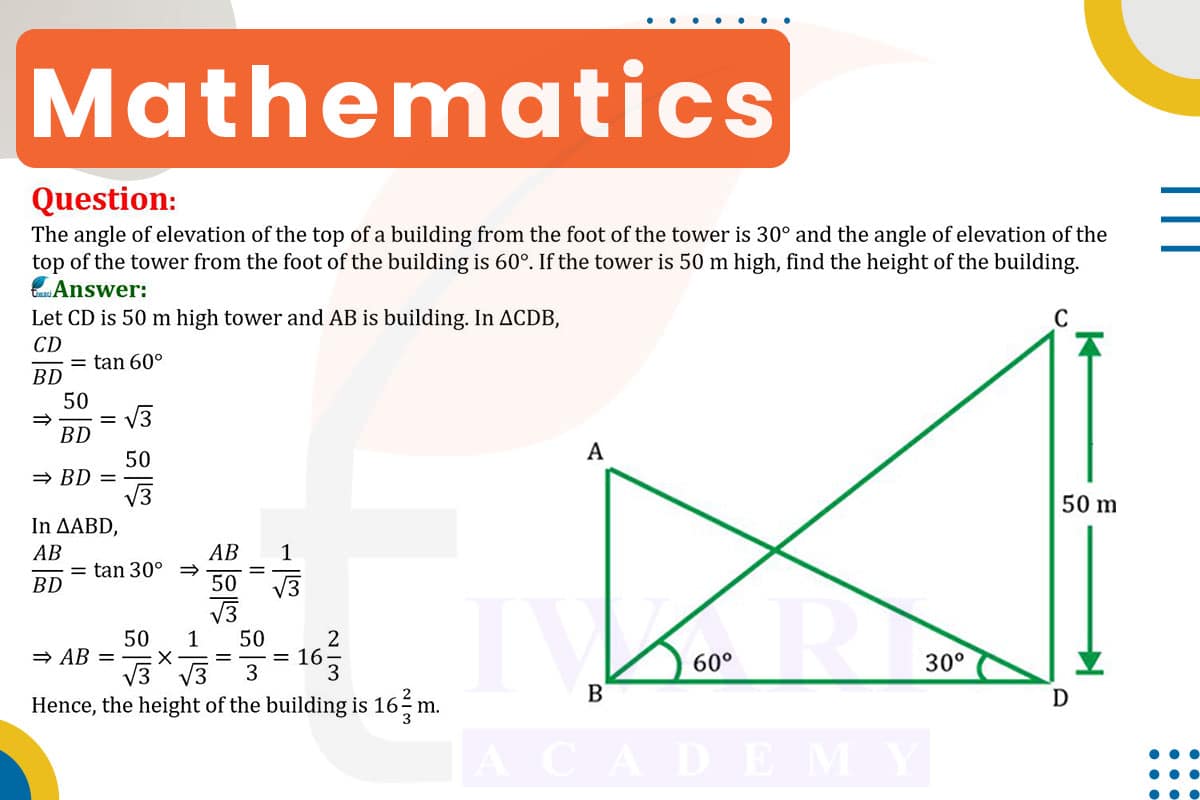
To find the height of the building, we use trigonometry, specifically the tangent function. Let’s denote the height of the building as h and the distance between the building and the tower as d.
Angle of Elevation to Top of Tower (60°): Using tan(60°) = √3, the equation is √3 = 50/d. Solving for d, we get d = 50/√3.
Angle of Elevation to Top of Building (30°): Using tan(30°) = 1/√3, the equation is 1/√3 = h/d. Substituting d, we get 1/√3 = h/(50/√3).
Solving for h, we find h = 50/3, which is approximately 16.67 meters. Therefore, the height of the building is about 16.67 meters.

The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 50 m high, find the height of building.

Let’s discuss in detail

Trigonometric Solutions in Architecture

Trigonometry, a branch of mathematics, plays a crucial role in architecture and construction, particularly in determining the heights of structures when direct measurement is not possible. The problem at hand involves finding the height of a building using the angles of elevation from the foot of a nearby tower and vice versa. This scenario is a classic example of how trigonometry can be applied to solve practical problems in architectural design and urban planning, demonstrating the utility of mathematical concepts in real-world applications.

Intersecting Lines of Sight

The problem presents two structures: a tower and a building. The angle of elevation to the top of the tower from the foot of the building is 60°, and the angle of elevation to the top of the building from the foot of the tower is 30°. The height of the tower is given as 50 meters. The objective is to determine the height of the building. This setup forms two right-angled triangles, one with the tower and one with the building, sharing a common horizontal distance.

The Role of Tangent in Angle of Elevation

In trigonometry, the tangent of an angle in a right-angled triangle is the ratio of the length of the opposite side (height of the structure) to the length of the adjacent side (horizontal distance between the structures). By applying the tangent function to the given angles of elevation, we can calculate the heights and distances involved in the problem.

Calculating the Distance Between the Tower and the Building
First, we calculate the distance between the tower and the building using the 60° angle of elevation to the top of the tower. The tangent of 60° is √3, so the equation is tan(60°) = (50 m)/d, where d is the distance. Solving for d, we find d = 50/√3 meters.

Determining the Height of the Building

Next, we use the 30° angle of elevation to find the height of the building. Applying tan(30°) = 1/√3, the equation is 1/√3 = h/d, where h is the height of the building. Substituting the previously calculated value of d, we get 1/√3 = h/(50/√3). Solving for h, we find h = 50/3 meters.

Trigonometry in Determining Building Heights

The height of the building, calculated to be approximately 16.67 meters, demonstrates the practical application of trigonometry in architectural and construction scenarios. This method is particularly useful in urban environments where direct measurement of heights can be challenging. Trigonometry not only provides a mathematical solution to these problems but also ensures accuracy and efficiency in planning and design. This scenario underscores the importance of trigonometry in real-life applications, bridging the gap between theoretical mathematics and practical problem-solving in the field of architecture.

Discuss this question in detail or visit to Class 10 Maths Chapter 9 for all questions.
Questions of 10th Maths Exercise 9.1 in Detail

A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole, if the angle made by the rope with the ground level is 30°.

A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree.

A contractor plans to install two slides for the children to play in a park. For the children below the age of 5 years, she prefers to have a slide whose top is at a height of 1.5 m, and is inclined at an angle of 30° to the ground, whereas for elder children, she wants to have a steep slide at a height of 3m, and inclined at an angle of 60° to the ground. What should be the length of the slide in each case?

The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower is 30°. Find the height of the tower.

A kite is flying at a height of 60 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in the string.

A 1.5 m tall boy is standing at some distance from a 30 m tall building. The angle of elevation from his eyes to the top of the building increases from 30° to 60° as he walks towards the building. Find the distance he walked towards the building.

From a point on the ground, the angles of elevation of the bottom and the top of a transmission tower fixed at the top of a 20 m high building are 45° and 60° respectively. Find the height of the tower.

A statue, 1.6 m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60° and from the same point the angle of elevation of the top of the pedestal is 45°. Find the height of the pedestal.

The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 50 m high, find the height of the building.

Two poles of equal heights are standing opposite each other on either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60° and 30°, respectively. Find the height of the poles and the distances of the point from the poles.

A TV tower stands vertically on a bank of a canal. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From another point 20 m away from this point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30°. Find the height of the tower and the width of the canal.