As observed from the top of a 75 m high lighthouse from the sea-level

Updated on December 6, 2023
by Tiwari Academy

To find the distance between the two ships, we use trigonometry, specifically the tangent function related to the angles of depression. The angles of depression from the lighthouse to the ships are the same as the angles of elevation from the ships to the top of the lighthouse.
For the Ship at 30° Angle of Depression: Using tan(30°) = 1/√3, the distance to the first ship (d1) is given by 1/√3 = 75/d1. Solving for d1, we get d1 = 75√3.
For the Ship at 45° Angle of Depression: Using tan(45°) = 1, the distance to the second ship (d2) is d2 = 75 m.
The distance between the two ships is d1 − d2 = 75√3 − 75, which simplifies to approximately 44.98 meters. Therefore, the distance between the two ships is about 44.98 meters.

As observed from the top of a 75 m high lighthouse from the sea-level, the angles of depression of two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between two ships.

Let’s discuss in detail

Trigonometric Analysis in Nautical Navigation

Trigonometry, a fundamental branch of mathematics, is extensively used in nautical navigation, particularly for determining distances and angles from a fixed point. The problem at hand involves the use of trigonometry to calculate the distance between two ships as observed from the top of a lighthouse. By analyzing the angles of depression to the ships, we can determine their distances from the lighthouse and subsequently the distance between them. This scenario is a practical demonstration of how trigonometry can be applied in maritime navigation and safety.

Understanding the Problem: Lighthouse Observation

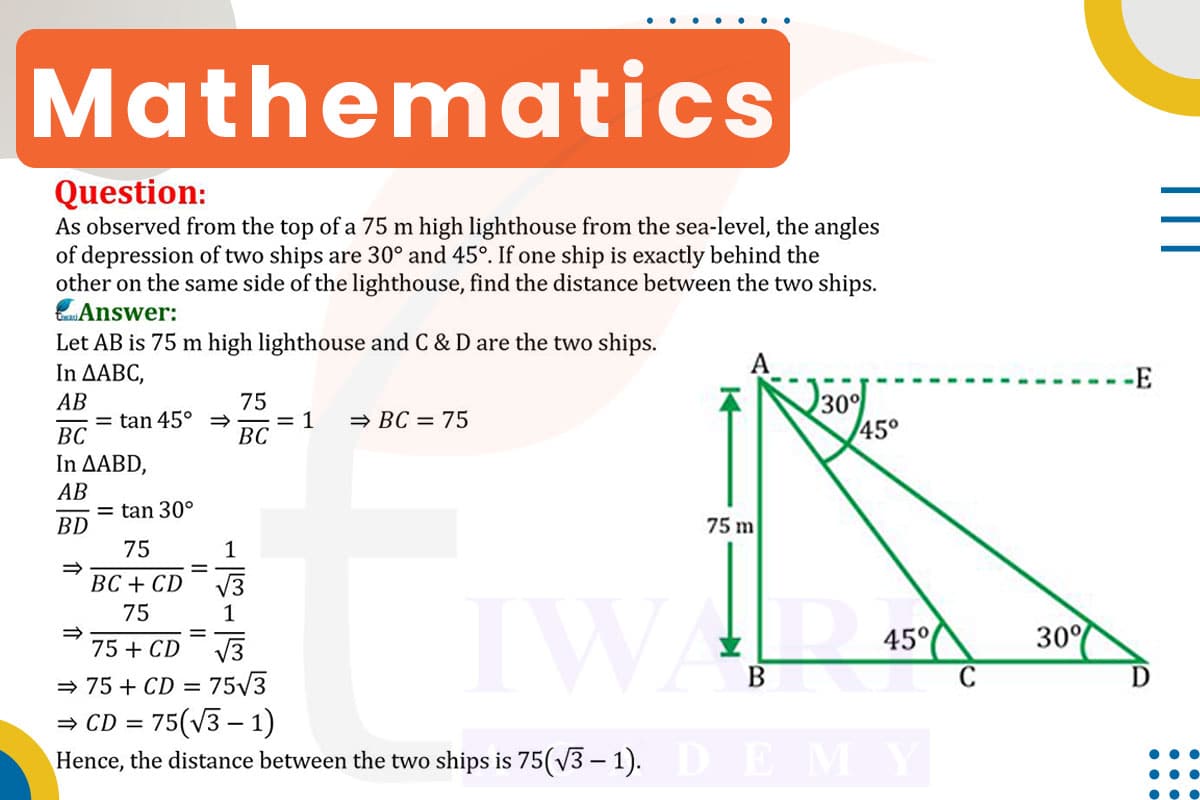
The problem presents a lighthouse that is 75 meters high. From the top of this lighthouse, the angles of depression to two ships are observed to be 30° and 45°, respectively. The ships are located on the same side of the lighthouse, with one directly behind the other. The objective is to find the distance between these two ships. This setup forms two right-angled triangles, one with each ship, with the lighthouse as the common vertex.

The Role of Tangent in Angle of Depression

In trigonometry, the tangent of an angle in a right-angled triangle is the ratio of the length of the opposite side to the length of the adjacent side. The angles of depression from the lighthouse are equivalent to the angles of elevation from the ships to the lighthouse. By applying the tangent function to these angles, we can calculate the distances of the ships from the lighthouse.

Calculating the Distance to the First Ship
For the ship at a 30° angle of depression, we use the tangent function. The equation is tan(30°) = 1/√3 = 75/d1, where d1 is the distance to the first ship. Solving for d1, we find d1 = 75√3 meters. This distance is crucial for determining the relative positioning of the two ships.

Determining the Distance to the Second Ship

Next, we apply the tangent function to the 45° angle of depression for the second ship. The equation is tan(45°) = 1 = 75/d2, where d2 is the distance to the second ship. Since
tan(45°) = 1, it follows that d2 is equal to 75 meters.

Calculating the Distance Between the Ships

The distance between the two ships is the difference between d1 and d2, which is 75√3 − 75 meters. This calculation simplifies to approximately 44.98 meters. This example illustrates the practical application of trigonometry in maritime navigation, demonstrating how it can provide accurate measurements for safety and operational purposes. Trigonometry proves to be an invaluable tool in nautical scenarios, offering a mathematical approach to solving problems where direct measurement is challenging or impossible.

Discuss this question in detail or visit to Class 10 Maths Chapter 9 for all questions.
Questions of 10th Maths Exercise 9.1 in Detail

A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole, if the angle made by the rope with the ground level is 30°.

A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree.

A contractor plans to install two slides for the children to play in a park. For the children below the age of 5 years, she prefers to have a slide whose top is at a height of 1.5 m, and is inclined at an angle of 30° to the ground, whereas for elder children, she wants to have a steep slide at a height of 3m, and inclined at an angle of 60° to the ground. What should be the length of the slide in each case?

The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower is 30°. Find the height of the tower.

A kite is flying at a height of 60 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in the string.

A 1.5 m tall boy is standing at some distance from a 30 m tall building. The angle of elevation from his eyes to the top of the building increases from 30° to 60° as he walks towards the building. Find the distance he walked towards the building.

From a point on the ground, the angles of elevation of the bottom and the top of a transmission tower fixed at the top of a 20 m high building are 45° and 60° respectively. Find the height of the tower.

A statue, 1.6 m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60° and from the same point the angle of elevation of the top of the pedestal is 45°. Find the height of the pedestal.

The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 50 m high, find the height of the building.

Two poles of equal heights are standing opposite each other on either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60° and 30°, respectively. Find the height of the poles and the distances of the point from the poles.

A TV tower stands vertically on a bank of a canal. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From another point 20 m away from this point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30°. Find the height of the tower and the width of the canal.