The angle of elevation of the top of a tower from a point on ground

Updated on December 4, 2023
by Tiwari Academy

To find the height of the tower, we use trigonometry, specifically the tangent function. The tangent of an angle in a right-angled triangle is the ratio of the opposite side (height of the tower) to the adjacent side (distance from the tower).
Given: Distance from the tower = 30 m, Angle of elevation = 30°. The tangent of 30° is 1/√3.
Using the formula tan(30°) = (height of the tower)/(30 m), we have 1/√3 = (height of the tower)/30.
Solving for the height of the tower, we get height of the tower = 30/√3, which simplifies to approximately 17.32 meters. Therefore, the height of the tower is about 17.32 meters.

The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower, is 30°. Find the height of tower.

Let’s discuss in detail

Introduction to Trigonometric Height Measurement

Trigonometry, a branch of mathematics, is extensively used in various fields, including engineering, astronomy, and geography, for measuring heights and distances. One common application is determining the height of inaccessible objects, such as towers, using the principles of trigonometry. The problem at hand involves calculating the height of a tower using the angle of elevation from a certain distance. This scenario is a classic example of a real-world application of trigonometry, demonstrating how mathematical concepts can be practically applied to solve everyday problems.

Measuring a Tower’s Height

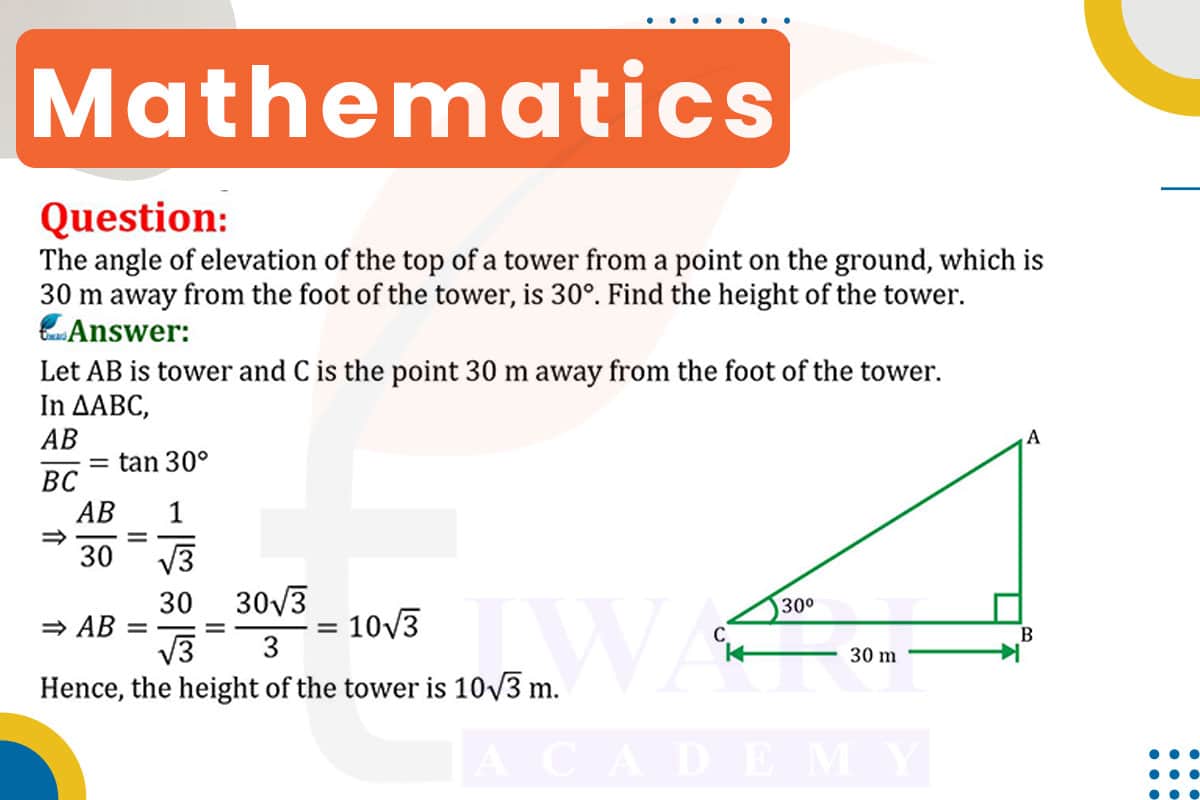
The problem involves a tower and a point on the ground 30 meters away from the base of the tower. The angle of elevation from this point to the top of the tower is 30°. The goal is to find the height of the tower. This scenario forms a right-angled triangle with the tower as the opposite side, the distance from the tower as the adjacent side, and the angle of elevation at the point on the ground.

The Role of Tangent in Trigonometry

In trigonometry, the tangent of an angle in a right-angled triangle is the ratio of the length of the opposite side to the length of the adjacent side. In this case, the tangent function is ideal for finding the height of the tower, as we have the angle of elevation (30°) and the distance from the tower (30 meters), and we need to find the height of the tower (opposite side).

Applying the Tangent Function
Applying the tangent function to the 30° angle, we use the formula tan(30°) = (height of the tower)/(distance from the tower). The tangent of 30° is a known value, 1/√3. Substituting the known values into the formula, we get 1/√3 = (height of the tower)/(30 m).

Calculating the Height of the Tower

Solving the equation for the height of the tower, we multiply both sides by 30 meters. This gives us height of the tower = 30 m × 1/√3. Simplifying this equation, we find that the height of the tower is approximately 17.32 meters. This calculation demonstrates how trigonometry can be effectively used to solve problems involving angles and distances in real-world scenarios.

Practical Applications of Trigonometry

This example highlights the practicality of trigonometry in real-life situations. The ability to calculate unknown heights using angles and distances is invaluable in many fields, from construction to navigation. Trigonometry bridges the gap between theoretical mathematics and practical applications, showcasing the importance of mathematical concepts in solving real-world problems. This scenario, in particular, illustrates how trigonometry can provide solutions in situations where direct measurement is not feasible.

Discuss this question in detail or visit to Class 10 Maths Chapter 9 for all questions.
Questions of 10th Maths Exercise 9.1 in Detail

A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole, if the angle made by the rope with the ground level is 30°.

A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree.

A contractor plans to install two slides for the children to play in a park. For the children below the age of 5 years, she prefers to have a slide whose top is at a height of 1.5 m, and is inclined at an angle of 30° to the ground, whereas for elder children, she wants to have a steep slide at a height of 3m, and inclined at an angle of 60° to the ground. What should be the length of the slide in each case?

The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower is 30°. Find the height of the tower.

A kite is flying at a height of 60 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in the string.

A 1.5 m tall boy is standing at some distance from a 30 m tall building. The angle of elevation from his eyes to the top of the building increases from 30° to 60° as he walks towards the building. Find the distance he walked towards the building.

From a point on the ground, the angles of elevation of the bottom and the top of a transmission tower fixed at the top of a 20 m high building are 45° and 60° respectively. Find the height of the tower.

A statue, 1.6 m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60° and from the same point the angle of elevation of the top of the pedestal is 45°. Find the height of the pedestal.

The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 50 m high, find the height of the building.

Two poles of equal heights are standing opposite each other on either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60° and 30°, respectively. Find the height of the poles and the distances of the point from the poles.

A TV tower stands vertically on a bank of a canal. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From another point 20 m away from this point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30°. Find the height of the tower and the width of the canal.