From a point on the ground, the angles of elevation of the bottom

Updated on December 4, 2023
by Tiwari Academy

To find the height of the transmission tower, we use trigonometry, specifically the tangent function. Let’s denote the total height of the building and tower as H and the height of the building as 20 m.
Angle of Elevation to Top of Tower (60°): Using tan(60°) = √3, the equation is √3 = H/d, where d is the distance from the point to the building.
Angle of Elevation to Bottom of Tower (45°): Using tan(45°)=1, the equation is 1 = 20/d. So, d = 20 m.
Substituting d in the first equation, √3 = H/20. Solving for H, we get H = 20√3 m. The height of the tower is H − 20 m, which is 20√3 − 20 m, approximately 14.64 meters. Therefore, the height of the tower is about 14.64 meters.

From a point on the ground, the angles of elevation of the bottom and the top of a transmission tower fixed at the top of a 20 m high building are 45° and 60° respectively. Find the height of tower.

Let’s discuss in detail

Trigonometric Analysis in Structural Height Measurement

Trigonometry, a crucial branch of mathematics, is extensively used in various practical applications, including architecture and engineering. One such application is determining the height of structures, such as transmission towers, when direct measurement is not feasible. The problem at hand involves using the angles of elevation to the bottom and the top of a transmission tower mounted on a building to find the tower’s height. This scenario exemplifies how trigonometry can be applied to solve real-world problems, particularly in situations where direct measurements are challenging or impossible.

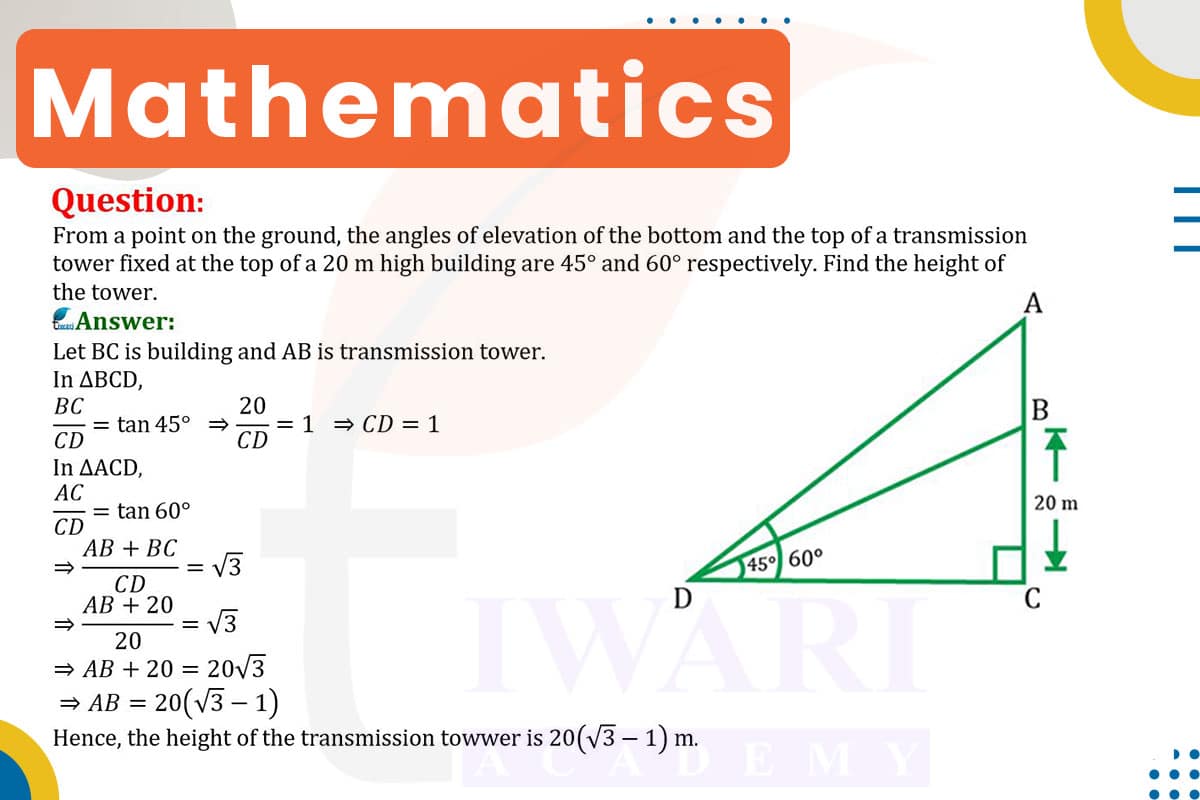
Understanding the Problem: Angles of Elevation to a Tower

The problem presents a transmission tower fixed atop a 20-meter-high building. From a certain point on the ground, the angles of elevation to the bottom and the top of the tower are 45° and 60°, respectively. The goal is to determine the height of the transmission tower. This setup forms two right-angled triangles – one from the point to the top of the tower and another from the point to the bottom of the tower (top of the building).

The Role of Tangent in Angle of Elevation

In trigonometry, the tangent of an angle in a right-angled triangle is the ratio of the length of the opposite side to the length of the adjacent side. This function is particularly useful in scenarios where the height of an object (opposite side) needs to be determined from a specific distance (adjacent side). By applying the tangent function to the given angles of elevation, we can calculate the distances involved and, subsequently, the height of the tower.

Calculating the Distance to the Building
First, we calculate the distance from the point to the building using the 45° angle of elevation to the building’s top. The tangent of 45° is 1, so the equation is tan(45°) = 20 /d, where d is the distance. Since tan(45°) = 1, it follows that d = 20 meters. This distance is crucial for calculating the total height from the point to the top of the tower.

Determining the Total Height to the Tower’s Top

Next, we use the 60° angle of elevation to find the total height from the point to the top of the tower. Applying tan(60°) = √3, the equation is √3 = H/20, where H is the total height. Solving for H, we get H = 20√3 meters. This height includes both the building and the tower.

Calculating the Transmission Tower’s Height

The height of the transmission tower is the total height minus the building’s height. Therefore, the tower’s height is 20√3 − 20 meters, which simplifies to approximately 14.64 meters. This calculation not only demonstrates the practical application of trigonometry in determining structural heights but also highlights the importance of mathematical principles in engineering and architectural design. Trigonometry proves to be an invaluable tool in scenarios where direct measurement is impractical, offering a reliable method for accurate estimation and design.

Discuss this question in detail or visit to Class 10 Maths Chapter 9 for all questions.
Questions of 10th Maths Exercise 9.1 in Detail

A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole, if the angle made by the rope with the ground level is 30°.

A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree.

A contractor plans to install two slides for the children to play in a park. For the children below the age of 5 years, she prefers to have a slide whose top is at a height of 1.5 m, and is inclined at an angle of 30° to the ground, whereas for elder children, she wants to have a steep slide at a height of 3m, and inclined at an angle of 60° to the ground. What should be the length of the slide in each case?

The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower is 30°. Find the height of the tower.

A kite is flying at a height of 60 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in the string.

A 1.5 m tall boy is standing at some distance from a 30 m tall building. The angle of elevation from his eyes to the top of the building increases from 30° to 60° as he walks towards the building. Find the distance he walked towards the building.

From a point on the ground, the angles of elevation of the bottom and the top of a transmission tower fixed at the top of a 20 m high building are 45° and 60° respectively. Find the height of the tower.

A statue, 1.6 m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60° and from the same point the angle of elevation of the top of the pedestal is 45°. Find the height of the pedestal.

The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 50 m high, find the height of the building.

Two poles of equal heights are standing opposite each other on either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60° and 30°, respectively. Find the height of the poles and the distances of the point from the poles.

A TV tower stands vertically on a bank of a canal. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From another point 20 m away from this point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30°. Find the height of the tower and the width of the canal.