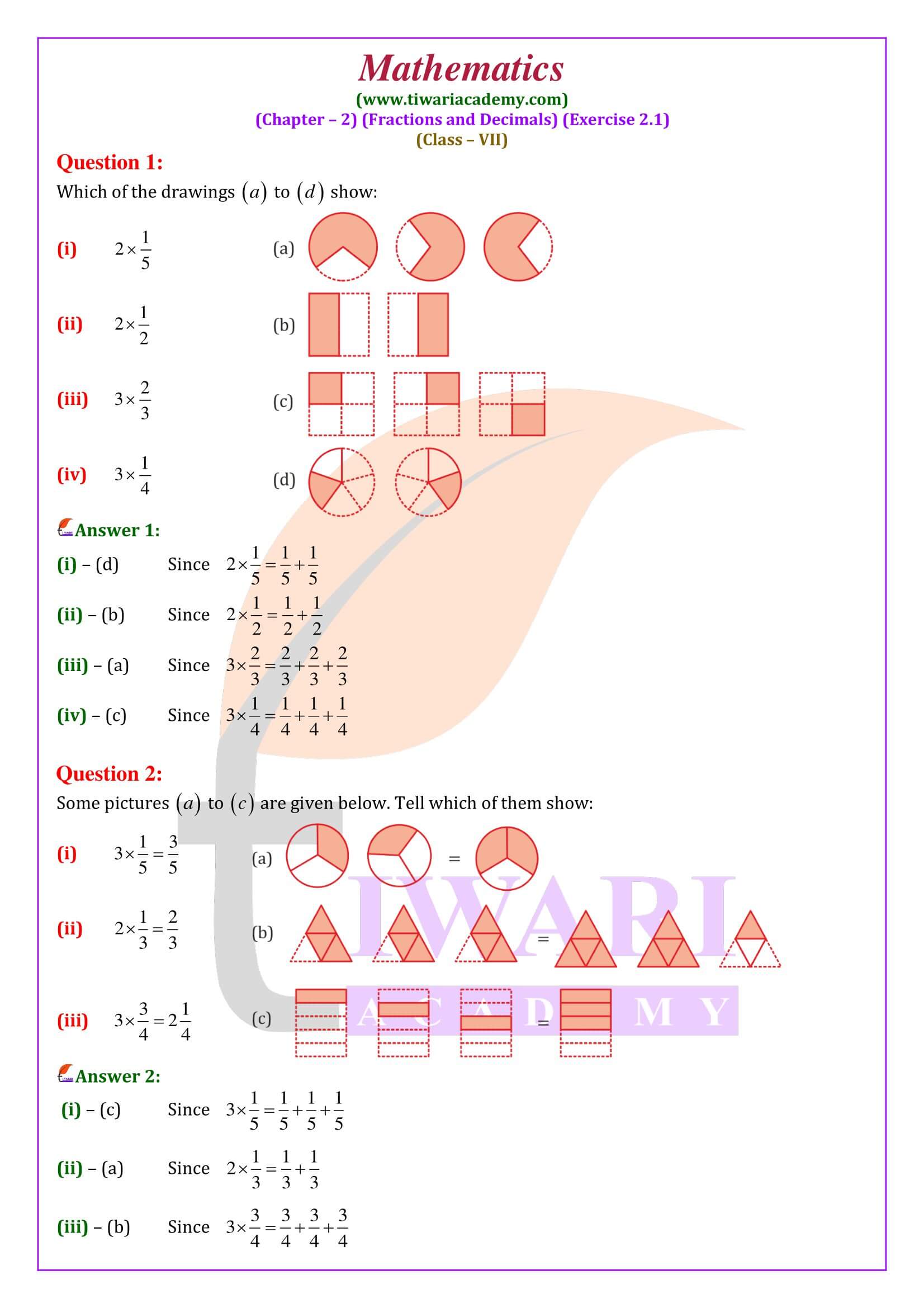
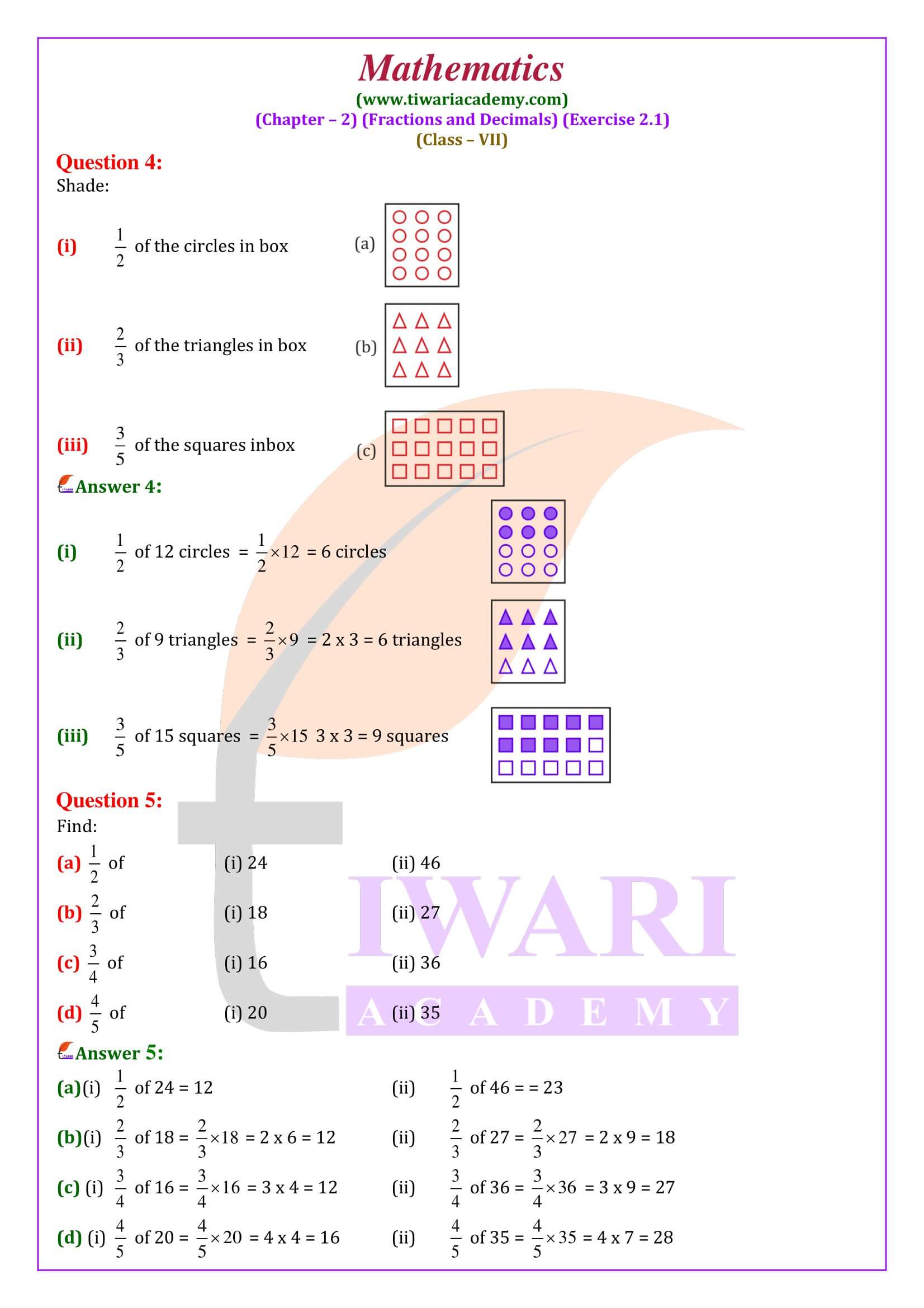
NCERT Solutions for Class 7 Maths Chapter 2 Exercise 2.1 Fractions and Decimals in Hindi and English Medium modified and updated for session 2024-25 according to CBSE and State board. Students of class 7 can take help to understand the solutions of ex. 2.1 mathematics based on new curriculum 2024-25.
NCERT Solutions Class 7 Maths Exercise 2.1 Solution in Hindi and English Medium
Class 7 Maths Chapter 2 Exercise 2.1 Solution
All the contents are solved step by step procedure using easier method. In class 7 math exercise 2.1 we practice the questions of fraction using pictures. Here we will also learn to convert mixed fraction to improper and improper to mixed fraction.
| Class: 7 | Mathematics |
| Chapter: 2 | Exercise: 2.1 |
| Topic Name: | Fractions and Decimals |
| Content: | Text, PDF and Videos Solution |
| Academic Year: | 2024-25 |
| Medium: | Hindi and English Medium |
Method of Changing Unlike Fractions to Like Fractions
Step 1. Find the LCM of the denominators of all the given fractions.
Step 2. Change each of the given fractions into an equivalent fraction having denominator equal to the LCM of the denominators of the given fractions.
Class 7 Maths Exercise 2.1 Practice Questions
Convert the fractions 5/6, 7/9, 11/12 into like fractions.
LCM of 6, 9, 12 = (3 x 2 x 3 x 2) = 36.
Now, 5/6 = (5 x 6)/ (6 x 6) = 30/36
7/9 = (7 x 4)/ (9 x 4) = 28/36
11/12 = (11 x 3)/ (12 x 3) = 33/36
Clearly, 30/36, 28/36, 33/36 are like fractions.
Convert 84/98 into irreducible form.
First we find the HCF of 84 and 98.
Clearly. HCF of 84 and 98 is 14.
So, we divide the numerator and denominator of the given fraction by 14.
So, 84/98 = (84/14)/ (98/14) = 6/7
Hence, 84/98 in irreducible form is 6/7.
Compare the fractions: (i) 3/5, 5/8 (ii) 9/16, 13/24
(i) By cross multiplication, we have:
3 x 8 = 24 and 5 x 5 = 25.
But, 24 < 25.
So, 3/5 < 5/8
(ii) By cross multiplication, we have:
9 x 24 = 216 and 16 x 13 = 208.
But, 216 > 208
So, 9/16 > 13/24
Arrange the factions 2/5, 3/10, 9/14, 16/35 in ascending order.
The given fractions are 2/5, 3/10, 9/14, 16/35
LCM of 5, 10, 14, 35 = (5 x 2 x 7) = 70.
Now, let us change each of the given fractions into an equivalent fraction having 70 as its denominator.
Now, 2/5 = (2 x 14)/ (5 x 14) = 28/70
3/10 = (3 x 7)/ (10 x 7) = 21/70
9/14 = (9 x 5)/ (14 x 5) = 45/70
16/35 = (16 x 2)/ (35 x 2) = 32/70
21/70 < 28/70 < 32/70 < 45/70
Hence, the given fractions in ascending order are 3/10 < 2/5 < 16/35 < 9/14
(ix) Irreducible fractions:
A fraction a/b is said to be irreducible or in lowest terms, if HCF of a and b is 1. If HCF of a and b is other than 1 than a/b is said to be reducible.
Comparing Fractions
Let a/b and c/d be two given fraction. Then,
(i) a/b > c/d or ad > bc
(ii) a/b = c/d or ad = bc
(iii) a/b < c/d or ad < bc
Class 7 Maths Exercise 2.1 Important Questions
How do you add a whole number and a fraction?
To add mixed numbers, we first add the whole numbers together, and then the fractions. …
If the denominators of the fractions are different, then first find equivalent fractions with a common denominator before adding.
How do you solve fraction addition problems?
Step 1: Make sure the bottom numbers (the denominators) are the same. Step
2: Add the top numbers (the numerators), put that answer over the denominator. Step
3: Simplify the fraction (if needed)
How do you add mixed fractions step by step?
The steps are the same whether you’re adding or subtracting mixed numbers:
Find the Least Common Denominator (LCD)
Find the equivalent fractions.
Add or subtract the fractions and add or subtract the whole numbers.
Write your answer in lowest terms.
Method of Comparing More Than Two Fractions
Step 1. Find the LCM of the denominators of the given fractions. Let it be m.
Step 2. Convert all the given fractions into like fractions, each having m as denominator.
Step 3. Now, if we compare any two of these like fractions, then the one having larger numerator is larger.
Addition and Subtraction of Fractions
Addition of Fractions
Rule 1. For adding two like fractions, the numerators are added and the denominator remains the same.
Examples:
(i) 2/9 + 5/9 = (2 + 5)/9 = 7/9
(ii) 8/15 + 6/15 = (8 + 6)/15 = 14/15
Rule 2. For addition of two unlike fractions. first change them to like fractions and then add them as given in Rule 1.
Example: add 3/10 + 8/15
LCM of 10 and 15 = (5 x 2 x 3) = 30.
So, 3/10 = (3 x 3)/ (10 x 3) = 9/30 and 8/15 = (8 x 2)/ (15 x 2) = 16/30
Now, 9/30 + 16/30 = 25/30 = 5/6
Properties of Addition of Fractions
(i) Addition of fractions is associative, i.e., (a/b + c/d) + e/f = a/b + (c/d + e/f)
(ii) Addition of fractions is commutative, i.e., (a/b + c/d) = (c/d = a/b)
Which sums of exercise 2.1 of class 7th Maths can students expect in Half-yearly exams?
In exercise 2.1 of class 7th Maths, there are eight questions and one example (Example 5). All sums of exercise 2.1 of class 7th Maths are significant. From this exercise, any question can come in the Half-yearly exams. Students should practice all sums of this exercise to score good marks in the Half-yearly exam.
Which concepts are introduced in exercise 2.1 of grade 7th Maths?
The concepts that are introduced in exercise 2.1 of grade 7th Maths are:
1. Multiplication of Fractions.
a. Multiplication of a Fraction by a Whole Number.
b. Fraction as an operator ‘of’ (‘of’ represents multiplication).
How many days are required to prepare exercise 2.1 of grade 7th Maths?
If all the concepts of exercise 2.1 of grade 7th Maths are clear to the students, then students require only two days (at least 2 hours per day) to prepare exercise 2.1 of grade 7th Maths. This time can increase or decrease depending on the student’s efficiency, working speed, etc.
Is exercise 2.1 of 7th standard Maths short?
Yes, exercise 2.1 of grade 7th Maths is short. It is not a lengthy exercise. Only eight questions and one example (example 5) are there in exercise 2.1 of Maths 7th Standard. Students find some questions of this exercise a little difficult and some questions simple.