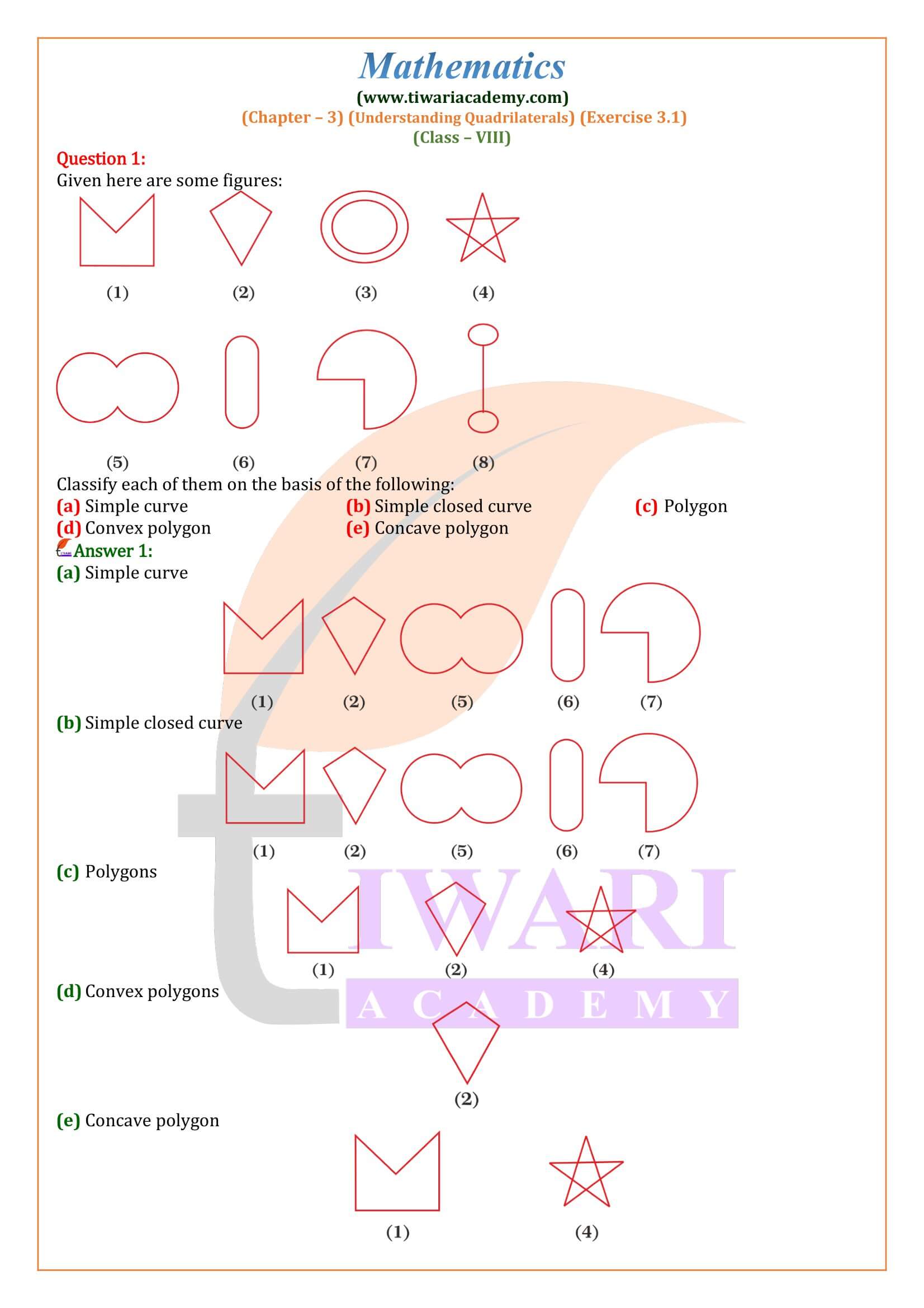
Class 8 Maths Exercise 3.1 Solutions
Class 8 Maths Exercise 3.1 in Hindi
Class 8 Maths Book Download in PDF
Class 8 Maths Chapter 3 Solutions
Class 8 Maths NCERT Solutions
Class 8 All Subjects Solutions
Get here modified NCERT Solutions for Class 8 Maths Chapter 3 Exercise 3.1 in Hindi and English Medium updated for 2025-26 Exams. The revised solutions of ex. 3.1 class 8th Maths are based on new NCERT textbooks issued for academic session 2025-26.
8th Maths Exercise 3.1 Solution in Hindi and English Medium
Class 8 Maths Chapter 3 Exercise 3.1 Solution
Class VIII Mathematics NCERT textbook Ex. 3.1 of chapter 3 Understanding Quadrilaterals in Hindi and English Medium updated for academic session 2025-26. Students can use exercise 3.1 solution online or download in PDF file format to use offline. Videos related to 8th Maths ex. 3.1 is given here with solution and explanation. All the questions are done step by step procedure one the basis of latest NCERT Book method.

| Class: 8 | Mathematics |
| Chapter: 3 | Exercise: 3.1 |
| Chapter Name: | Understanding Quadrilaterals |
| Content Type: | Images, Videos and Text Format |
| Medium: | Hindi and English Medium |
| Academic Session: | 2025-26 |
Polygon
A polygon is a flat shape made up of straight lines segments, that are connected to each other end to end to form a closed figure.
Polygons are two types:
- (i) Regular polygon
- (ii) Irregular polygon
Regular polygon
A polygon having all sides equal and all angles equal is called regular polygon. An equilateral triangle and a square are examples of regular polygons.
Irregular polygon
Polygons which are not regular are called irregular polygons. A rectangle and a rhombus are examples of irregular polygons.
Class 8 Maths Exercise 3.1 Important Questions
Find the value of each exterior angle of a regular polygon of: (i) 8 sides (ii) 9 sides (iii) 12 sides.
(i) Each exterior angle of a regular polygon of 8 sides = (360/8)0 = 45°.
(ii) Each exterior angle of a regular polygon of 9 sides = (360/9)0 = 40°.
(iii) Each exterior angle of a regular polygon of 12 sides = (360/12)0 = 30°.
Is it possible to have a regular polygon each of whose exterior angles is 25°?
Let the number of sides of the given polygon be n.
each of its exterior angles = (360/n)0
Now, 360/n = 25, so, n = 360/25 = 72/5, which is not a whole number.
So, it not possible to have a regular polygon each of whose exterior angles is 25.
Find the measure of each interior angle of a regular. (i) pentagon (ii) hexagon (iii) octagon (iv) polygon of 12 sides.
(i) Each exterior angle of a regular pentagon = (360/5)0 = 720.
Each of its interior angles = (180° – 72°) = 108°
(ii) Each exterior angle of a regular hexagon = (360/6)0 = 60°
Each of its interior angles = (180° – 60°) = 120°
(iii) Each exterior angle of a regular octagon = (360/6)0 = 45°
Each of its interior angles = (180° – 45°) = 135°.
(iv) Each exterior angle of a regular polygon of 12 sides = (360/6)0 = 30°.
Each of its interior angles = (180° – 30°) = 150°.
For a regular polygon of n sides, we have
(i) each exterior angle = (3600 /n)
(ii) each interior angle = 180° – (each exterior angle).
In a convex polygon of n sides, we have
(i) sum of all exterior angles = 4 right’s.
(ii) sum of all interior angles = (2n – 4) right’s.
Number of diagonals in a polygon of n sides = n(n – 3)/ 2.
Class 8 Maths Exercise 3.1 Extra Questions for Practice
What is the minimum interior angle possible for a regular polygon?
As the number of sides of a regular polygon decreases, each of its exterior angles increases and therefore each interior angle decreases. Thus, an equilateral triangle will have minimum interior angle, which is 60°.
What is the maximum exterior angle possible for a regular polygon?
As the number of sides of a regular polygon decreased, each of its exterior angles increases. So, it maximum in case of an equilateral triangle, which is 120°.
What is the number of diagonals in a (i) quadrilateral (ii) pentagon (iii) hexagon (iv) polygon of 10 sides?
Number of diagonals of n side = {n (n – 3)/2}
(i) Number of diagonals of a quadrilateral = {4 (4 – 3)/2} = (2 x 1) = 2.
(ii) Number of diagonals of a pentagon = {5 (5 – 3)/2} = (5 x 2)/2 = 5.
(iii) Number of diagonals of a hexagon = {6 (6 – 3)/2} = (6 x 3)/2 = 9.
(iv) Number of diagonals in a polygon 10 sides = {10 (10 – 3)/2} = (10 x 7)/2 = 35.
Find the number of sides of a regular polygon whose each exterior angle measure 45°.
Sum of all exterior angles of a regular polygon = 360°.
Each exterior angle = 45°
number of exterior angles = 360/45 = 8.
number of sides in the given polygon = 8.
concave polygon
A concave polygon is defined as a polygon with one or more interior angles greater than 180°. A concave polygon is the opposite of a convex polygon.
Different Types of Polygons
| Number of sides | Polygon Name |
|---|---|
| Three | Trigon or Triangle |
| Four | Tetragon or Quadrilateral |
| Five | Pentagon |
| Six | Hexagon |
| Seven | Heptagon |
| Eight | Octagon |
| Nine | Nonagon or Enneagon |
| Ten | Decagon |