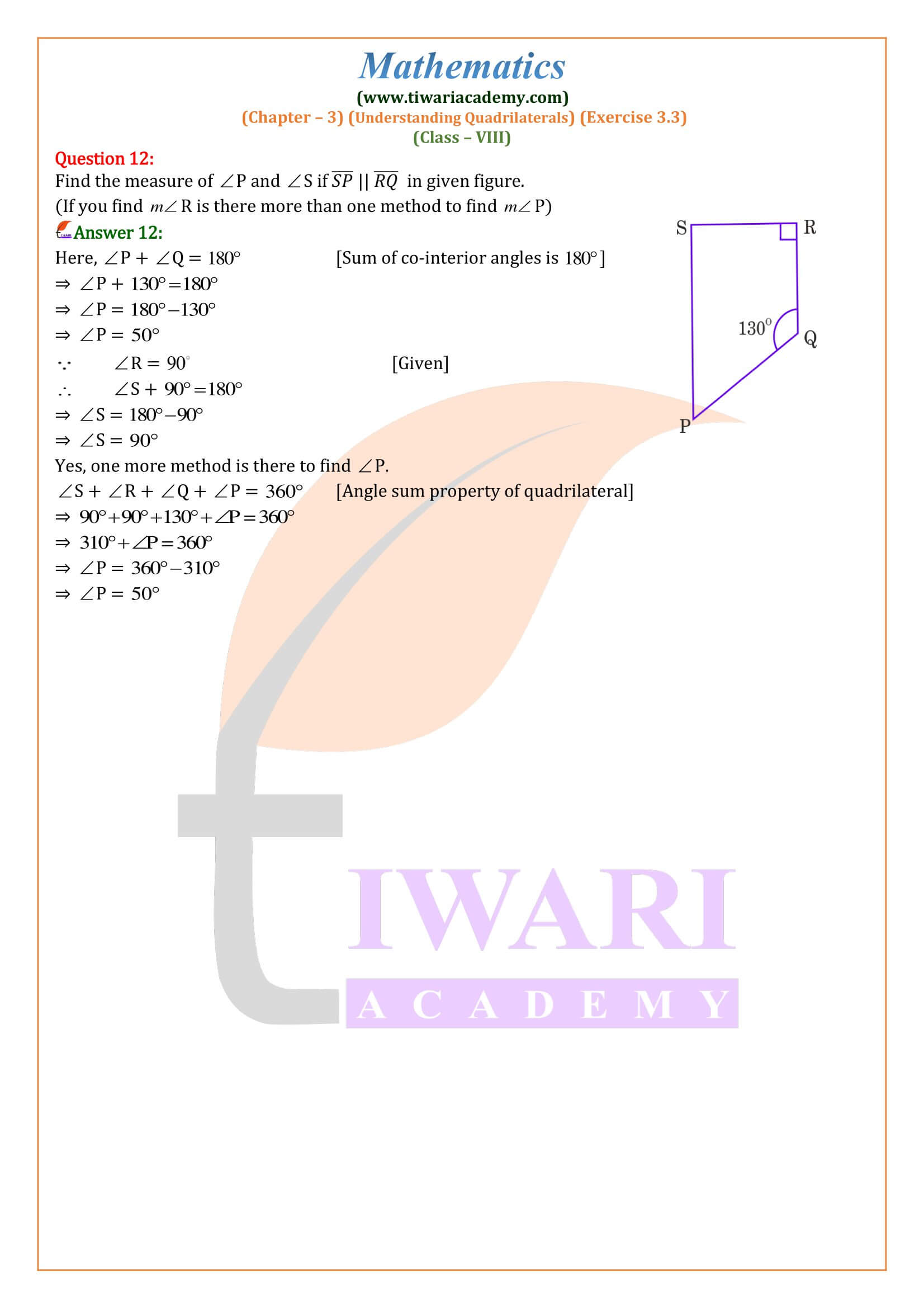
Class 8 Maths Exercise 3.3 Solutions
Class 8 Maths Exercise 3.3 in Hindi
Class 8 Maths Book Download in PDF
Class 8 Maths Chapter 3 Solutions
Class 8 Maths NCERT Solutions
Class 8 All Subjects Solutions
NCERT Solutions for Class 8 Maths Chapter 3 Exercise 3.3 in Hindi and English Medium revised and updated for new session 2024-25. The solutions of ex. 3.3 class VIII mathematics are modified on the basis of new NCERT textbooks issued for 2024-25 examination.
Class VIII Mathematics NCERT Ex. 3.3 of chapter 3 Understanding Quadrilaterals in Hindi and English Medium updated for academic session 2024-25. Here we have to learn about the properties of quadrilateral and their internal angles along with angle sum property of quadrilateral based question. All the questions are solved with easy method, according to standard 8 NCERT Book. Videos related to 8th mathematics ex. 3.3 also helps a lot during the practice.
8th Maths Exercise 3.3 Solution in Hindi and English Medium

| Class: 8 | Mathematics |
| Chapter: 3 | Exercise: 3.3 |
| Chapter Name: | Understanding Quadrilaterals |
| Content: | Text and Videos Online |
| Medium: | Hindi and English Medium |
| Academic Session: | 2024-25 |
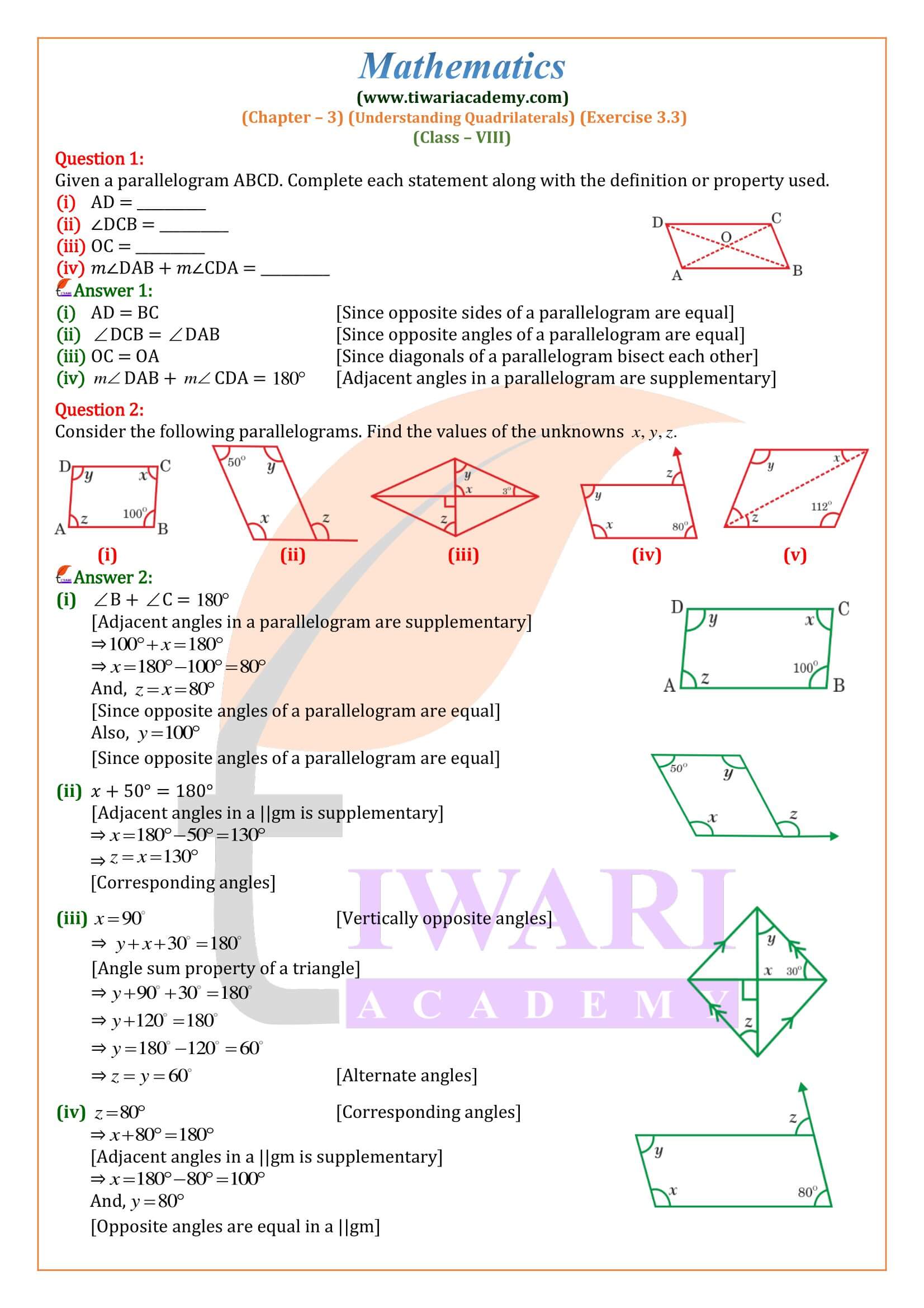
Parallelogram:
A quadrilateral is called a parallelogram if both pairs of its opposite sides are parallel. ABCD is a quadrilateral in which AB || DC and AD || BC.
So, ABCD is parallelogram.
Rhombus
A parallelogram having all sides equal is called a rhombus. ABCD is a rhombus in which
AB || DC, AD || BC and AB = BC = CD = DA
Rectangle
A parallelogram in which each angle is a right angle is called a rectangle. ABCD is a quadrilateral in which AB || DC, AD || BC
and ∠A = ∠B = ∠C = ∠D = 90°. So, ABCD is a rectangle.
Square
parallelogram in which all the sides are equal each angle measures 90° is called a square. ABCD is a quadrilateral in which AB || DC, AD || BC, AB = BC = CD = DA and ∠A = ∠B = ∠C = ∠D = 90°. So, ABCD is a square.
Kite
A quadrilateral is called a kite if it has two pairs of equal adjacent sides but unequal opposite sides. In the adjoining figure, ABCD is a quadrilateral in which AB = AD, BC = DC, AD ≠ BC and AB = DC. So, ABCD is a kite.
Class 8 Maths Exercise 3.3 Important Questions
Prove that any two adjacent angles of a parallelogram are supplementary.
Let ABCD be a parallelogram. Then, AD || BC and AB is a transversal.
So, ∠A + ∠B = 180°, [ sum of interior angles on the same side if the transversal is 180°]
Similarly,
∠B + ∠C = 1800, ∠C + ∠D = 1800 and ∠D + ∠A = 180°.
Thus, the sum of any two adjacent angles of a parallelogram is 180°.
Hence, any two adjacent angles of a parallelogram are supplementary.
The ratio of two sides of a parallelogram is 4 :3 If its perimeter is 56 cm, find the lengths of its sides.
Let the lengths of two sides of the parallelogram be 4x cm and 3x cm respectively.
The, its perimeter = 2 (4x + 3x) cm = 14x cm. 14x = 56 x = 4
one side = (4 x 4) cm = 16 cm and other side = (3 x 4) cm = 12 cm.
Properties of a Parallelogram
Prove that in a parallelogram
- (i) The opposite sides are equal;
- (ii) The opposite angles are equal;
- (iii) Diagonals bisect each other.
Class 8 Maths Exercise 3.3 Extra Questions for Practice
What makes a parallelogram special?
Properties of a Parallelogram
Parallelograms are quadrilaterals that have two sets of parallel sides and two sets of congruent sides. A parallelogram’s opposite angles are congruent; its consecutive angles are supplementary; its diagonals bisect each other and its diagonals form two congruent triangles.
Is diagonal of parallelogram equal?
The diagonals of a parallelogram are equal. The opposite sides and opposite angles of a parallelogram are equal. And these opposite sides and angles make up for two congruent triangles, with the two diagonals being the sides of these two congruent triangles. Hence the diagonals of the parallelogram are equal.
A square is a parallelogram. This i
Is a parallelogram a square?s always true. Squares are quadrilaterals with 4 congruent sides and 4 right angles, and they also have two sets of parallel sides. Parallelograms are quadrilaterals with two sets of parallel sides.
PROOF
Let ABCD be a parallelogram. Draw its diagonals AC. In DABC and DCDA, we have:
∠1 = ∠4 (alternate angles) ∠3 = ∠2 (alternate angles) and AC = CA (common)
DABC congruent DCDA (by ASA congruence) AB = CD, BC = DA and ∠B = ∠D.
Similarly, by drawing the diagonal BD, we can prove that triangle ABD congruent triangle CDB.
∠A = ∠C Thus, AB = CD, BC = DA, B = D and A = C.
This proves (i) and (ii).
In order to prove (iii) consider parallelogram ABCD and draw its diagonals AC and BD, intersecting each other at O.
In triangle OAB and triangle OCD, we have AB = CD (opposite sides of a parallelogram)
∠AOB = ∠COD (vertically opposite angles)
∠OAB = ∠OCD (alternate angles)
triangle OAB = triangle OCD (by ASA property)
OA = OC and OB = OD.
This shows that the diagonals of a parallelogram bisect each other.
This converse of the above result is also true, i.e.,
- A quadrilateral is a parallelogram if its opposite sides are equal.
- A quadrilateral is a parallelogram if its opposite angles are equal.
- A quadrilateral is a parallelogram if its diagonals bisect each other.
Remark:
A rectangle, a square and a rhombus are special types of parallelogram. So, all the properties of a parallelogram are satisfied by each one of them.
1. In a parallelogram:
(i) opposite sides are equal
(ii) opposite angles are equal
(iii) diagonals bisect each other.
2. Quadrilateral as a Parallelogram
(i) If the opposite sides of a quadrilateral are equal then it is a parallelogram
(ii) If the opposite angles of a quadrilateral are equal then it is a parallelogram
(iii) If the diagonals of a quadrilateral bisect each other then it is a parallelogram