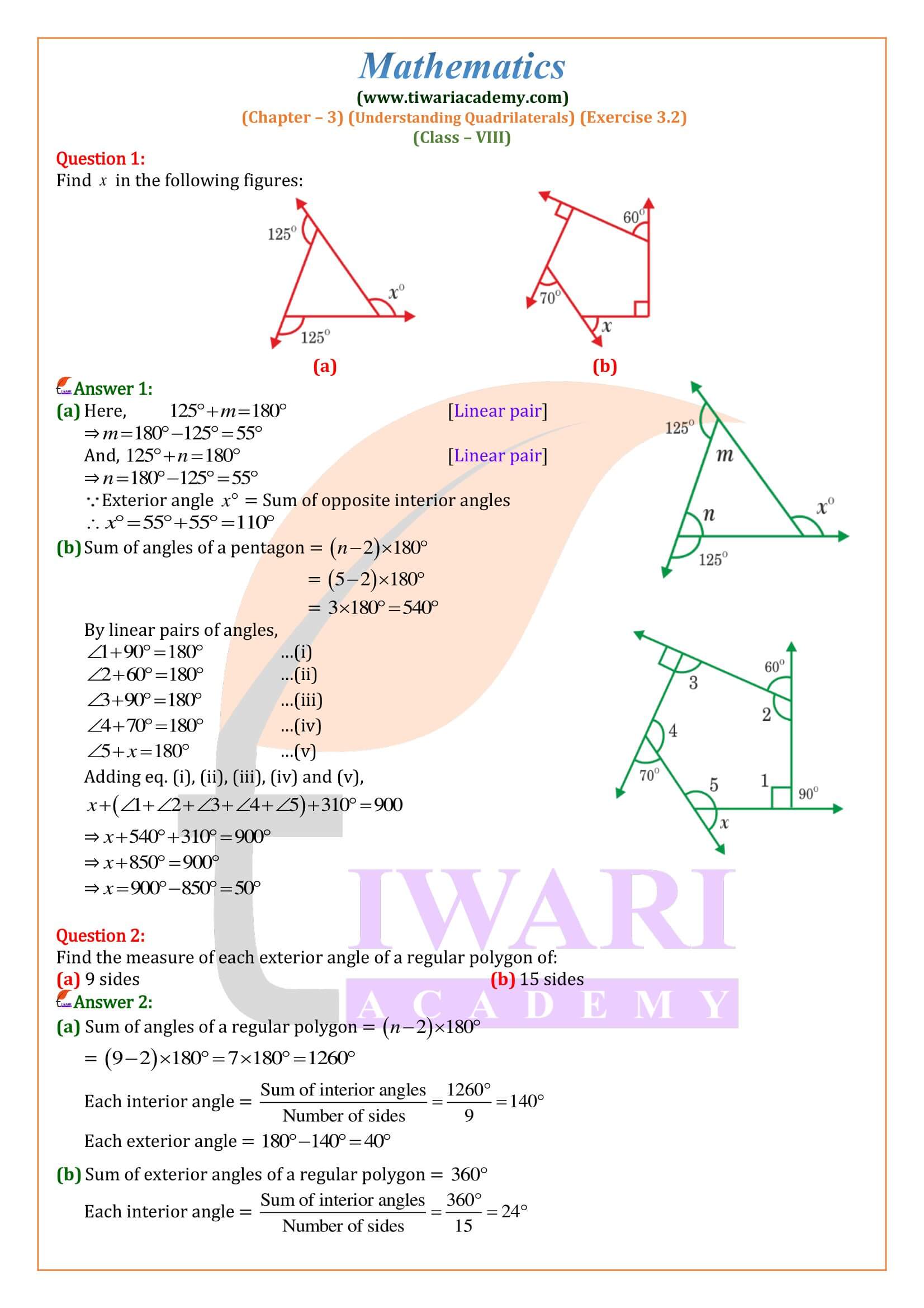
Class 8 Maths Exercise 3.2 Solutions
Class 8 Maths Exercise 3.2 in Hindi
Class 8 Maths Book Download in PDF
Class 8 Maths Chapter 3 Solutions
Class 8 Maths NCERT Solutions
Class 8 All Subjects Solutions
NCERT Solutions for Class 8 Maths Chapter 3 Exercise 3.2 in Hindi and English Medium modified and updated for academic year 2025-26. The question answers and explanations of ex. 3.2 of 8th Maths are revised according to new syllabus and revised NCERT books for 2025-26 exams.
8th Maths Exercise 3.2 Solution in Hindi and English Medium
Class 8 Maths Chapter 3 Exercise 3.2 Solution
Class VIII Mathematics NCERT book Ex. 3.2 of chapter 3 Understanding Quadrilaterals in PDF file format free to download or use online without downloading. All the solutions of questions in exercise 3.2 of class 8 mathematics are done properly step by step. We have provided the CBSE solutions in simple way with best way of solution and easy to understand. If anyone face problem during the use of NCERT Solution App or website call us for without any hesitation.

| Class: 8 | Mathematics |
| Chapter: 3 | Exercise: 3.2 |
| Chaper Name: | Understanding Quadrilaterals |
| Content: | NCERT Book Solution |
| Medium: | Hindi and English Medium |
| Academic Session: | 2025-26 |
Area of Polygon
A closed figure bounded by three or more line segments is called a polygon. A polygon is said to be regular, if it is both ‘equiangular’ and ‘equilateral’. A polygon is named according to the number of sides it contains.
| Name of the polygon | Number of sides |
|---|---|
| Quadrilateral | 4 |
| Pentagon | 5 |
| Hexagon | 6 |
| Heptagon | 7 |
| Octagon | 8 |
Similarly, nine-sided figure is called nonagon and ten-sided figure is called decagon.
In a quadrilateral ABCD
- (i) The four points A, B, C, D are called its vertices,
- (ii) The four line segments AB, BC, CD, and DA are called its sides,
- (iii) ∠DAB, ∠ABC, ∠BCD and ∠CDA are called its angles to be denoted by ∠A, ∠B, ∠C and ∠D respectively, and
- (iv) The line segments AC and BD are called its diagonals.
Adjacent Sides of a Quadrilateral
Two sides of a quadrilateral which have a common end point are called its adjacent sides. In the given figure, (AB, BC), (BC, CD), (CD, DA) and (DA, AB) are four pairs of adjacent sides of quad. ABCD.
Opposite Sides of a Quadrilateral
Two sides of a quadrilateral are called its opposite sides if they do not have a common end point.
In the given figure, (AB, DC) and (AD, BC) are two pairs of opposite sides of quad. ABCD.
Adjacent Angles of a Quadrilateral
Two angles of a quadrilateral having a common arm are called its adjacent angles. Opposite Angles of a Quadrilateral Two angles of a quadrilateral which are not adjacent angles are known as opposite angles. In the given figure, (∠A, ∠C) and (∠B, ∠D) are two pairs of opposite angles of quad. ABCD.
In the given figure, (∠A, ∠B), (∠B, ∠C), (∠C, ∠D) and (∠D, ∠A) are four pairs of adjacent angles of quad. ABCD.
Angle Sum property of Quadrilateral
Prove that the sum of angles of a quadrilateral is 360°.
Proof:
Let ABCD be a quadrilateral, Join AC.
Clearly, ∠1 + ∠2 = ∠A … (i)
And, ∠3 + ∠4 = ∠C … (ii)
We know that the sum of the angles of a triangle is 180°.
So, from triangle ABC, we have ∠2 + ∠4 + ∠B = 180°.
From triangle ACD, we have ∠1 + ∠3 + ∠D = 180°.
Adding the angles on either side, we get:
∠2 + ∠4 + ∠B + ∠1 + ∠3 + ∠D = 360°.
Or, (∠1 + ∠2) + ∠B + (∠3 + ∠4) + ∠D = 360°.
Or, ∠A + ∠B + ∠C + ∠D = 360° [using (i) and (ii)].
Hence, the sum of the angles of a quadrilateral is 360°.
Class 8 Maths Exercise 3.2 Important Questions
Three angles of a quadrilateral are 54°, 80° and 116°. Find the measure of the fourth angle.
Let the measure of the fourth angle be x°.
We know that the sum of the angles of a quadrilateral is 360°.
So, 54 + 80 + 116 + x = 360
Or, 250 + x = 360
Or, x = (360 – 250) = 110.
Hence, the measure of the fourth angle is 110°.
The four angles of a quadrilateral are in the ratio 2 : 3 : 5 : 8. Find the angles.
Let the measure of the angles given quadrilateral be (2x)°, (3x)°, (5x)° and (8x)°.
We know that the sum of the angles of a quadrilateral is 360°.
So, 2x + 3x + 5x + 8x = 360
Or, 18x = 360
Or, x = 20.
So, the values of angles of the given quadrilateral are (2 x 20)°, (3 x 20)°, (5 x 20)° and (8 x 20)° i.e., 40°, 60°, 100° and 160°.
The measure of two angles of a quadrilateral 115° and 45°, and the other two angles are equal. Find the measure of each of the equal angles.
Let the measure of each of the equal angles be x°.
We know that the sum of all the angles of a quadrilateral is 360°.
So, 115 + 45 + x + x = 360.
Or, 160 + 2x = 360
Or, 2x = (360 – 160) = 200
Or, x = 100.
Hence, the measure of each of the equal angles is 100°.
Properties of Quadrilaterals:
Parallelograms
- Opposite sides of a parallelogram are congruent.
- Opposite angles of a parallelogram are congruent.
- Consecutive angles in a parallelogram are supplementary.
- The diagonals of a parallelogram bisect each other.
Rectangles
- 1) Opposite sides are congruent (they equal each other).
- 2) Opposite angles are congruent (they equal each other).
- 3) Consecutive angles are supplementary (they add up to 180).
- 4) Diagonals bisect each other (the parts are equal).
- 5) Diagonals are congruent (they equal each other).
- 6) All four corner angles are 90°.
Squares
- 1) Opposite sides are congruent (they equal each other).
- 2) Opposite angles are congruent (they equal each other).
- 3) Consecutive angles are supplementary (they add up to 180).
- 4) Diagonals bisect each other (the parts are equal).
- 5) Diagonals are congruent (they equal each other).
- 6) All four corner angles are 90°.
- 7) Diagonals perpendicular (the form right angles in the middle).
- 8) Diagonals bisect angles (the angles equal to each other).
Rhombus
- Opposite sides are congruent (they equal each other).
- Opposite angles are congruent (they equal each other).
- Consecutive angles are supplementary (they add up to 180).
- Diagonals bisect each other (the parts are equal).
- Diagonals perpendicular (the form right angles in the middle).
- Diagonals bisect angles (the angles are equal to each other).
- All four sides are congruent.
- The diagonals are NOT congruent.
Class 8 Maths Exercise 3.2 Extra Questions for Practice
What is quadrilateral?
As the word ‘Quad’ means four, all these types of a quadrilateral have four sides, and the sum of angles of these shapes is 360 degrees.
What is the properties of a quadrilateral?
Opposite angles are equal. All sides are equal and, opposite sides are parallel to each other. Diagonals bisect each other perpendicularly. Sum of any two adjacent angles is 180°
How many diagonals does a quadrilateral have?
A quadrilateral, the next-simplest, has two diagonals. A pentagon, whether regular or irregular, has five diagonals. In convex, simple polygons, diagonals will always be within the interior.
What is a vertex of a quadrilateral?
A point where any two edges of a quadrilateral meet, is called a vertex of a quadrilateral.
Isosceles Trapezoids
1) Lower two base angles are congruent (they equal each other).
2) Upper two base angles are congruent (they equal each other).
3) The diagonals are congruent (they equal each other).
4) opposite angles are supplementary (they add up to 180).
Kite
- 1) Two pairs of consecutive sides congruent, but opposite sides not congruent
- 2) Diagonals perpendicular.
- 3) Exactly one pair of angles congruent.
- 4) One pair of angles bisected.