NCERT Solutions for Class 8 Maths Ganita Prakash Chapter 3 A Story of Numbers

Page 54

Figure it Out

1. Suppose you are using the number system that uses sticks to represent numbers, as in Method 1. Without using either the number names or the numerals of the Hindu number system, give a method for adding, subtracting, multiplying and dividing two numbers or two collections of sticks.
See SolutionMethod 1: Addition (Putting Together)
► Collect sticks representing the first quantity.
► Collect another set of sticks representing the second quantity.
► Combine both sets into a single group.
► The total number of sticks in the combined group represents the sum.
Example:
Group A: |||| (4 sticks)
Group B: ||| (3 sticks)
Total: ||||||| (7 sticks)
Method 2: Subtraction (Taking Away)
► tart with the group of sticks representing the larger collection.
► Remove or take away the number of sticks that represent the smaller quantity.
► The remaining sticks show the result of subtraction.
Example:
Start with: ||||||| (7 sticks)
Take away: ||| (3 sticks)
Left: |||| (4 sticks)
Method 3: Multiplication (Repeated Addition)
► Make several groups of sticks, each containing the same number.
► Count all the sticks across all groups together.
► The total represents the product.
Example:
Multiply 3 groups of ||| (3 sticks each):
Group 1: |||
Group 2: |||
Group 3: |||
Total: ||||||||||| (9 sticks)
Method 4: Division (Equal Sharing or Grouping)
► Take the total number of sticks.
► Split them into equal groups.
Either:
• Count how many sticks are in each group (equal sharing), or
• Count how many such groups can be made (repeated subtraction).
Example (Equal Sharing):
Total: |||||| (6 sticks), divide into 2 groups → ||| and ||| (3 sticks each)
Example (Grouping):
How many groups of || (2 sticks) can be made from |||||| (6 sticks)?
Answer: 3 groups.

2. One way of extending the number system in Method 2 is by using strings with more than one letter — for example, we could use ‘aa’ for 27. How can you extend this system to represent all the numbers? There are many ways of doing it!
See SolutionTreat it like a base-26 system using letters.
Each letter acts like a digit and we treat sequences like base-26 numbers, where:
‘a’ = 1, ‘b’ = 2, …, ‘z’ = 26
After ‘z’, we continue with:
‘aa’ = 27
‘ab’ = 28 …
‘az’ = 52
‘ba’ = 53 …
‘zz’ = 26×26 = 676
‘aaa’ = 677
and so on …
Alternate methods:
► Repeating letters:
a = 1, b = 2, …, z = 26
aa = 27, bb = 28, … but this method runs out quickly and isn’t consistent.
► Insert separators:
After 26, start using combinations like ‘a-a’, ‘a-b’, ‘a-c’, etc.
But this is less efficient and harder to scale.
► Numeric suffix:
a1 = 1, a2 = 2, …, z1 = 26, a1a = 27, etc.
More complex but customizable.

3. Try making your own number system.
See SolutionMy Own Number System: The “ABC Number System”
• In this number system, I use the letters A, B, C, D and E instead of normal digits.
• Each letter stands for a number: A = 0, B = 1, C = 2, D = 3 and E = 4.
This means I can count using only these five letters, just like we normally count with digits 0 to 9 in the usual number system.
• I also follow place value — the rightmost letter is worth 1s, then 5s, then 25s, and so on (because this is a base-5 system).
For example, the code BD means B = 1 (in 5s place) and D = 3 (in 1s place). So BD = (1 × 5) + 3 = 8. This system is fun and feels like a secret code!
• I can count and do Maths using only letters, which helps me understand how numbers can be written in many different ways.

Page 59

Figure it Out

1. Represent the following numbers in the Roman system.
(i) 1222
See SolutionBreak into parts:
1000 + 200 + 20 + 2
= M + CC + XX + II
= MCCXXII

(ii) 2999
See SolutionBreak into parts:
1000 + 1000 + 900 + 90 + 9
= M + M + CM + XC + IX
= MMCMXCIX

(iii) 302
See SolutionBreak into parts:
300 + 2
= CCC + II
= CCCII

(iv) 715
See SolutionBreak into parts:
700 + 10 + 5
= DCC + X + V
= DCCXV

Page 60

Figure it Out

1. A group of indigenous people in a Pacific island use different sequences of number names to count different objects. Why do you think they do this?
See SolutionIndigenous people on a Pacific island might use different sequences of number names for different objects because their language and culture are closely connected to daily life and nature. They may count coconuts, fish, people or days differently because each object is important in a different way and may follow different traditions.
For example, they might use one type of number word for living things and another for non-living things or they may count pairs of items (like eyes or shoes) instead of single pieces. Using different number systems helps them understand, group and remember things more easily in their own way.

2. Consider the extension of the Gumulgal number system beyond 6 in the same way of counting by 2s. Come up with ways of performing the different arithmetic operations (+, –, ×, ÷) for numbers occurring in this system, without using Hindu numerals. Use this to evaluate the following:
(i) (ukasar-ukasar-ukasar-ukasar-urapon) + (ukasar-ukasarukasar-urapon)
(ii) (ukasar-ukasar-ukasar-ukasar-urapon) – (ukasar-ukasarukasar)
(iii) (ukasar-ukasar-ukasar-ukasar-urapon) × (ukasar-ukasar)
(iv) (ukasar-ukasar-ukasar-ukasar-ukasar-ukasar-ukasar-ukasar) ÷ (ukasar-ukasar)
See SolutionUnderstanding the Gumulgal number system, which counts in groups of 2 using the following number names:
urapon = 1
ukasar = 2
ukasar-urapon = 3 (2 + 1)
ukasar-ukasar = 4 (2 + 2)
ukasar-ukasar-urapon = 5 (2 + 2 + 1)
ukasar-ukasar-ukasar = 6 (2 + 2 + 2) and so on…
► Converting Gumulgal terms to Hindu numerals:
(ukasar-ukasar-ukasar-ukasar-urapon)
→ 2 + 2 + 2 + 2 + 1 = 9
(ukasar-ukasar-ukasar-urapon)
→ 2 + 2 + 2 + 1 = 7
(ukasar-ukasar)
→ 2 + 2 = 4
(ukasar-ukasar-ukasar-ukasar-ukasar-ukasar-ukasar-ukasar)
→ 8 ukasar = 8 × 2 = 16
► Performing Arithmetic Operations:
(i) Addition: 9 + 7 = 16
→ Convert 16 back into Gumulgal style:
8 ukasar → ukasar-ukasar-ukasar-ukasar-ukasar-ukasar-ukasar-ukasar
(ii) Subtraction: 9 – 6 = 3
→ 2 + 1 = ukasar-urapon
(iii) Multiplication: 9 × 4 = 36
→ Break 36 as 2 + 2 + 2 + … 18 times = 18 ukasar
→ ukasar-ukasar-ukasar-ukasar-ukasar-ukasar-ukasar-ukasar-ukasar-ukasar-ukasar-ukasar-ukasar-ukasar-ukasar-ukasar-ukasar-ukasar
(iv) Division: 16 ÷ 4 = 4
→ 2 + 2 = ukasar-ukasar

3. Identify the features of the Hindu number system that make it efficient when compared to the Roman number system.
See SolutionFeatures that Make the Hindu Number System Efficient than Roman number system:
• Uses a place value system where the position of a digit determines its value.
• Includes zero (0) as both a digit and a placeholder.
• Needs only 10 symbols (0–9) to represent any number.
• Allows for easy and quick arithmetic operations (addition, subtraction, etc.).
• Unambiguous and compact representation of even very large numbers.
• Forms the base for modern mathematics and science.
• Globally accepted and used in all fields today.

4. Using the ideas discussed in this section, try refining the number system you might have made earlier.
See SolutionAfter learning from this chapter, I improved my number system as follows:
► I improved my number system by making it a base-5 system.
► It uses five symbols: A, B, C, D, E (where A = 0, B = 1, …, E = 4).
► Each position from right to left represents powers of 5 (1, 5, 25, 125…).
► I added place value, so the same symbol has different values based on its position.
► Including A as zero helps avoid confusion and allows writing large numbers easily.
► This system is now more compact, clear and good for calculations, just like the Hindu number system.

Page 62

Figure it Out

1. Represent the following numbers in the Egyptian system: 10458, 1023, 2660, 784, 1111, 70707.
Answer:
Image

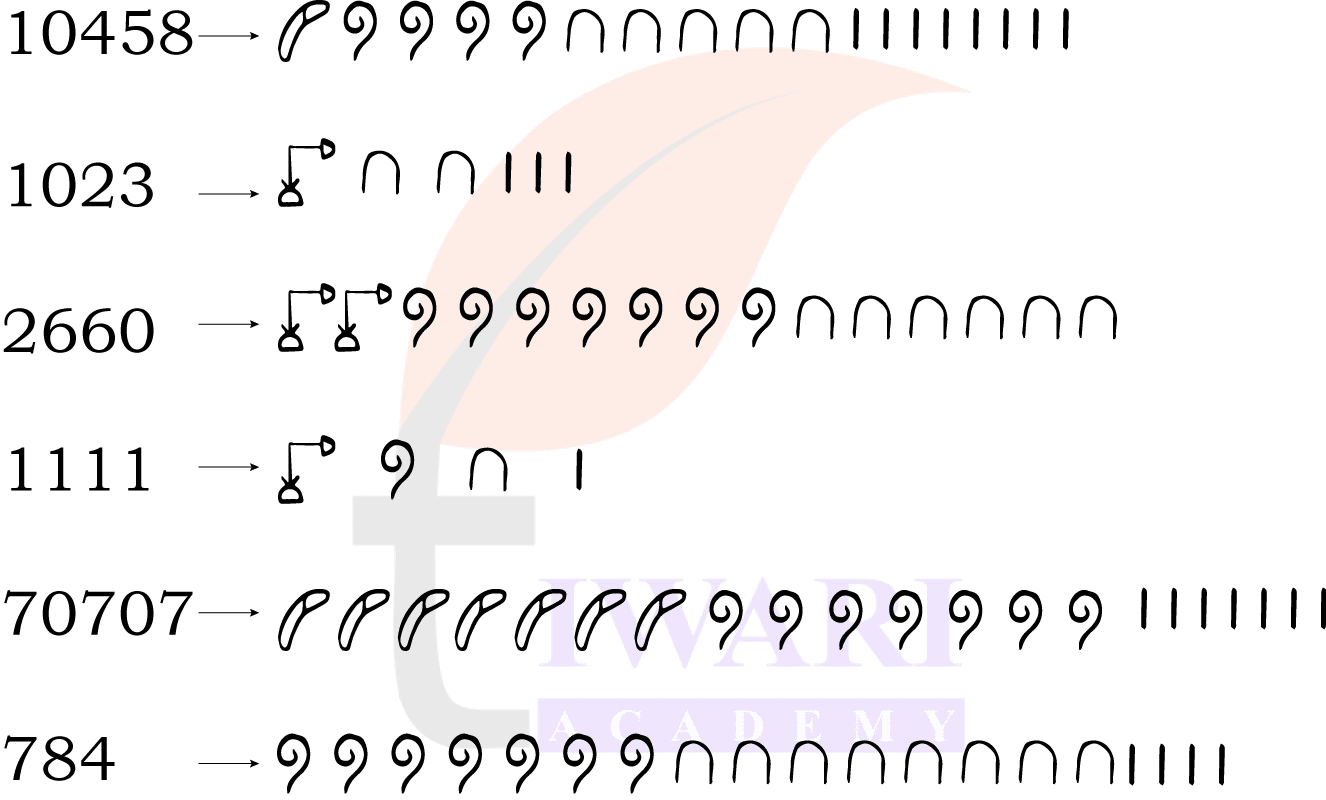
2. What numbers do these numerals stand for?

See Solution(i) 100 + 100 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 1 + 1 + 1 + 1 + 1 + 1
= 200 + 70 + 6
= 276
(ii) 1000 + 1000 + 1000 + 1000 + 100 + 100 + 100 + 10 + 10 + 1 + 1
= 4000 + 300 + 20 + 2
= 4322

Page 63

Figure it Out

1. Write the following numbers in the above base-5 system using the symbols in Table 2: 15, 50, 137, 293, 651.
Answer:

2. Is there a number that cannot be represented in our base-5 system above? Why or why not?
See SolutionNo, there is no number that cannot be represented in our base-5 system.
Because:
• A base-5 system uses digits A, B, C, D, E (which stand for 0 to 4).
• Any number, no matter how big, can be written using combinations of these symbols and place values based on powers of 5 (1, 5, 25, 125…).
• Since there is no upper limit on how many places we can use, we can represent every whole number.

3. Compute the landmark numbers of a base-7 system. In general, what are the landmark numbers of a base-n system?
See SolutionThe landmark numbers of a base-7 system:
In a base-7 system, the landmark numbers are powers of 7:
7⁰ = 1
7¹ = 7
7² = 49
7³ = 343
7⁴ = 2401
7⁵ = 16807
…and so on.
The landmark numbers of a base-n number system are the powers of n starting from n⁰ = 1, n, n², n³,…

Page 65

Figure it Out

1. Add the following Egyptian numerals:

Answer:

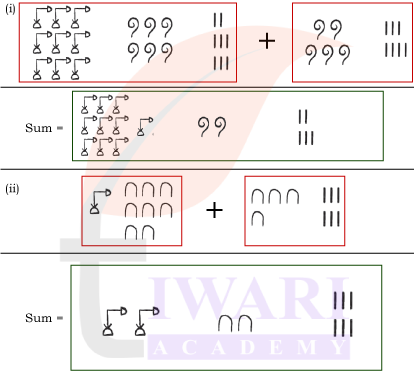
2. Add the following numerals that are in the base-5 system that we created:

Answer:

Page 69

Figure it Out

1. Can there be a number whose representation in Egyptian numerals has one of the symbols occurring 10 or more times? Why not?
See SolutionNo, there cannot be a number whose representation in Egyptian numerals has one of the symbols occurring 10 or more times.
Because:
• The Egyptian number system is an additive system, not a place value system.
• Symbols are repeated to add up values, but each symbol is used at most 9 times.
• The system had only a limited number of symbols, each of which was repeated no more than 9 times in writing any number.
So, whenever a symbol would be needed 10 times or more, Egyptians would move to the next higher symbol instead of repeating it, making their writing more compact and systematic.

2. Create your own number system of base 4 and represent numbers from 1 to 16.
See SolutionI have created my own number system called the Quad-Code System, which is based on base-4. In this system, I use four special symbols instead of regular digits:
A = 0
B = 1
C = 2
D = 3
In base-4, the place values increase as powers of 4. So, the rightmost place is 4⁰ = 1 =1, the next is 4¹ = 4 and then 4² = 16 and so on. Using this system, I can write any number using just these four symbols.
Here is how I write numbers from 1 to 16:
► 1 is written as B
► 2 is written as C
► 3 is written as D
► 4 is written as BA
► 5 is written as BB
► 6 is written as BC
► 7 is written as BD
► 8 is written as CA
► 9 is written as CB
► 10 is written as CC
► 11 is written as CD
► 12 is written as DA
► 13 is written as DB
► 14 is written as DC
► 15 is written as DD
► 16 is written as ABA

3. Give a simple rule to multiply a given number by 5 in the base-5 system that we created.
See SolutionThe simple rule to multiply a number by 5 in the base-5 system I created using symbols (A = 0, B = 1, C = 2, D = 3, E = 4):
Rule: Add a zero (A) at the end of the number
In base-5, multiplying any number by 5 is the same as shifting its digits one place to the left and adding A (zero) at the right end — just like adding a zero in base-10 when multiplying by 10.
Example:
Let’s say the number is BC (which is 1×5 + 2 = 7 in decimal)
Now multiply by 5 → just add A at the end → BCA
BCA in base-5 = 7 × 5 = 35 in decimal
Because in base-5, the digits shift just like in base-10. Adding a zero (A) multiplies the number by the base itself, i.e., 5.

Page 73

Figure it Out

1. Represent the following numbers in the Mesopotamian system —
(i) 63 (ii) 132 (iii) 200 (iv) 60 (v) 3605
Answer:

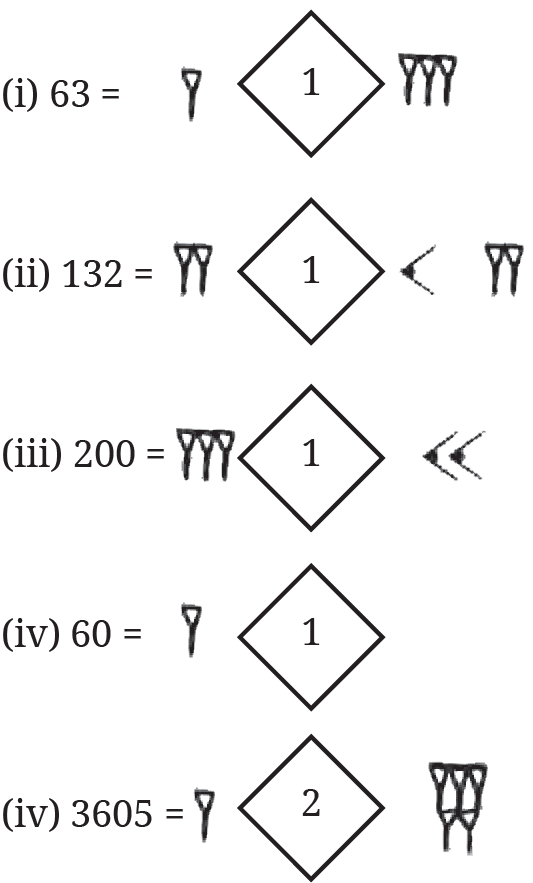
Page 80

Figure it Out

1. Why do you think the Chinese alternated between the Zong and Heng symbols? If only the Zong symbols were to be used, how would 41 be represented? Could this numeral be interpreted in any other way if there is no significant space between two successive positions?
See SolutionUsing Zong and Heng symbols:
• The Chinese number system used Zong (vertical) and Heng (horizontal) symbols to show place value clearly.
• They alternated the direction of the symbols at each place (units, tens, hundreds, etc.) to avoid confusion when reading the number.
• This made it easier to know which digit belonged to which place even when spaces were small or missing.
► If only Zong symbols were used, how would 41 be written?
In Chinese system: 41 = 4 tens and 1 unit.
Using only Zong symbols, it would be written as:
(Zong for 4) followed by (Zong for 1) → looks like: IIII I
Without alternating the symbol direction or keeping proper spacing: IIII I could be misread as 5 (i.e., 1 five) instead of 41.
The lack of direction or spacing removes the clue that one part is “tens” and the other is “units”.
► The Chinese alternated between Zong and Heng symbols to make place values visually clear and easy to read, especially in handwritten or closely packed texts. Without this, numbers like 41 could easily be misunderstood.

2. Form a base-2 place value system using ‘ukasar’ and ‘urapon’ as the digits. Compare this system with that of the Gumulgal’s.
See SolutionTo form a base-2 place value system using ‘ukasar’ and ‘urapon’, we assign:
• ‘ukasar’ = 0
• ‘urapon’ = 1
This system works just like the binary number system, where each position from right to left represents increasing powers of 2. For example:
• The first place is 2⁰ = 1
• The next is 2¹ = 2
• Then 2² = 4 and so on.
So, we can represent numbers like this:
► The number 1 is written as urapon
► The number 2 is written as urapon ukasar
► The number 3 is urapon urapon
► The number 4 becomes urapon ukasar ukasar
Each position tells us how many of that power of 2 we have and we use ukasar for 0 and urapon for 1.
Comparison: If we compare this to the Gumulgal number system, there’s a big difference. The Gumulgal system doesn’t use place value. Instead, it adds groups of 2s (ukasar) and 1s (urapon) to build numbers. For example, to make 7, they would say something like ukasar-ukasar-ukasar-urapon (2 + 2 + 2 + 1).
So the main difference is the base-2 system with ukasar and urapon is a place value system — more efficient and better for large numbers. The Gumulgal system is group-based and additive, which is fine for small numbers but becomes confusing as numbers get bigger.

3. Where in your daily lives and in which professions, do the Hindu numerals and 0, play an important role? How might our lives have been different if our number system and 0 hadn’t been invented or conceived of?
See SolutionHindu numerals and the digit 0 are used every day in our lives—for telling time, counting money, reading prices, doing math in school and writing phone numbers. Many professions like banking, teaching, engineering and science rely heavily on this number system. Zero plays a key role in place value and calculations, making big numbers easy to write and understand.
If zero and the Hindu number system had not been invented, life would be very difficult. We would struggle to calculate, trade or even write dates properly. Modern technology like computers and calculators would not exist, slowing down progress in every field.

4. The ancient Indians likely used base 10 for the Hindu number system because humans have 10 fingers and so we can use our fingers to count. But what if we had only 8 fingers? How would we be writing numbers then? What would the Hindu numerals look like if we were using base 8 instead? Base 5? Try writing the base-10 Hindu numeral 25 as base-8 and base-5 Hindu numerals, respectively. Can you write it in base-2?
See SolutionIf humans had only 8 fingers:
We would probably have developed a base-8 number system instead of base-10. Just like we now count from 0 to 9 in base-10, we would count from 0 to 7 in base-8. All our numerals, math and calculations would be based on powers of 8.
Conversion of the base-10 number 25:
► In base-8:
25 ÷ 8 = 3 remainder 1
3 ÷ 8 = 0 remainder 3
So, 25 in base-8 = 31
► In base-5:
25 ÷ 5 = 5 remainder 0
5 ÷ 5 = 1 remainder 0
1 ÷ 5 = 0 remainder 1
So, 25 in base-5 = 100
► In base-2 (binary):
25 ÷ 2 = 12 remainder 1
12 ÷ 2 = 6 remainder 0
6 ÷ 2 = 3 remainder 0
3 ÷ 2 = 1 remainder 1
1 ÷ 2 = 0 remainder 1
So, 25 in base-2 = 11001