NCERT Solutions for Class 8 Maths Ganita Prakash Chapter 4 Quadrilaterals

Page 82

Observe the following figures.

See AnswerFigures (i), (ii) and (iii) are quadrilaterals and the others are not. Because these have four angles and four sides.

Page 83

Are there other ways to define a rectangle?
See AnswerYes.
There are other ways to define a rectangle, even though they must mean the same thing.
► Definition (using parallelogram idea): A rectangle is a parallelogram whose all angles are right angles.
► Definition (using one right angle): A parallelogram with even one right angle is a rectangle (because if one angle is 90°, all others automatically become 90°).
► Definition (using diagonals): A quadrilateral whose diagonals are equal and bisect each other is a rectangle.
► Definition (opposite sides equal + right angle): A quadrilateral with opposite sides equal and one right angle is a rectangle.

A carpenter needs to put together two thin strips of wood, as shown in Fig. 1, so that when a thread is passed through their endpoints, it forms a rectangle.

She already has one 8 cm long strip. What should be the length of the other strip? Where should they both be joined?
See AnswerThe length of the other strip should be 8 cm because diagonals of rectangle are equal in length.
The both be joined at the mid-point of the strip that is, at 4 cm from the end point.

1. What is the length of the other diagonal?
See AnswerThe length of other diagonal is 8 cm because diagonals of rectangle are equal in length.

2. What is the point of intersection of the two diagonals?
See AnswerWe know that diagonals of rectangle bisect each other. Therefore, the point of intersection of the two diagonals is mid-point of two diagonals.

3. What should the angle be between the diagonals?
See AnswerOne angle between the diagonals should be acute but the other is obtuse.

Page 85

Can the following equalities be used to establish that ΔAOD ≅ ΔCOB?

AO = CO (proved above)
∠AOB = ∠COD (vertically opposite angles)
AD = CB
See AnswerNo.
As per to establish that ΔAOD ≅ ΔCOB, we need angle between two sides to fulfil the condition of SAS. Here SSA is being applied which is not the rule for coungruency.

Can you find all the remaining angles?

See Answer∠AOB = ∠COD = 60° [Vertically opposite angles]
∠AOB + ∠BOC = 180° [Linear Pair]
⇒ ∠BOC = 180° – ∠AOB
⇒ ∠BOC = 180° – 60° = 120°
∠AOD = ∠COB = 120° [Vertically opposite angles]

Can you find the value of a?

See AnswerIn ΔAOB, OA = OB
Therefore, ∠OAB = ∠OBA = a [The angles opposite them are equal]
So, ∠OAB + ∠OBA + ∠AOB = 180° [Angle sum property of triangle]
⇒ a + a + 60° = 180°
⇒ 2a = 180° – 60° = 120°
⇒ a = 120°/2 = 60°

Page 86

Can we now identify what type of quadrilateral ABCD is?

See AnswerAll angles of the quadrilateral are of 90° and diagonals are not intersecting at right angle, therefore it is a rectangle.

What can we say about its sides?
See AnswerThe opposite sides of rectangle are equal, so it opposite sides should be equal.

Will ABCD remain a rectangle if the angles between the diagonals are changed? Can we generalise this?
Answer:
It will remain rectangle until the angles become right angle. At right angle it would be a square.

Page 87

Can you find the other angles?

See AnswerUsing angle sum property in ΔCOD, ΔAOB, ΔBOC and ΔAOD, we can find each angle.

What is the value of a (in degrees) in terms of x?

See AnswerIn ΔAOB, OA = OB
Therefore, ∠OAB = ∠OBA = a [The angles opposite them are equal]
So, ∠OAB + ∠OBA + ∠AOB = 180° [Angle sum property of triangle]
⇒ a + a + x = 180°
⇒ 2a = 180° – x
⇒ a = (180° – x)/2.

What can we say about AB and CD, and AD and BC?
See AnswerOpposite sides of a rectangle are equal.
Therefore, AB = CD and AD = BC.

Page 89

In the earlier definition, we stated that a rectangle has (a) opposite sides of equal length, and (b) all angles equal to 90°. Would we be wrong if we just define a rectangle as a quadrilateral in which all the angles are 90°?
See AnswerNo, we would not be wrong — but the definition would be incomplete.
If we say: “A rectangle is a quadrilateral in which all angles are 90°”, then it automatically becomes true that the opposite sides are equal.
Because any quadrilateral with all angles 90° must be a parallelogram and in a parallelogram, opposite sides are always equal.
So even if we don’t mention “opposite sides are equal”, the condition all angles = 90° already forces that to happen.

If you think that this definition is incomplete, try constructing a quadrilateral in which the angles are all 90° but the opposite sides are not equal.
Are you able to construct such a quadrilateral?
See AnswerIf I try to draw a quadrilateral with all angles = 90°, this is what happens:
► First, I draw one side AB.
► At A and B, I make right angles and draw the next two sides AD and BC.
► These two sides become parallel to each other.
► Now, to close the figure, I join D and C.
► That last side DC automatically becomes parallel to AB.
So I always end up with both pairs of opposite sides parallel, which means it becomes a parallelogram with all right angles → that is exactly a rectangle.
And in a parallelogram, opposite sides are equal.
So, it is not possible to construct a quadrilateral with all angles 90°, but opposite sides not equal.
Therefore, the definition “a quadrilateral in which all angles are 90°” is actually complete enough for a rectangle.

Consider a quadrilateral ABCD with all angles measuring 90°. What can we say about the opposite sides of such a quadrilateral?
See AnswerIf a quadrilateral ABCD has all angles measuring 90°, then:
► Opposite sides must be parallel:
AB ∥ CD
BC ∥ AD
This happens because when all angles are right angles, the sides automatically become parallel in pairs.
► Opposite sides must also be equal:
Since the opposite sides are parallel and the angles are 90°, the quadrilateral becomes a parallelogram with all right angles — that is, a rectangle.
In every rectangle ABCD, AB = CD and BC = AD
Thus, in a quadrilateral with all angles = 90°, the opposite sides are equal and parallel.

Page 90

Is it wrong to write ΔBAD ≅ ΔCDB? Why?

See AnswerYes, it is wrong to write ΔBAD ≅ ΔCDB in a rectangle ABCD.
In rectangle ABCD, triangles BAD and CDB do not match in size.
In a rectangle, AB = CD and BC = AD (opposite sides are equal).
But triangle BAD uses the sides BA, AD and diagonal BD.
Triangle CDB uses the sides CD, CB and the same diagonal BD.
Even though the diagonal BD is common, the other sides are:
BA vs CD → equal
AD vs CB → equal
But the included angles are different:
In ΔBAD, the angle between BA and AD is ∠BAD.
In ΔCDB, the angle between CD and CB is ∠DCB.
These two angles are not equal.
Therefore, even if two sides are equal, the included angles are not the same.
So the SAS (Side–Angle–Side) condition fails and the triangles cannot be congruent.

Are the opposite sides of a rectangle parallel?
See AnswerYes.
The opposite sides of a rectangle parallel as well as equal in length.

Page 92

Let us consider the Carpenter’s Problem again. If the wooden strips have to be placed such that the thread passing through their endpoints forms a square, what must be done?
See AnswerThe two equal threads should bisect at 90°.

What more needs to be done to get equal sidelengths as well? Can this be achieved by properly choosing the angle between the diagonals?
See AnswerIf the two equal threads bisect at 90°, the sidelenghts automatically become equal.
Yes, it can be achieved by properly choosing 90° angle between the diagonals.

By the SSS condition for congruence, ΔBOA ≅ ΔBOC.
Can this be used to find the angles ∠BOA and ∠BOC formed by the diagonals?

See AnswerIn congrueant triangles, the corresponding parst are equal. So, this can be used to find the angles ∠BOA and ∠BOC formed by the diagonals.

Page 93

Using this fact, construct a square with a diagonal of length 8 cm.
See Answer► Use a ruler to draw a line segment AC of length 8 cm.
► Find the midpoint O of AC.
Take compass more than half of AC.
Draw arcs above and below AC from A.
With the same radius, draw arcs from C.
The arcs intersect at two points.
Join these points to get a perpendicular line.
This perpendicular line meets AC at O, which is the midpoint.
► The line through O perpendicular to AC is the other diagonal BD of the square.
► In a square, diagonals are equal. So BD must also be 8 cm.
With compass at O, radius = half of AC = 4 cm.
Mark two points on the perpendicular bisector:
These are points B and D, each 4 cm from O. So, BO = OD = 4 cm → BD = 8 cm.
► Join A to B, B to C, C to D, and D to A.
This is the required square ABCD.

Verify if this is true by going through geometric reasoning in Deduction
1 and Deduction 2, and see if they apply to a square as well.
See AnswerIn a square, both deductions are fully true based on geometric reasoning. First, the diagonals of a square are always equal in length. This is because a square is a special parallelogram in which all angles are 90° and all sides are equal. Since the diagonals meet at right angles and split the square into four congruent right triangles, each half of both diagonals is equal. This makes the full lengths of AC and BD equal, so if one diagonal is 8 cm, the other must also be 8 cm. Second, the diagonals of a square always bisect each other. A square has opposite sides parallel, so it behaves like a parallelogram and in every parallelogram, diagonals cut each other into two equal parts. Therefore, the intersection point of the diagonals is the midpoint of both AC and BD. Thus, both Deduction 1 and Deduction 2 hold true for every square.

What are the measures of ∠1, ∠2, ∠3, and ∠4? See if you can reason and/or experiment to figure this out!

See AnswerIn ΔADC, we have,
AD = DC, therefore ∠1 = ∠3.
Using angle sum property in ΔADC:
∠1 + ∠3 + 90° = 180°
⇒ ∠1 + ∠1 + 90° = 180° [Since ∠1 = ∠3]
⇒ 2∠1 + 90° = 180°
⇒ 2∠1 = 90°
⇒ ∠1 = 90°/2 = 45°
Thus, ∠1 = ∠3 = 45°.[Since ∠1 = ∠3]
Similarly, In ΔABC, we have,
AB = BC, therefore ∠4 = ∠2.
Using angle sum property in ΔABC:
∠2 + ∠4 + 90° = 180°
⇒ ∠2 + ∠2 + 90° = 180° [Since ∠2 = ∠4]
⇒ 2∠2 + 90° = 180°
⇒ 2∠2 = 90°
⇒ ∠2 = 90°/2 = 45°
Thus, ∠2 = ∠4 = 45°.[Since ∠2 = ∠4]

Page 94

1. Find all the other angles inside the following rectangles.

See Explanation(i) In ΔOAB
AO = BO [Diagonals of rectangle bisect each other]
∠OBA = ∠OAB = 30° [Angles opposite to equal sides are equal]
Similarly, ∠OCD = ∠ODC = 30°
Now, in ΔOAB
∠OBA + ∠OAB + ∠AOB = 180° [Angle sum property of triangle]
⇒ 30° + 30° + ∠AOB = 180°
⇒ ∠AOB = 180° – 60°
⇒ ∠AOB = 120°
∠AOB = ∠DOC = 120° [Vertically opposite angles]
∠BOC + ∠AOB = 180° [Linear Pair]
⇒ ∠BOC + 120° = 180°
⇒ ∠BOC = 180° – 120° = 60°
∠BOC = ∠AOD = 60° [Vertically opposite angles]
In ΔOBC
BO = CO [Diagonals of rectangle bisect each other]
∠OBC = ∠OCB [Angles opposite to equal sides are equal]
∠OBC + ∠OCB + ∠COB = 180° [Angle sum property of triangle]
⇒ ∠OBC + ∠OBC + 60° = 180° [∠OBC = ∠OCB]
⇒ 2∠OBC = 180° – 60°
⇒ ∠OBC = 120°/2 = 60°
So, ∠OBC = ∠OCB = 60°
Similarly, ∠OAD = ∠ODA = 60°.

2. Draw a quadrilateral whose diagonals have equal lengths of 8 cm that bisect each other, and intersect at an angle of
(i) 30° (ii) 40° (iii) 90° (iv) 140°
Answer:

3. Consider a circle with centre O. Line segments PL and AM are two perpendicular diameters of the circle. What is the figure APML? Reason and/or experiment to figure this out.
See ExplanationFigure APML is a square.
PL and AM are diameters of the circle and are perpendicular to each other. So they cut the circle into four equal parts (four 90° arcs).
The points A, P, M, L lie on the circle at the ends of these diameters. So the arcs AP, PM, ML, LA are all equal.
In a circle, equal arcs have equal chords, so AP = PM = ML = LA
So, all four sides of quadrilateral APML are equal.
Now look at angle at P, ∠APM. It is an angle in a semicircle (made by diameter AM) and we know that angle in a semicircle is 90°.
So ∠APM = 90°.
Similarly, all other angles (at A, M, L) are also 90° because each is formed using a diameter.

4. We have seen how to get 90° using paper folding. Now, suppose we do not have any paper but two sticks of equal length, and a thread. How do we make an exact 90° using these?
See AnswerYou can make an exact 90° angle using two sticks of equal length and a thread by using the idea of a right-angled triangle.
► Take the thread and tie it so that its length is exactly the same as the diagonal of the square you want to form.
► Fix the two sticks so that they meet at one end (like two sides of a square).
► Now stretch the thread between the free ends of the two sticks.
► Adjust the sticks until the stretched thread becomes tight and forms the longest side between the ends.
If the two sticks represent two equal sides and the thread represents the diagonal, then in a square, the diagonal opposite a right angle is the longest side.
When the thread becomes tight, it forces the angle between the sticks to become exactly 90°, because only a right angle fits the diagonal length correctly.

5. We saw that one of the properties of a rectangle is that its opposite sides are parallel. Can this be chosen as a definition of a rectangle? In other words, is every quadrilateral that has opposite sides parallel and equal, a rectangle?
See AnswerNo, this cannot be used as a definition of a rectangle.
If a quadrilateral has opposite sides parallel and equal, it becomes a parallelogram.
But not every parallelogram is a rectangle.
A rectangle needs one more special condition: All angles must be 90°.
In many parallelograms:
► opposite sides are equal
► opposite sides are parallel
► but angles are not 90° (they are slanted)
So a parallelogram may look like a tilted shape, not a rectangle.

Page 94

Is it possible to construct a quadrilateral with three angles equal to 90° and the fourth angle not equal to 90°? But why not?
See AnswerNo, it is not possible to construct a quadrilateral with three angles equal to 90° and the fourth angle not equal to 90°.
The sum of all angles in any quadrilateral is 360°.
If three angles are 90°, then 90° + 90° + 90° = 270°
The fourth angle must be 360° − 270° = 90°
So the fourth angle is forced to be 90°.

Page 95

Are there quadrilaterals that have parallel opposite sides that are not rectangles?
Answer:
Yes, there are quadrilaterals with parallel opposite sides that are not rectangles.
Any quadrilateral whose opposite sides are parallel is called a parallelogram.
But not every parallelogram is a rectangle.
Examples of such quadrilaterals:
► Parallelogram
• Opposite sides are parallel.
• Opposite sides are equal.
• Angles are not necessarily 90°.
► Rhombus
• All sides are equal.
• Opposite sides are parallel.
• Angles are not all 90° (only in a square they are).
► Square is a special case of a parallelogram, but you asked for shapes that are not rectangles, so rhombus and general parallelograms qualify.

Construct such a figure by recalling how parallel lines can be constructed using a ruler and a set-square or a compass and a ruler.
Answer:
Construction of a Parallelogram (Not a Rectangle) (using ruler and set-square OR compass)
Step 1: Draw a line segment AB.
Step 2: Construct a line parallel to AB through a point C.
• Choose a point C anywhere above AB (not vertically above).
• Using a set-square, slide it along the ruler to draw a line through C parallel to AB.
• Mark a point D on this new line.
Now CD ∥ AB.
Step 3: Construct a line through B parallel to CD.
• Again use the set-square to draw a line through B parallel to CD.
• This line will meet the line through C at point D automatically.
So BC ∥ AD.
Step 4: Join A to D and B to C to get quadrilateral ABCD where AB ∥ CD and BC ∥ AD but angles are not 90°
This is a parallelogram, not a rectangle.

Page 96

Is a rectangle a parallelogram?
See AnswerYes, a rectangle is a parallelogram.
A parallelogram is a quadrilateral in which opposite sides are parallel.
In a rectangle:
• Opposite sides are parallel
• Opposite sides are equal
• All angles are 90°
So a rectangle satisfies all the conditions of a parallelogram and has an extra special property (right angles).

Draw a parallelogram with adjacent sides of lengths 4 cm and 5 cm and an angle of 30° between them.
See AnswerStep 1: Draw line segments AB = 4 cm and AD = 5 cm with an angle of 30° between them.
Step 2: Draw a line parallel to AB through the point D and a line parallel to AD through B. Mark the point at which these lines intersect as C.
ABCD is the required parallelogram.

What are the remaining angles of the parallelogram? What are the lengths of the remaining sides? See if you can reason out and/or experiment to figure these out.

See AnswerIn ABCD, ∠A + ∠B = 180° [Adjacent angles of parallelogram]
⇒ 30° + ∠B = 180°
⇒ ∠B = 180° – 30° = 150°
We know that the opposite angles of parallelogram are equal.
∠B = ∠D = 150° and
∠A = ∠C = 30°
Given that AD = 5 cm and AB = 4 cm.
BC = AD = 5 cm [Opposite sides of parallelogram are equal]
DC = AB = 4 cm [Opposite sides of parallelogram are equal]

Page 97

What can we say about the angles of a parallelogram?
See AnswerIn a parallelogram, the adjacent pairs of angles add up to 180° and opposite pairs of angles are equal.

What about the opposite angles? Will they be equal in all parallelograms? If yes, how can we be sure?

See AnswerYes, the opposite angles of a parallelogram are always equal.
We can prove it in the following manner:
Let ∠P = x
Since ∠P + ∠R = 180° [Adjacent angles of parallelogram]
⇒ ∠R = 180° – ∠P = 180° – x.
Similarly, since ∠A + ∠R = 180°,
∠A = 180° – ∠R = 180° – (180 – x) = 180° – 180° + x = x.
Thus, ∠P = ∠A = x.
Similarly, we can deduce that ∠ R = ∠E = 180° – x.
Therefore, it proves that the opposite angles of a parallelogram are always equal.

What can we say about the sides of a parallelogram?
See AnswerThe opposite sides of a parallelogram are equal.

Page 98

Is it wrong to write ΔABD ≅ ΔCBD? Why?

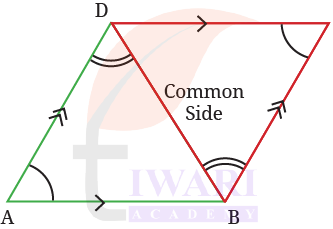
See AnswerYes, it is wrong to write ΔABD ≅ ΔCBD according to the figure.
In the figure:
► The two triangles ABD and CBD share the common side BD.
► They also have some equal angles shown in the figure.
► But for congruence, we need one of these conditions:
• SSS (all three sides equal)
• SAS (two sides and the included angle equal)
• ASA or AAS
• RHS (for right triangles)
In the picture:
1. Only one side (BD) is common.
There is no information showing that AB = BC or AD = CD
So the three-side equality (SSS) is missing.
2. The equal angle markings are not the included angle between known equal sides.
Even if some angles look equal:
• We do not know that the sides around those angles are equal.
• So SAS congruence does not apply.
3. The shape looks like a parallelogram or general quadrilateral.
In such shapes the diagonals (BD) divide the quadrilateral into two triangles,
but these triangles are usually not congruent because the sides differ.

Are the diagonals of a parallelogram always equal? Check with the parallelogram that you have constructed.
See AnswerNo, the diagonals of a parallelogram are not always equal.
In any parallelogram:
► Opposite sides are parallel
► Opposite sides are equal
► Diagonals bisect each other
► But they do not have to be equal in length.
In the parallelogram, that I have constructed, one diagonal is 8 cm where as the other is 4.6 cm.

Do they bisect each other (do they intersect at their midpoints)? Reason and/or experiment to figure this out.
See AnswerYes. The diagonals of a parallelogram always bisect each other.
In a parallelogram:
► Opposite sides are parallel.
► When the diagonals cross, they form pairs of alternate interior angles that are equal.
Because of these equal angles and parallel sides, the triangles formed by the diagonals are congruent, which shows AO = OC and BO = OD
So the diagonals meet at point O, which is the midpoint of both diagonals.

Page 99

Is it wrong to write ΔAOE ≅ ΔSOY? Why?

See AnswerYes, it is wrong to write ΔAOE ≅ ΔSOY.
To prove two triangles congruent, we need one of these rules:
► SSS (all three sides equal)
► SAS (two sides and included angle equal)
► ASA (two angles and included side equal)
► RHS (right angle, hypotenuse, side)
In the figure:
► Triangle AOE is on the left.
► Triangle SOY is on the right.
Even though the diagram shows some equal sides and angles, the positions of angles and sides do not match in the same order, so the triangles cannot be paired correctly under any congruency rule.

Do the diagonals of a parallelogram intersect at a particular angle?
See AnswerNo, the diagonals of a parallelogram do not intersect at any fixed or particular angle.
In a parallelogram:
► The diagonals always bisect each other (they cut each other into two equal halves).
► But the angle at which they intersect can vary.
This angle depends on the shape of the parallelogram:
► Square → diagonals intersect at 90°
► Rectangle → diagonals intersect at not 90° (usually acute/obtuse)
► Rhombus → diagonals intersect at 90°
► General parallelogram → diagonals may intersect at any acute or obtuse angle.

Are squares the only quadrilaterals that have equal sidelengths?
See AnswerNo, squares are not the only quadrilaterals that have all sides equal.
A square has all four sides equal and all angles equal (90°).
But there is another quadrilateral that also has all sides equal:
► Rhombus: A rhombus has:
All four sides equal
Opposite sides are parallel
So, a rhombus is a quadrilateral with all sides equal, but it is not a square unless its angles become 90°.

Can we complete this quadrilateral so that all its sides are of the same length?

See AnswerMeasure AB using a compass, mark a point C whose distance from B and D is equal to AB (or AD). Keeping this length as the radius, cut arcs from B and D.
Now we have a quadrilateral with equal sidelengths and one of its angles 50°.

Page 100

What are the other angles of the rhombus ABCD that we have constructed?
See Answer∠A + ∠B = 180° [Adjacent angles]
⇒ 50° + ∠B = 180° [∠A = 50°]
⇒ ∠B = 180° – 50° = 130°
Now,
∠A = ∠C = 50° [Opposite angles of parallelogram]
∠B = ∠D = 130° [Opposite angles of parallelogram]

It can be seen that ΔGAE ≅ ΔMAE (How?)

See AnswerIn ΔGAE and ΔMAE
GE = ME [Sides of rhombus]
GA = MA [Sides of rhombus]
AE = EA [Common]
So, by SSS rule, ΔGAE ≅ ΔMAE.

Page 101

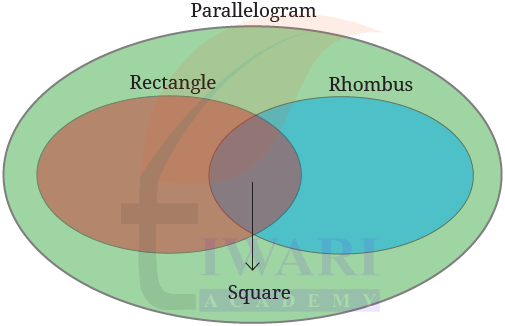
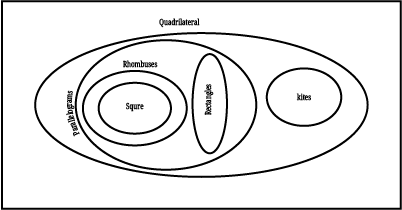
So a rhombus is a parallelogram and a rectangle is also a parallelogram. How can this be represented using a Venn diagram?
Where will the set of squares occur in this diagram?
Answer:

Are the diagonals of a rhombus equal?
See AnswerNo, the diagonals of a rhombus are not equal.

Page 102

Do the diagonals of a rhombus intersect at any particular angle?
See AnswerYes, the diagonals of a rhombus always intersect at a particular angle: they meet at a right angle (90°).
In a rhombus:
► The diagonals are not equal, but
► They always cut each other exactly in half (bisect each other) and
► They always intersect at 90°, forming four right angles at their intersection point.
This property is true for every rhombus.

In the rhombus GAME, we have ΔGEO ≅ ΔMEO. why?

See AnswerIn ΔGEO and ΔMEO
EG = EM [Sides of rhombus]
GO = MO [Digonals of rhombus bisect each other]
EO = EO [Common]
So, by SSS rule ΔGEO ≅ ΔMEO.

Page 102

1. Find the remaining angles in the following quadrilaterals.

See Explanation(i) ∠P + ∠E = 180° [Adjacent angles]
⇒ 40° + ∠E = 180° [∠P = 40°]
⇒ ∠E = 180° – 40° = 140°
∠R = ∠E = 140° [Opposite angles of parallelogram]
∠A = ∠P = 40° [Opposite angles of parallelogram]
(ii) ∠P + ∠Q = 180° [Adjacent angles]
⇒ 110° + ∠Q = 180° [∠P = 110°]
⇒ ∠Q = 180° – 110° = 70°
∠S = ∠Q = 70° [Opposite angles of parallelogram]
∠R = ∠P = 110° [Opposite angles of parallelogram]
(iii) In ΔXUV
UX = UV [Sides of rhombus]
So, ∠UXV = ∠UVX = 30° [Angles opposite to equal sides]
Now, ∠UXV + ∠UVX + ∠U = 180° [Angle sum property of triangle]
⇒ 30° + 30°+ ∠U = 180°
⇒ ∠U = 180° – 60° = 120°
∠W = ∠U = 120° [Opposite angles of rhombus]
In ΔXWV
WX = WV [Sides of rhombus]
So, ∠WXV = ∠WVX [Angles opposite to equal sides]
Now, ∠WXV + ∠WVX + ∠W = 180° [Angle sum property of triangle]
⇒ ∠WXV + ∠WXV + 120° = 180° [∠WXV = ∠WVX]
⇒ 2∠WXV + 120° = 180°
⇒ 2∠WXV = 180° – 120° = 60°
⇒ ∠WXV = 60°/2 = 30°
(iv) In ΔEAO
AE = AO [Sides of rhombus]
So, ∠AOE = ∠AEO = 20° [Angles opposite to equal sides]
Now, ∠AOE + ∠AEO + ∠A = 180° [Angle sum property of triangle]
⇒ 20° + 20°+ ∠A = 180°
⇒ ∠A = 180° – 40° = 140°
∠I = ∠A = 140° [Opposite angles of rhombus]
In ΔOIE
OI = IE [Sides of rhombus]
So, ∠IEO = ∠IOE [Angles opposite to equal sides]
Now, ∠IEO + ∠IOE + ∠I = 180° [Angle sum property of triangle]
⇒ ∠IEO + ∠IEO + 140° = 180° [∠IEO = ∠IOE]
⇒ 2∠IEO + 140° = 180°
⇒ 2∠IEO = 180° – 140° = 40°
⇒ ∠IEO = 40°/2 = 20°

2. Using the diagonal properties, construct a parallelogram whose diagonals are of lengths 7 cm and 5 cm, and intersect at an angle of 140°.
Steps of ConstructionSteps of Construction:
► Draw a straight line segment AC = 7 cm.
► To find the midpoint of AC, mark the midpoint O of AC by measuring 3.5 cm from A or C.
► At point O, use a protractor to construct an angle of 140°.
► Draw a line through O along this angle. This will be the direction of the second diagonal.
► Mark half of the shorter diagonal (2.5 cm) on both sides of O. Since the diagonals of a parallelogram bisect each other, the half-length of the shorter diagonal = 5 ÷ 2 = 2.5 cm.
► From O, measure 2.5 cm on each side along the 140° line. Mark these points as B and D.
► Join the vertices, to get ABCD, the required parallelogram.

3. Using the diagonal properties, construct a rhombus whose diagonals are of lengths 4 cm and 5 cm.
Steps of ConstructionSteps of Construction:
► Draw a point O. This will be the point where the diagonals intersect.
► Draw a line through O and mark 2.5 cm on both sides of O.
► Mark point A 2.5 cm to the left of O. Mark point C 2.5 cm to the right of O. Thus, AC = 5 cm (full diagonal).
► Construct a perpendicular line to AC at point O. Use a set-square or compass to draw a line at 90° to AC.
► On the perpendicular line, mark 2 cm on both sides of O. Mark point B 2 cm above O.
► Mark point D 2 cm below O. Thus, BD = 4 cm (full diagonal).
► Join the points A–B, B–C, C–D, and D–A.
The figure formed is the required rhombus ABCD.

Page 103

Join the ends.
What is the quadrilateral that you get? Justify your answer.

See AnswerWe will get a square because the diagonals are equal and bisecting each other at right angle.

Extend one of the diagonals on both sides by 2 cm.
What quadrilateral will you get now? Justify your answer.
See AnswerWe will get a rhombus because the diagonals are unequal and bisecting each other at right angle.

Page 104

Can you join them to get a quadrilateral?
What type of a quadrilateral is this? Justify your answer.

See AnswerYes we can join them taking one side as common to get a quadrilateral. Since all sides of quadrilateral are equal and its diagonals are not equal so it is a rhombus.

Take two cardboard cutouts of an isosceles triangle with sidelengths 8 cm, 8 cm and 6 cm.
What are the different ways they can be joined to get a quadrilateral?
What quadrilaterals are these? Justify your answers.

Explanation:
We can join them taking one 6 cm side as common to get a quadrilateral. In this condition all sides of quadrilateral are equal and its diagonals are not equal so it is a rhombus.
We can join them taking one 8 cm side as common to get a quadrilateral. In this condition opposite sides of quadrilateral are equal so it is a parallelogram.

Page 105

Take two cardboard cutouts of a scalene triangle with sides 6 cm, 9 cm and 12 cm.
What are the different ways they can be joined to get a quadrilateral?
Are you able to identify the different quadrilaterals that are obtained by joining the triangles? Justify your answer whenever you identify a quadrilateral.

Explanation:
We can join them taking one 12 cm side as common to get a quadrilateral. In this condition its two pair of adjacent sides of quadrilateral are equal so it is a kite.

We can join them taking one 6 cm side as common to get a quadrilateral. In this condition opposite sides of quadrilateral are equal so it is a parallelogram.

We can join them taking one 9 cm side as common to get a quadrilateral. In this condition opposite sides of quadrilateral are equal so it is a parallelogram.

Property 1: In the kite, show that the diagonal BD
(i) bisects ∠ABC and ∠ADC,
(ii) bisects the diagonal AC, that is, AO = OC, and is perpendicular to it.

See AnswerLet the diagonals of kite ABCD intersect at O.
Given: AB = BC and AD=DC (pairs of equal sides of the kite).
(i) To prove BD bisects ∠ABC and ∠ADC
Consider △ABD and △CBD:
AB = CB (sides of the kite)
AD = CD (sides of the kite)
BD = BD (common side)
So, △ABD ≅△ CBD by SSS.
Hence, by CPCTC: ∠ABD = ∠DBC and ∠ADB = ∠CDB
So, BD bisects ∠ABC and ∠ADC.
(ii) To prove BD bisects AC (i.e. AO = OC) and is ⟂ to AC
Now consider △AOB and △COB:
AB = CB (given, sides of kite)
∠ABO = ∠CBO (since BD bisects ∠ABC, from part (i))
OB = OB (common side)
So, △AOB ≅ △COB by SAS.
Therefore, by CPCTC: AO = OC
So BD bisects AC.
Also, ∠AOB = ∠COB.
But ∠AOB + ∠COB = 180 (they form a straight line along AC).
Since they are equal and add to 180, each is 90. So BD ⊥ AC.

Page 106

Construct a trapezium. Measure the base angles (marked in the figure).
Can you find the remaining angles without measuring them?

See AnswerBy measurment: ∠S = 75° and ∠R = 65°
Since PQ||SR, we have
∠S + ∠P = 180°
⇒ 75° + ∠P = 180°
⇒ ∠P = 180° – 75° = 105°
and ∠R + ∠Q = 180°
⇒ ∠R + 65° = 180°
⇒ ∠R = 180° – 65° = 115°

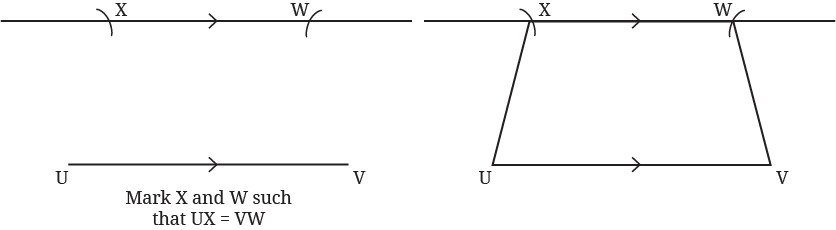
How do we construct an isosceles trapezium?
Construct an isosceles trapezium UVWX, with UV||XW. Measure ∠U.
See AnswerSteps to Construct an Isosceles Trapezium UVWX (with UV ∥ XW)
• Draw a straight line segment UV of any convenient length.
• Draw a parallel line to UV.
• At point U, draw an arc which intersect the parallel line at X.
• At point V, with the same distance, draw an arc which intersect parallel line at W.
• Join X to U and and W to V.
Using a protractor we get ∠U = 80°.
Quadrilateral UVWX is now an isosceles trapezium because UV ∥ XW and UX = VW.

What type of quadrilateral is XWZY?

See AnswerSince XW||UV,
a = 180° – ∠XYZ = 90° and
b = 180° – ∠WZY = 90° (since the internal angles on the same side of a transversal
add up to 180°)
Hence, XWZY is a rectangle.

Page 107

Now, it can be shown that ΔUXY ≅ ΔVWZ. (How?)

See AnswerIn ΔUXY and ΔVWZ
∠XYU = ∠WZV [Each 90°]
UX = VW [Sides of isosceles trapezium]
XY = WZ [Opposite sides of rectangle]
Therefore, by RHS rule
ΔUXY ≅ ΔVWZ

Page 107

1. Find all the sides and the angles of the quadrilateral obtained by joining two equilateral triangles with sides 4 cm.
See AnswerThe lengths of all sides are 4 cm and angles are of 60°, 120°, 60° and 120°.

2. Construct a kite whose diagonals are of lengths 6 cm and 8 cm.
Answer:

3. Find the remaining angles in the following trapeziums —

Answer:

See Explanation∠A + ∠D = 180° [Adjacent angles]
⇒ ∠A + 135° = 180° [Since ∠D = 135°]
⇒ ∠A = 180° – 135° = 45°
Similarly ∠B + ∠C = 180°
⇒ ∠B + 105° = 180° [Since ∠C = 105°]
⇒ ∠B = 180° – 105° = 75°
∠S + ∠P = 180° [Adjacent angles]
⇒ ∠S + 100° = 180° [Since ∠P = 100°]
⇒ ∠S = 180° – 100° = 80°
∠P = ∠Q = 100° [Adjacent angles of issoceles trapezium]
∠R + ∠Q = 180° [Adjacent angles]
⇒ ∠R + 100° = 180° [Since ∠Q = 100°]
⇒ ∠R = 180° – 100° = 80°

4. Draw a Venn diagram showing the set of parallelograms, kites, rhombuses, rectangles, and squares. Then, answer the following questions —
(i) What is the quadrilateral that is both a kite and a parallelogram?
(ii) Can there be a quadrilateral that is both a kite and a rectangle?
(iii) Is every kite a rhombus? If not, what is the correct relationship between these two types of quadrilaterals?
See Answer(i) A rhombus is the quadrilateral that is both:
► a kite (because it has two pairs of equal adjacent sides) and
► a parallelogram (because opposite sides are parallel).
So, rhombus = kite + parallelogram.
(ii) Yes, but only in one special case.
A square is the quadrilateral that is both:
► a kite (all sides equal → two pairs of adjacent equal sides) and
► a rectangle (all angles 90°).
So, a square is both a kite and a rectangle.
(iii) No, every kite is NOT a rhombus.
Correct relationship:
► Every rhombus is a kite (because it has two pairs of equal adjacent sides).
► But every kite is not a rhombus, because in a rhombus all four sides are equal, but in a kite only two pairs of adjacent sides are equal.

5. If PAIR and RODS are two rectangles, find ∠IOD.

See AnswerIn ΔRIO
∠ORI + ∠IOR + ∠I = 180° [Angles sum property of triangle]
⇒ ∠ORI + ∠IOR + 90° = 180° [Since ∠I = 90°, angle of rectangle PAIR]
⇒ 30° + ∠IOR + 90° = 180° [Since ∠ORI = 30°]
⇒ ∠IOR + 120° = 180°
⇒ ∠IOR = 180° – 120° = 60°
Now, ∠IOD + ∠IOR = 90° [Since ∠DOR = 90°, angle of rectangle RODS]
⇒ ∠IOD + 60° = 90° [Since ∠IOR = 60°]
⇒ ∠IOD = 90° – 60° = 30°

6. Construct a square with diagonal 6 cm without using a protractor.
Answer:

7. CASE is a square. The points U, V, W and X are the midpoints of the sides of the square. What type of quadrilateral is UVWX? Find this by using geometric reasoning, as well as by construction and measurement. Find other ways of constructing a square within a square such that the vertices of the inner square lie on the sides of the outer square, as shown in Figure (b).

See AnswerUVWX is a square.
Geometric Reasoning:
Let CASE be a square.
Points U, V, W, X are midpoints of CA, AS, SE, EC respectively.
(a) UVWX is a parallelogram
Using the midpoint theorem:
In △CAS, U and V are midpoints ⇒ UV ∥ CS
In △ASE, V and W are midpoints ⇒ VW ∥ AE
In △SEC, W and X are midpoints ⇒ WX ∥ CS
In △CEA, X and U are midpoints ⇒ XU ∥ AE
Hence, UVWX is a parallelogram.
UV ∥ CS and VW ∥ AE.
In a square, diagonals CS ⟂ AE. A parallelogram with all sides equal and one right angle is a square.
The other ways of constructing a square within a square such that the vertices of the inner square lie on the sides of the outer square are given below:

8. If a quadrilateral has four equal sides and one angle of 90°, will it be a square? Find the answer using geometric reasoning as well as by construction and measurement.
See ExplanationGeometric Reasoning: Let the quadrilateral be ABCD with the following properties:
AB = BC = CD = DA (all four sides equal)
∠D = 90°
A quadrilateral with all four sides equal is a rhombus.
In any rhombus, opposite sides are parallel because it is also a parallelogram.
In a parallelogram, if one angle is 90°, then all four angles become 90° (opposite and adjacent angles adjust automatically).
Therefore, a rhombus with even one right angle becomes a rectangle.
So we get a figure that is: a rhombus (all sides equal) and a rectangle (all angles 90°).
A quadrilateral that is both a rhombus and a rectangle is a square.

9. What type of a quadrilateral is one in which the opposite sides are equal? Justify your answer.
See AnswerA quadrilateral in which the opposite sides are equal is a parallelogram.
Justification:
If in a quadrilateral ABCD:
► AB = CD (one pair of opposite sides equal), and
► BC = AD (other pair of opposite sides equal),
then this matches a known property of parallelograms:
In a parallelogram, opposite sides are equal and parallel. Also, the converse is true:
If both pairs of opposite sides in a quadrilateral are equal, then the quadrilateral must be a parallelogram.
• The equal sides ensure that the triangles formed by drawing one diagonal become congruent (by SSS).
• From congruency, alternate interior angles become equal.
• Equal alternate interior angles imply the opposite sides are parallel.
• A quadrilateral with both pairs of opposite sides parallel is a parallelogram.

10. Will the sum of the angles in a quadrilateral such as the following one also be 360°? Find the answer using geometric reasoning as well as by constructing this figure and measuring.

See AnswerThe sum of the angles in a quadrilateral such as the following one also will be 360°.
After measurement, we get:
∠A = 40°
∠B = 50°
∠C = 40°
∠D = 230°

11. State whether the following statements are true or false. Justify your answers.
(i) A quadrilateral whose diagonals are equal and bisect each other must be a square.
See Answer(i) False.
If a quadrilateral has diagonals that are equal and bisect each other, it is a rectangle. A square is a special rectangle with all sides equal. Here, nothing is said about all four sides being equal, so it need not be a square.

(ii) A quadrilateral having three right angles must be a rectangle.
See Answer(ii) True.
Sum of angles of a quadrilateral = 360°.
If three angles are 90° each, then
90° + 90° + 90° = 270°
Fourth angle = 360° − 270° = 90°.
So all four angles are right angles → it is a rectangle (or possibly a square, which is also a rectangle).

(iii) A quadrilateral whose diagonals bisect each other must be a parallelogram.
See Answer(iii) True.
If the diagonals bisect each other, each diagonal is cut into two equal parts. This is the converse property of a parallelogram. So any quadrilateral whose diagonals bisect each other must be a parallelogram.

(iv) A quadrilateral whose diagonals are perpendicular to each other must be a rhombus.
See Answer(iv) False.
If diagonals are perpendicular, the quadrilateral could be a kite or even some other shape, not necessarily a rhombus. In a rhombus, diagonals are perpendicular and bisect each other, but perpendicularity alone is not enough to guarantee it is a rhombus.

(v) A quadrilateral in which the opposite angles are equal must be a parallelogram.
See Answer(v) True.
If in a quadrilateral, opposite angles are equal, then the quadrilateral is a parallelogram (converse of a property of parallelograms: in a parallelogram, opposite angles are equal).

(vi) A quadrilateral in which all the angles are equal is a rectangle.
See Answer(vi) True.
If all angles in a quadrilateral are equal, each must be 360° ÷ 4 = 90°.
A quadrilateral with all angles 90° is a rectangle (a square is a special case of a rectangle).

(vii) Isosceles trapeziums are parallelograms.
See Answer(vii) False.
An isosceles trapezium has only one pair of opposite sides parallel and the other pair equal but not parallel. A parallelogram must have both pairs of opposite sides parallel. So, in general, isosceles trapeziums are not parallelograms (only a very special case would become a rectangle, but that would no longer be just a trapezium).