NCERT Solutions for Class 8 Maths Ganita Prakash Chapter 5 Number Play

Page 112

Explore these questions and any others that may occur to you. Discuss them with the class.
See AnswerExploring these questions:
Here it is given some interesting questions about sums of consecutive numbers:
► Can every natural number be written as a sum of consecutive numbers?
► Can some numbers be written in more than one way?
► All odd numbers can be written as a sum of two consecutive numbers — but what about even numbers?
► Can we write 0 as a sum of consecutive numbers (maybe with negative numbers)?
Here is what I would explore and discuss:
► Can every natural number be written as a sum of consecutive numbers?
Not every number behaves the same.
• Many numbers can be written as a sum of consecutive numbers (like 7 = 3+4).
• Some numbers cannot, especially powers of 2 (like 1, 2, 4, 8, 16).
This is fun to test with several examples!
► Which numbers can be written in more than one way?
Some numbers like 15 can be written in many ways:
• 15 = 7 + 8
• 15 = 4 + 5 + 6
• 15 = 1 + 2 + 3 + 4 + 5
So, numbers with more divisors usually have more ways.
► All odd numbers = sum of two consecutive numbers — is this always true?
Yes!
Any odd number like 2n+1 can always be written as n + (n+1).
Example:
• 9 = 4 + 5
• 21 = 10 + 11
► Can we write even numbers as a sum of consecutive numbers?
Some even numbers work, some don’t:
• 10 = 1+2+3+4
• 12 = 3+4+5
But
• 8 cannot be written using positive consecutive numbers.
So I would test many even numbers and look for patterns.
► Can 0 be written as a sum of consecutive numbers?
If we only use positive numbers, no.
But if we allow negative numbers, then yes:
• –1 + 0 + 1 = 0
This part makes the discussion more fun.

Take any 4 consecutive numbers. For example, 3, 4, 5, and 6. Place ‘+’ and ‘–’ signs in between the numbers. How many different possibilities exist? Write all of them.
See AnswerThere are 8 different possibilities exist, which are as follows:
► 3 + 4 + 5 + 6
► 3 + 4 + 5 – 6
► 3 + 4 – 5 + 6
► 3 + 4 – 5 – 6
► 3 – 4 + 5 + 6
► 3 – 4 + 5 – 6
► 3 – 4 – 5 + 6
► 3 – 4 – 5 – 6

Page 113

Evaluate each expression and write the result next to it. Do you notice anything interesting?
See Answer► 3 + 4 + 5 + 6 = 18
► 3 + 4 + 5 – 6 = 6
► 3 + 4 – 5 + 6 = 8
► 3 + 4 – 5 – 6 = -4
► 3 – 4 + 5 + 6 = 10
► 3 – 4 + 5 – 6 = -2
► 3 – 4 – 5 + 6 = 0
► 3 – 4 – 5 – 6 = -12

Now, take four other consecutive numbers. Place the ‘+’ and ‘–’ signs as you have done before. Find out the results of each expression. What do you observe?
See AnswerLet’s take another set of four consecutive numbers: 7, 8, 9, 10
There will again be 8 expressions.
► 7 + 8 + 9 + 10 = 34
► 7 + 8 + 9 – 10 = 14
► 7 + 8 – 9 + 10 = 16
► 7 + 8 – 9 – 10 = -4
► 7 – 8 + 9 + 10 = 18
► 7 – 8 + 9 – 10 = -2
► 7 – 8 – 9 + 10 = 0
► 7 – 8 – 9 – 10 = -20
Observation:
• All results are even numbers.
• Just like the previous example with 3, 4, 5, 6, every expression gives an even result.
• This is exactly that when we take any four consecutive numbers, no matter how we place ‘+’ or ‘–’, the final sum is always even.

Repeat this for one more set of 4 consecutive numbers. Share your findings.
See AnswerThe results of one more set of 4 consecutive numbers:
► 11 + 12 + 13 + 14 = 50
► 11 + 12 + 13 – 14 = 22
► 11 + 12 – 13 + 14 = 24
► 11 + 12 – 13 – 14 = -4
► 11 – 12 + 13 + 14 = 26
► 11 – 12 + 13 – 14 = -2
► 11 – 12 – 13 + 14 = 0
► 11 – 12 – 13 – 14 = -28
Our Findings:
Just like the earlier sets:
✔ All results are even numbers.
✔ Some results repeat (e.g., –4 appears again).
✔ We get a mix of positive, zero and negative even numbers.
This confirms the pattern for any four consecutive numbers, all possible +/– combinations always give even results.

Do these patterns occur no matter which 4 consecutive numbers are chosen? Is there a way to find out through reasoning?
See AnswerYes, these patterns occur for any 4 consecutive numbers.
Reason: Take numbers n, n + 1, n + 2, n + 3.
Add them (ignoring +/– signs): n + (n + 1) + (n + 2) + (n + 3) = 4n + 6 = 2(2n + 3)
This is always even.
Since + and – do not change whether a number is odd or even, every possible expression will also be even.
Therefore, no matter which 4 consecutive numbers we choose, all results will always be even.

Page 114

Is there a way to explain why this happens?
See AnswerYes! Here is the explanation in a simple way:
Four consecutive numbers are always: n, n + 1, n + 2, n + 3
Among these:
n and n + 2 are either both even or both odd
n + 1 and n + 3 are also either both even or both odd
So, they form two pairs of numbers with the same parity.
When you add or subtract numbers in pairs like this:
even ± even = even
odd ± odd = even
So every pair gives an even result.
Then you add two even results: even + even = even
Therefore, no matter how you put the + or – signs, the final answer is always even.

Replace any negative sign in the expression a + b – c – d with a positive sign and find the difference between the two numbers.
See AnswerOriginal expression: a + b – c – d
If we change the sign of c from – to +
New expression: a + b + c – d
Difference = (a + b + c – d) – (a + b – c – d) = 2c.

What do you conclude from this observation?
See AnswerConclusion: When we change a negative sign to a positive sign in the expression a + b – c – d, the value of the whole expression increases by twice the number whose sign we changed.
From the example:
We changed the sign of c:
Old term: –c
New term: +c
Difference: (+c) – (−c) = 2c
So the total expression increases by 2c.

Page 115

Is the phenomenon of all the expressions having the same parity limited to taking 4 numbers? What do you think?
See Answera ± b ± c ± d have the same parity is that changing any one sign only changes the value by an even number. If switching signs always changes the result by an even number, the parity can never change.
This reasoning does not depend on taking exactly 4 numbers. It depends only on this fact:
Changing a sign flips a number from +x to –x or vice-versa and that always changes the total by 2x (an even number).
So the same idea works for any number of terms:
• For 3 numbers: a ± b ± c
• For 5 numbers: a ± b ± c ± d ± e
• For 10 numbers
• For 100 numbers
In every case switching any sign changes the value by an even amount.
So all expressions formed from the same set of numbers must have the same parity.

Using our understanding of how parity behaves under different operations, identify which of the following algebraic expressions give an even number for any integer values for the letter-numbers.

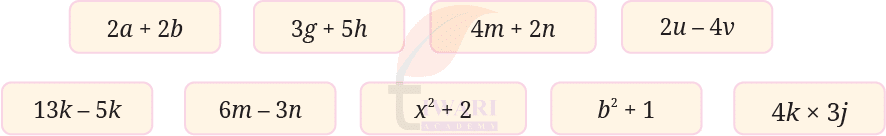
See Answer► 2a + 2b
2a is always even
2b is always even
Sum of two even numbers = even
► 3g + 5h
3g may be odd or even
5h may be odd or even
odd + odd = even
even + even = even
BUT odd + even = odd
So, Not always even
► 4m + 2n
4m is even
2n is even
Sum = even
► 2u – 4v
2u is even
4v is even
Difference of two even numbers = even
► 13k – 5k
Simplifies to (13k – 5k) = 8k
8k is always even
Always even
► 6m – 3n
6m is always even
3n may be odd or even
even – odd = odd
So, Not always even
► x² + 2
x² is even if x is even
x² is odd if x is odd
odd + 2 = odd
So, Not always even
► b² + 1
b² is even if b is even
b² is odd if b is odd
odd + 1 = even
even + 1 = odd
So, Not always even
► 4k × 3j
4k is even
even × anything = even
Always even.

Page 116

Similarly, determine and explain which of the other expressions always give even numbers. Write a couple of examples and non-examples, as appropriate, for each expression.
Write a few algebraic expressions which always give an even number.
See AnswerOther Expressions:
1. 6p + 4q
Both 6p and 4q are even → even + even = even.
Examples
• p = 1, q = 2 → 6 + 8 = 14 (even)
• p = –3, q = 5 → –18 + 20 = 2 (even)
2. 10x – 2y
10x is even, 2y is even → difference is even.
Examples
• x = 3, y = 4 → 30 – 8 = 22 (even)
• x = –2, y = 7 → –20 – 14 = –34 (even)
3. 8a × b
8a is even → even × anything = even.
Examples
• a = 2, b = 5 → 16 × 5 = 80 (even)
• a = –1, b = –3 → –8 × –3 = 24 (even)
4. 2(m² + n²)
m² + n² is an integer → multiplying by 2 makes it even.
Examples
• m = 3, n = 4 → 2(9 + 16) = 2×25 = 50 (even)
• m = –2, n = –1 → 2(4 + 1) = 2×5 = 10 (even)
5. 4(p + q + r)
4 × anything = multiple of 4 → always even.
Examples
• p = 1, q = 1, r = 1 → 4×3 = 12 (even)
• p = –4, q = 2, r = 0 → 4×–2 = –8 (even)
6. 12k – 8m
12k and 8m both are multiples of 4.
Examples
• k = 1, m = 1 → 12 – 8 = 4 (even)
• k = –3, m = 2 → –36 – 16 = –52 (even)
7. 2(a + b + c + d)
2 times any integer is even.
Examples
• a = 2, b = 5, c = –3, d = 1 → sum = 5 → 2×5 = 10 (even)
• a = 0, b = 0, c = 0, d = 7 → 2×7 = 14 (even)
8. (x – y)² – (x + y)²
Expand:
(x – y)² – (x + y)²
= (x² – 2xy + y²) – (x² + 2xy + y²)
= –4xy → always even
Examples
• x = 3, y = 1 → –4×3×1 = –12 (even)
• x = –2, y = 5 → –4×–2×5 = 40 (even)

Take a pair of even numbers. Add them. Is the sum divisible by 4?
See AnswerNo, the sum of two even numbers is not always divisible by 4.
Sometimes it is divisible by 4, sometimes it is not.
This depends on the type of even numbers we choose.
Every even number is either:
1. A multiple of 4 → (numbers like 4, 8, 12, 16…) These leave a remainder 0 when divided by 4.
2. An even number but NOT a multiple of 4 → (numbers like 2, 6, 10, 14…) These leave remainder 2 when divided by 4.
Case 1: Two multiples of 4
Example: 8 and 12
8 + 12 = 20 → 20 is a multiple of 4.
Case 2: Two even numbers NOT multiples of 4
Example: 6 and 10
6 + 10 = 16 → 16 is a multiple of 4
Case 3: One multiple of 4 and one not
Example: 4 and 6
4 + 6 = 10 → 10 is NOT a multiple of 4
So, if one even number is a multiple of 4 and the other is not, their sum is NOT divisible by 4.

Page 117

When will two even numbers add up to give a multiple of 4?
See AnswerTwo even numbers will add up to a multiple of 4 when they are of the same type:
► Both are multiples of 4
Examples: 4, 8, 12, 16, …
Example: 8 + 12 = 20 → 20 is a multiple of 4
► Both are even but NOT multiples of 4
These numbers are of the form 4k + 2 (remainders 2 when divided by 4).
Examples: 2, 6, 10, 14, …
Example: 6 + 10 = 16 → 16 is a multiple of 4.

Look at the following expressions and the visualisation. Write the corresponding explanation and examples.

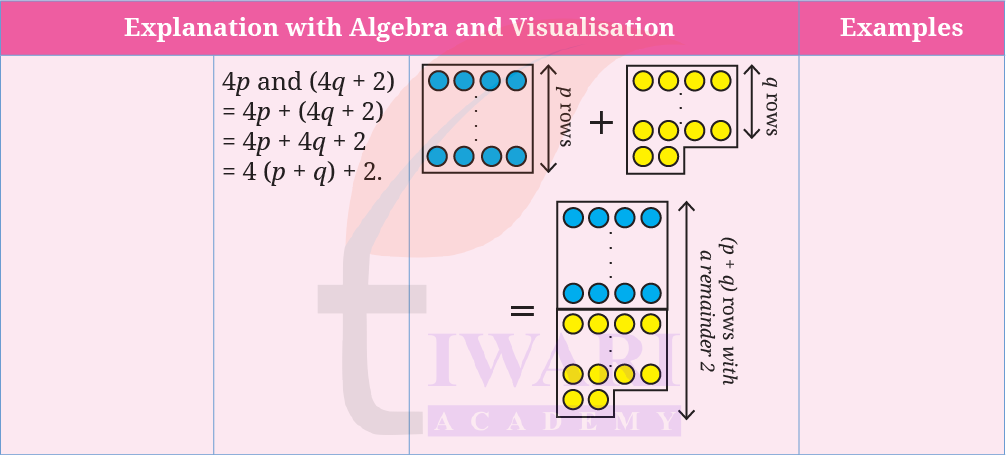
Answer:

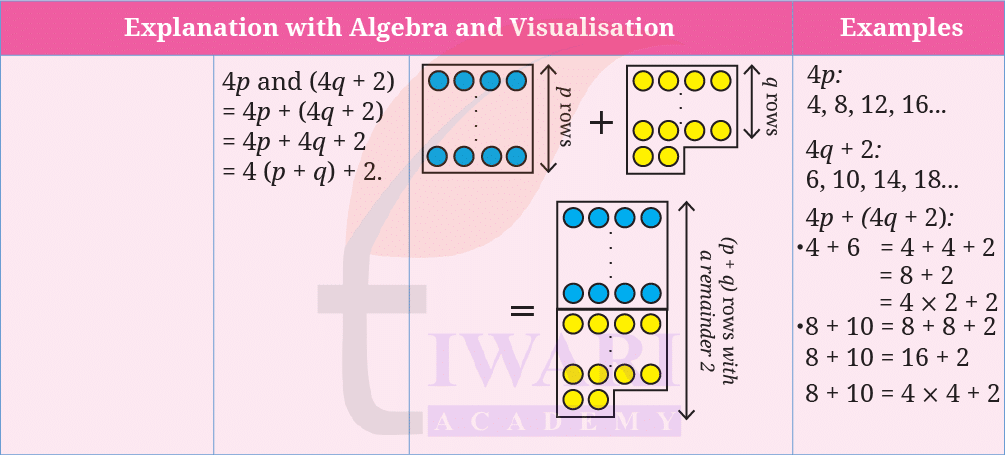
Page 118

We examine different statements about factors and multiples and determine whether a statement is ‘Always True’, ‘Sometimes True’, or ‘Never True’.
See AnswerExamples of Statements and Their Classification
1. “The product of a multiple of 6 and a multiple of 3 is a multiple of 9.”
Example: 6 × 3 = 18 → 18 is a multiple of 9
So, it is always true.
2. “The sum of three consecutive even numbers is divisible by 6.”
Example: 4 + 6 + 8 = 18 → divisible by 6
Always True
3. “8(7b – 3) – 4(11b + 1) is a multiple of 12.”
Simplification: 8(7b – 3) – 4(11b + 1)
= 56b – 24 – 44b – 4
= 12b – 28
= 4(3b – 7)
For it to be divisible by 12, we need (3b – 7) to be a multiple of 3.
This happens only for some b.

1. If 8 exactly divides two numbers separately, it must exactly divide their sum.
See AnswerIf 8 divides both numbers, then each number is a multiple of 8.
So let the numbers be 8a and 8b.
Their sum is 8a + 8b = 8(a + b)
This is clearly a multiple of 8.
Examples:
► 16 and 24
16 + 24 = 40 → divisible by 8
► 8 and 56
8 + 56 = 64 → divisible by 8
► 32 and –8
32 + (-8) = 24 → divisible by 8
So, it is always true.
Hence, if two numbers are each divisible by 8, their sum is always divisible by 8.

Page 119

2. If a number is divisible by 8, then 8 also divides any two numbers (separately) that add up to the number.
See AnswerSuppose the number N is divisible by 8.
So let N = 8k
Now the statement says:
If a + b = 8k, then 8 must divide a and 8 must divide b separately.
Let’s check:
Example to show that it is false:
Let N = 24 (divisible by 8)
Choose numbers that add to 24: a = 10 and b = 14
10 + 14 = 24 but 10 ÷ 8 = not divisible and 14 ÷ 8 = not divisible.
So 8 does not divide them.
Other Example to show that it is false.
Let N = 32 (divisible by 8)
Choose numbers that add to 32: a = 20 and b = 12
20 + 12 = 32 but neither 20 nor 12 is divisible by 8.
Example to show that it is true.
Let a = 16, b = 16
16 + 16 = 32 (divisible by 8)
And both 16 and 16 are divisible by 8.
So, it is true.
Therefore, many pairs adding to a multiple of 8 are not divisible by 8 separately. Only some special pairs (like 16 + 16) satisfy the condition.

3. If a number is divisible by 7, then all multiples of that number will be divisible by 7.
See AnswerIf a number n is divisible by 7, then n = 7k
Now take any multiple of n: m = n × t = (7k) × t = 7(kt)
This shows that m is also a multiple of 7.
There is no way to get a multiple of a number divisible by 7 that is not divisible by 7.
Examples:
• n = 14 (divisible by 7)
Multiples: 14, 28, 42, 56 → all divisible by 7
• n = 21
Multiples: 21, 42, 63, 84 → all divisible by 7
• n = –7
Multiples: –7, –14, –21 → all divisible by 7
So, if a number is divisible by 7, then every multiple of that number is also divisible by 7.

Page 120

4. If a number is divisible by 12, then the number is also divisible by all the factors of 12.
See AnswerFactors of 12: 1, 2, 3, 4, 6, 12
If a number N is divisible by 12, then N = 12k for some integer k.
Since 12k can be divided by 2, 3, 4, 6 and 12 without remainder, the number must be divisible by all factors of 12.
Examples:
• 36 is divisible by 12, 6, 4, 3, 2, 1
• 60 is divisible by 12, 6, 4, 3, 2, 1
• 120 is divisible by 12, 6, 4, 3, 2, 1
So, this statement is always true.

5. If a number is divisible by 7, then it is also divisible by any multiple of 7.
See AnswerLet the number be N = 7k.
Let the “multiple of 7” be M = 7m.
The statement claims: if 7k is divisible by 7, then 7k must also be divisible by 7m.
► Example to show that it is true.
N = 21 (divisible by 7)
M = 14 (multiple of 7)
But 21 is not divisible by 14.
So, it is false.
► Example to show that it is true.
N = 35 (divisible by 7)
M = 21 (multiple of 7)
But 35 is not divisible by 21.
So, it is false.
► Example to show that it is true:
Rare case where it works:
N = 42
M = 14
42 ÷ 14 = 3 (integer)
So, it is true.
Therefore, we can say that the statement is sometimes True (not always).

Page 121

Examine each of the following statements, and determine whether it is ‛Always true’, ‛Sometimes true’, ‛Never true’.
6. If a number is divisible by both 9 and 4, it must be divisible by 36.
See AnswerIf a number N is divisible by 9, then N = 9a.
If N is also divisible by 4, then N = 4b.
For a number to be divisible by 36, it must contain the factors of both:
9 = 3² and 4 = 2²
The least common multiple (LCM) of 9 and 4 is LCM(9, 4) = 36
This means any number divisible by both 9 and 4 must be a multiple of 36.
So, it is always true.

7. If a number is divisible by both 6 and 4, it must be divisible by 24.
See AnswerIf a number is divisible by 6, it has factors 2 × 3.
If a number is divisible by 4, it has factors 2 × 2.
Together, the number must contain 2 × 2 × 3 = 12
So any number divisible by both 6 and 4 must be divisible by 12.
► Example to show that it is false:
Let N = 12
12 ÷ 6 = 2 → divisible
12 ÷ 4 = 3 → divisible
But 12 is not divisible by 24.
So the statement fails.
► Example to show that it is false:
Let N = 36
36 ÷ 6 = 6
36 ÷ 4 = 9
36 is not divisible by 24.
So the statement fails.
► Example to show that it is true:
Let N = 48
48 ÷ 6 = 8
48 ÷ 4 = 12
48 is divisible by 24.
So the statement is ture.
Hence, the statement is sometimes true but not always true.

8. When you add an odd number to an even number we get a multiple of 6.
See AnswerOdd + Even = Odd (always)
So the sum is always an odd number.
But multiples of 6 can be: 6, 12, 18, 24, 30, …
All of these are even numbers except none are odd.
So an odd number cannot be a multiple of 6.
For example: Odd = 5 and Even = 8
Sum = 13 (odd, not a multiple of 6)
Similarly: Odd = 7 and Even = 4
Sum = 11 (not a multiple of 6)
So, the statement is never true.

Find a number that has a remainder of 3 when divided by 5. Write more such numbers.
Which algebraic expression(s) capture all such numbers?
(i) 3k + 5
(ii) 3k – 5
(iii) 3k/5
(iv) 5k + 3
(v) 5k – 2
(vi) 5k – 3
See AnswerA number that leaves a remainder of 3 when divided by 5:
Examples: 3, 8, 13, 18, 23, 28, 33, …
These numbers increase by 5 each time.
So, all numbers of the form 5k + 3 give remainder 3 when divided by 5.
Also, 5k – 2 = 5(k – 1) + 3 gives remainder 3.
Now checking the given expression:
(i) 3k + 5: Does not always give remainder 3.
(ii) 3k – 5: Does not always give remainder 3.
(iii) 3k/5: Not an integer expression; not correct.
(iv) 5k + 3: Always gives remainder 3.
(v) 5k – 2: 5k – 2 = 5(k – 1) + 3 → remainder 3.
(vi) 5k – 3: 5k – 3 = 5(k – 1) + 2 → remainder 2, not 3.
Hence, the correct expressions are 5k + 3 and 5k – 2.

Page 122

Let us consider another expression, 5k – 2, and see the values it takes for different values of k.
k: 1, 2, 3, 4, 5
5k – 2:3, 8, 13, 18, 23
Are there other expressions that generate numbers that are 3 more than a multiple of 5?
See AnswerOther expressions that produce numbers of the form (multiple of 5) + 3
► 5k + 3
Examples:
k = 1 → 8
k = 2 → 13
k = 3 → 18
k = 4 → 23
k = 5 → 28
Each number leaves remainder 3 when divided by 5.
► 5(k + 1) – 2
This simplifies to 5(k + 1) – 2 = 5k + 3
► 5(k – 1) + 3
This simplifies to 5(k – 1) + 3 = 5k – 2

Page 122

1. The sum of four consecutive numbers is 34. What are these numbers?
See AnswerLet the four consecutive numbers be n, n + 1, n + 2, n + 3
Their sum is given as 34:
So, n + (n + 1) + (n + 2) + (n + 3) = 34
⇒ 4n + 6 = 34
⇒ 4n = 28
⇒ n = 7
So the four consecutive numbers are 7, 8, 9, 10

2. Suppose p is the greatest of five consecutive numbers. Describe the other four numbers in terms of p.
See AnswerIt is given that p is the greatest, so the others come just before it.
So the other four numbers in terms of p are:
p − 1
p − 2
p − 3
p − 4

3. For each statement below, determine whether it is always true, sometimes true, or never true. Explain your answer. Mention examples and non-examples as appropriate. Justify your claim using algebra.
(i) The sum of two even numbers is a multiple of 3.
See AnswerSometimes True
Let the even numbers be 2a and 2b
Sum = 2a + 2b = 2(a + b)
The sum is always even, but not always a multiple of 3.
► Example to show the statement is true:
6 + 12 = 18 → multiple of 3
Both are even and the sum is divisible by 3.
► Example to show it is false:
4 + 10 = 14 → not a multiple of 3
So, it is sometimes true, because it depends on whether (a + b) is divisible by 3.

(ii) If a number is not divisible by 18, then it is also not divisible by 9.
See AnswerNever True
A number can fail to be divisible by 18 but still be divisible by 9.
Divisible by 18 requires: divisibility by 2 and by 9
So a number divisible by 9 but not by 18 simply needs to be odd.
So, it is never true because many numbers (27, 45, 63, 81…) are divisible by 9 but not by 18.

(iii) If two numbers are not divisible by 6, then their sum is not divisible by 6.
See AnswerSometimes True, Sometimes False
A number divisible by 6 must be divisible by 2 and 3.
If two numbers are not divisible by 6, they can still add up to a multiple of 6.
► Example to show it is false:
4 (not divisible by 6)
2 (not divisible by 6)
4 + 2 = 6 (divisible by 6)
► Example to show it is true:
(Sum is not divisible by 6)
5 + 7 = 12 → not divisible by 6
So, it is sometimes true, sometimes false.

(iv) The sum of a multiple of 6 and a multiple of 9 is a multiple of 3.
See AnswerAlways True
Let 6a = multiple of 6 → 6a = 3(2a)
9b = multiple of 9 → 9b = 3(3b)
Sum: 6a + 9b = 3(2a + 3b)
The sum is clearly a multiple of 3.
► Example to show it is true:
12 + 18 = 30 → multiple of 3
► Example to show it is true:
6 + 45 = 51 → multiple of 3
So, it is always true.

(v) The sum of a multiple of 6 and a multiple of 3 is a multiple of 9.
See AnswerSometimes True
Let: 6a = multiple of 6
3b = multiple of 3
Sum = 6a + 3b = 3(2a + b)
This is always divisible by 3, but it is divisible by 9 only if:
2a + b is divisible by 3
That happens sometimes.
► Example to show it is true:
6 + 3 = 9 → multiple of 9
► Example to show it is false:
6 + 6 = 12 → not a multiple of 9
So, it is sometimes true, not always.

4. Find a few numbers that leave a remainder of 2 when divided by 3 and a remainder of 2 when divided by 4. Write an algebraic expression to describe all such numbers.
See AnswerLet’s find numbers that satisfy both conditions:
Leave remainder 2 when divided by 3
Leave remainder 2 when divided by 4
Condition 1: Remainder 2 when divided by 3 → numbers of the form: 3k + 2
Condition 2: Remainder 2 when divided by 4 → numbers of the form: 4m + 2
We want numbers that satisfy both, so we need numbers of the form: 3k + 2 = 4m + 2
Subtract 2 from both sides: 3k = 4m
This means 3k must be a multiple of 4 or equivalently 4m must be a multiple of 3.
The smallest positive common multiple of 3 and 4 is 12.
So, 3k = 12t ⇒ k = 4t and
4m = 12t ⇒ m = 3t
Now, the number expression: 3k + 2 = 3(4t) + 2 = 12t + 2
Take t = 0, 1, 2, 3 …
t = 0 gives 2
t = 1 gives 14
t = 2 gives 26
t = 3 gives 38
t = 4 gives 50
t = 5 gives 62
So some numbers are 2, 14, 26, 38, 50, 62, …
So, the numbers that leave remainder 2 when divided by 3 and also remainder 2 when divided by 4 are 2, 14, 26, 38, 50, 62, …
All such numbers can be described by the algebraic expression 12k + 2.

5. “I hold some pebbles, not too many, When I group them in 3’s, one stays with me.
Try pairing them up — it simply won’t do, A stubborn odd pebble remains in my view.
Group them by 5, yet one’s still around, But grouping by seven, perfection is found.
More than one hundred would be far too bold, Can you tell me the number of pebbles I hold?”
See AnswerLet the number be N.
If we divide N by 2, the remainder is 1.
If we divide N by 3, the remainder is 1.
If we divide N by 5, the remainder is 1.
The LCM of 2, 3, 5 is 30.
So any number that gives remainder 1 with all three can be written as:
N = 30k + 1 for some whole number k.
Now, it is given that if we divide N by 7, the remainder is 0.
So, it is a multiple of 7. The largest multiple of 7 (less than 100) is 98.
Checking 98 with all conditions
98 ÷ 3 = 32 remainder 2
98 ÷ 2 = 45 remainder 0
98 ÷ 5 = 19 remainder 3
98 ÷ 7 = 14 remainder 0
So, it is not satisfying the condition. Now check the previous number, that is 91.
Checking 91 with all conditions
91 ÷ 3 = 30 remainder 1
91 ÷ 2 = 45 remainder 1
91 ÷ 5 = 18 remainder 1
91 ÷ 7 = 13 remainder 0
91 < 100
So, there are 91 pebbles.

6. Tathagat has written several numbers that leave a remainder of 2 when divided by 6. He claims, “If you add any three such numbers, the sum will always be a multiple of 6.” Is Tathagat’s claim true?
See AnswerIf a number that leave remainder 2 when divided by 6 look like 6k + 2.
Examples: 2, 8, 14, 20, 26, 32, 38, …
Let the three numbers be:
6a + 2
6b + 2
6c + 2
Their Sum = (6a + 2) + (6b + 2) + (6c + 2)
= 6(a + b + c) + 6
= 6(a + b + c + 1)
This expression is clearly a multiple of 6. There is no way to get a remainder.
So, if a number is of the form 6k + 2, then the sum of any three such numbers is always divisible by 6.

7. When divided by 7, the number 661 leaves a remainder of 3, and 4779 leaves a remainder of 5. Without calculating, can you say what remainders the following expressions will leave when divided by 7? Show the solution both algebraically and visually. (i) 4779 + 661 (ii) 4779 – 661
See Answer(i) 4779 + 661
If 4779 is divided by 7, the remainder is 5.
If 661 is divided by 7, the remainder is 3.
If we add them:
4779 + 661 leaves remainder 5+3 = 8, when divided by 7.
⇒ 4779 + 661 leaves remainder 1, when divided by 7. [as 8 ÷ 7 leaves remainder 1]
Hence, 4779 + 661 leaves remainder 1, when diveded by 7.
(ii) 4779 – 661
If 4779 is divided by 7, the remainder is 5.
If 661 is divided by 7, the remainder is 3.
If we subtract them:
4779 – 661 leaves remainder 5 – 3 = 2, when divided by 7.
Hence, 4779 – 661 leaves remainder 2, when diveded by 7.

8. Find a number that leaves a remainder of 2 when divided by 3, a remainder of 3 when divided by 4, and a remainder of 4 when divided by 5. What is the smallest such number? Can you give a simple explanation of why it is the smallest?
See AnswerGiven that:
The number leaves a remainder of 2 when divided by 3
The number leaves a remainder of 3 when divided by 4
The number leaves a remainder of 4 when divided by 5
These conditions mean:
N is 2 more than a multiple of 3: 3k + 2
N is 3 more than a multiple of 4: 4m + 3
N is 4 more than a multiple of 5: 5n + 4
But all three have the same form: multiple + (divisor – 1)
That means N is 1 less than multiples of 3, 4 and 5.
Because:
3k + 2 = (3k + 3) – 1
4m + 3 = (4m + 4) – 1
5n + 4 = (5n + 5) – 1
So N + 1 must be a common multiple of 3, 4 and 5.
Now, the LCM of 3, 4 and 5 is 60.
So the candidates for N + 1 are 60, 120, 180, …
Subtracting 1 to get N, we have
N + 1 = 60 ⇒ N = 59
N + 1 = 120 ⇒ N = 119
N + 1 = 180 ⇒ N = 179
The smallest number is 59.

Page 123

Similarly, explain using algebra why the divisibility shortcuts for 5, 2, 4, and 8 work.
See AnswerLet the number be: 1000d + 100c + 10b + a, where
a = units digit
b = tens digit
c = hundreds digit
d = thousands digit and so on.
All place-value terms except a contain a factor of 10.
► Divisibility by 5
A number is divisible by 5 if its units digit is 0 or 5.
Algebraic explanation: N = 10b + a (ignoring higher place values since all are multiples of 10)
So N = 5(2b) + a
This number is divisible by 5 only if a is also a multiple of 5, i.e., a = 0 or 5
A number is divisible by 5 if and only if its units digit is 0 or 5.
► Divisibility by 2
Algebraic explanation N = 10b + a
Since 10b is always even, the “even/odd nature” of N depends entirely on a.
If a is even ⇒ N is even ⇒ divisible by 2
If a is odd ⇒ N is odd ⇒ NOT divisible by 2
A number is divisible by 2 if and only if the units digit is even.
► Divisibility by 4
A number is divisible by 4 if the last two digits form a number divisible by 4.
Algebraic explanation N = 100c + 1000d + … + (10b + a)
100c, 1000d, … are all multiples of 100, hence multiples of 4.
So the only part that matters is 10b + a.
Let the last two-digit number be ab, i.e., 10b + a.
If 10b + a is divisible by 4, then the entire number N is divisible by 4.
A number is divisible by 4 if the number formed by its last two digits is divisible by 4.
► Divisibility by 8
A number is divisible by 8 if the last three digits form a number divisible by 8.
Algebraic explanation N = 1000d + 100c + 10b + a
1000d is a multiple of 1000 ⇒ divisible by 8
100c is a multiple of 100 ⇒ divisible by 4 and thus by 8.
Actually 100 is not divisible by 8, but 100c is divisible by 4, not necessarily by 8.
So we must include the hundreds digit in the small part.
Rewrite N: N = 1000k + (100c + 10b + a)
1000k is divisible by 8 for any integer k.
Thus, whether N is divisible by 8 depends only on 100c + 10b + a
That is exactly the number formed by the last three digits: cba.
So, a number is divisible by 8 if the number formed by its last three digits is divisible by 8.

Can you say, without actually calculating, which of these numbers are divisible by 9: 999, 909, 900, 90, 990?
See AnswerLet’s check each number by adding its digits.
► 999
Digit sum = 9 + 9 + 9 = 27
27 is divisible by 9.
⇒ 999 is divisible by 9
► 909
Digit sum = 9 + 0 + 9 = 18
18 is divisible by 9.
⇒ 909 is divisible by 9
► 900
Digit sum = 9 + 0 + 0 = 9
9 is divisible by 9.
⇒ 900 is divisible by 9
► 90
Digit sum = 9 + 0 = 9
9 is divisible by 9.
⇒ 90 is divisible by 9
► 990
Digit sum = 9 + 9 + 0 = 18
18 is divisible by 9.
⇒ 990 is divisible by 9

Page 124

Can we say that any number made up of only the digits ‘0’ and ‘9’, in any order, will always be divisible by 9?
See AnswerYes, it is always true.
Because a number is divisible by 9 if the sum of its digits is divisible by 9.
Now consider any number made only of 0’s and 9’s:
► Every 9 contributes 9 to the digit sum.
► Every 0 contributes 0.
So the total digit sum is: 9 + 9 + 9 + … + 0 + 0 + 0
This is always a multiple of 9.
Therefore, the number itself must be a multiple of 9.
Examples:
► 9 ⇒ sum = 9 ⇒ divisible by 9
► 90 ⇒ sum = 9 ⇒ divisible by 9
► 909 ⇒ sum = 18 ⇒ divisible by 9
► 9900 ⇒ sum = 18 ⇒ divisible by 9
► 999 ⇒ sum = 27 ⇒ divisible by 9
All divisible by 9.
Hence, any number made using only the digits ‘0’ and ‘9’ will ALWAYS be divisible by 9, because its digit sum is always a multiple of 9.

Is 10 divisible by 9? If not, what is the remainder?
See AnswerNo, 10 is not divisible by 9.
Here: 10 ÷ 9 = 1 remainder 1
So, if we divide 10 by 9 get remainder 1.

Similarly, look at the remainder when the multiples of 100 (100, 200, 300, … ) are divided by 9. What do you notice?
See AnswerChecking for each multiple of 100:
► 100
Digit sum = 1 and Remainder = 1
► 200
Digit sum = 2 and Remainder = 2
► 300
Digit sum = 3 and Remainder = 3
► 400
Digit sum = 4 and Remainder = 4
► 500
Digit sum = 5 and Remainder = 5
► 600
Digit sum = 6 and Remainder = 6
► 700
Digit sum = 7 and Remainder = 7
► 800
Digit sum = 8 and Remainder = 8
► 900
Digit sum = 9 and Remainder = 0
Because 900 is divisible by 9
► 1000
Digit sum = 1 and Remainder = 1
► 1100
Digit sum = 2 and Remainder = 2 …and the pattern repeats.
My observation:
The pattern of remainders is 1, 2, 3, 4, 5, 6, 7, 8, 0, 1, 2, 3, … It repeats every 9 steps.

Using this observation, find the remainder when 427 is divided by 9.
See Answer► 427
Digit sum = 4 + 2 + 7 = 13
It is greater than 9.
Subtracting 9 from 13, we get 13 – 9 = 4
So, the remainder = 4

Page 125

Will this work with bigger numbers?
See AnswerYes, the same pattern works for bigger numbers — and it always will.
We are looking at multiples of 100: 100, 200, 300, 400, 500, …, 1000, 1100, 1200, …
100 gives a remainder of 1 when divided by 9.
Because: 100 ÷ 9 = 11 remainder 1
This is true no matter how large the number becomes.
That means:
100 × 1 → remainder 1
100 × 2 → remainder 2
100 × 3 → remainder 3 …
100 × 8 → remainder 8
100 × 9 → remainder 0
100 × 10 → remainder 1
100 × 11 → remainder 2 and so on…
The pattern always repeats every 9 steps, no matter how big the numbers get.
Therefore, this works for ALL larger numbers and the pattern will always be 1, 2, 3, 4, 5, 6, 7, 8, 0, repeating forever.

Look at each of the following statements. Which are correct and why?
(i) If a number is divisible by 9, then the sum of its digits is divisible by 9.
(ii) If the sum of the digits of a number is divisible by 9, then the number is divisible by 9.
(iii) If a number is not divisible by 9, then the sum of its digits is not divisible by 9.
(iv) If the sum of the digits of a number is not divisible by 9, then the number is not divisible by 9.
See Answer(i) Correct
Because the divisibility rule for 9 works both ways: If a number is divisible by 9, the sum of its digits will also be divisible by 9.
Example: number = 729
Digit sum = 7 + 2 + 9 = 18 (divisible by 9)
(ii) Correct
Because this is exactly the rule for checking divisibility by 9.
Example: sum = 18 → divisible by 9
Number = 999 → divisible by 9
(iii) Correct
Because if the digit sum were divisible by 9, the number itself would be divisible by 9.
(iv) Correct
This is the reverse direction of (ii).
If the digit sum is NOT divisible by 9, then the number definitely CANNOT be divisible by 9.
Example:
Number = 245
Digit sum = 2 + 4 + 5 = 11 (not divisible by 9)
So, number is not divisible by 9.

Page 126

1. Find, without dividing, whether the following numbers are divisible by 9.
(i) 123 (ii) 405 (iii) 8888 (iv) 93547 (v) 358095
See AnswerA number is divisible by 9 if the sum of its digits is divisible by 9.
Check each number without dividing:
► (i) 123
Digits: 1 + 2 + 3 = 6, which is not divisible by 9.
So, 123 is not divisible by 9.
► (ii) 405
Digits: 4 + 0 + 5 = 9, which is divisible by 9.
So, 405 is divisible by 9.
► (iii) 8888
Digits: 8 + 8 + 8 + 8 = 32, which is not divisible by 9.
So, 8888 is not divisible by 9.
► (iv) 93547
Digits: 9 + 3 + 5 + 4 + 7 = 28, which is not divisible by 9.
So, 93547 is not divisible by 9.
► (v) 358095
Digits: 3 + 5 + 8 + 0 + 9 + 5 = 30, which is not divisible by 9.
So, 358095 is not divisible by 9.

2. Find the smallest multiple of 9 with no odd digits.
See AnswerThe smallest multiple of 9 with no odd digits is 288.
Sum of digit = 2 + 8 + 8 = 18, which is divisible by 9
So, 288 is divisible by 9.

3. Find the multiple of 9 that is closest to the number 6000.
See AnswerTo find the multiple of 9 closest to 6000, we do this:
9 × 600 = 5400
9 × 650 = 5850
9 × 660 = 5940
9 × 667 = 6003
9 × 666 = 5994
Now, 6000 lies between: 5994 (9 × 666) and 6003 (9 × 667)
Distance from 6000:
► |6000 – 5994| = 6
► |6003 – 6000| = 3
So, the closest multiple of 9 to 6000 is 6003.

4. How many multiples of 9 are there between the numbers 4300 and 4400?
See AnswerThe first multiple of 9 after 4300 is 4302.
The last multiple of 9 before 4400 is 4392.
Now counting multiples from 4302 to 4392:
Here,
4302 = 9 × 478
4392 = 9 × 488
So, the number of multiples: 488 − 478 + 1 = 11
Hence, there are 11 multiples of 9 between 4300 and 4400.

Page 126

The shortcut to find the divisibility by 3 is similar to the method for 9. A number is divisible by 3 if the sum of its digits is divisible by 3. Explore the remainders when powers of 10 are divided by 3. Explain why this method works.
See AnswerThe powers of 10 and their remainders when divided by 3:
10 ÷ 3 → remainder 1
100 ÷ 3 → remainder 1
1000 ÷ 3 → remainder 1
10000 ÷ 3 → remainder 1 and so on.
Observation: Every power of 10 leaves remainder 1 when divided by 3.
A number like abcd means: 1000a + 100b + 10c + d
Now replace powers of 10 with their remainders when divided by 3:
1000 → 1
100 → 1
10 → 1
1 → 1
So:
1000a → a
100b → b
10c → c
d → d
Adding them: a + b + c + d
Therefore, a number and the sum of its digits leave the same remainder when divided by 3.
Since both the number and the sum of its digits have the same remainder when divided by 3:
► If the digit sum is divisible by 3, the whole number is divisible by 3.
► If the digit sum is not divisible by 3, the whole number is not divisible by 3.
This is exactly the divisibility rule.

Page 127

Using these observations, can you tell whether the number 462 is divisible by 11?
See AnswerBreaking 462 into place values:
• 400 (hundreds digit 4)
• 60 (tens digit 6)
• 2 (units digit 2)
Finding each part’s relation to multiples of 11
• 400 is 4 more than a multiple of 11, so remainder = +4
• 60 is 6 less than a multiple of 11, so remainder = –6
• 2 is 2 more than a multiple of 11, so remainder = +2
Adding the remainders: (+4) + (–6) + (+2) = 0
A remainder of 0 means the number is exactly divisible by 11. So, 462 is divisible by 11.

What could be a general method or shortcut to check divisibility by 11?
See AnswerDivisibility Rule for 11:
► Take the difference of the sum of digits in odd places and the sum of digits in even places.
► If the difference is 0 or a multiple of 11, the number is divisible by 11.
This works for any number, whether 2 digits or 20 digits.
Example:
Checking if 462 is divisible by 11.
Digits: 4 6 2
Odd places (from right): 2, 4
Even place: 6
Calculate: (2 + 4) – (6) = 6 – 6 = 0
Since the result is 0, so 462 is divisible by 11.

Page 128

If this difference is 11 or a multiple of 11, what does that say about the remainder obtained when the number is divisible by 11?
See AnswerWhen we use the divisibility rule for 11, we take:
Difference = (sum of digits in odd places) – (sum of digits in even places)
This difference and the original number leave the same remainder when divided by 11.
So if the difference is 11, –11, 22, –22, 33, … then all of these are multiples of 11, which means the remainder obtained when dividing the number by 11 is 0.
So, the number is exactly divisible by 11.

Using this shortcut, find out whether the following numbers are divisible by 11. Further, find the remainder if the number is not divisible by 11.
(i) 158 (ii) 841 (iii) 481 (iv) 5529 (v) 90904 (vi) 857076
See Answer(i) 158
Odd places: 8, 1 → sum = 8 + 1 = 9
Even places: 5 → sum = 5
Difference = 9 – 5 = 4
So, not divisible and remainder = 4.
(ii) 841
Odd places: 1, 8 → sum = 1 + 8 = 9
Even places: 4 → sum = 4
Difference = 9 – 4 = 5
So, not divisible and remainder = 5.
(iii) 481
Odd places: 1, 4 → sum = 1 + 4 = 5
Even places: 8 → sum = 8
Difference = 8 – 5 = 3
So, not divisible and remainder = 3.
(iv) 5529
Odd places: 9, 5 → sum = 14
Even places: 2, 5 → sum = 7
Difference = 14 – 7 = 7
So, not divisible and remainder = 7.
(v) 90904
Odd places: 4, 9, 9 → sum = 22
Even places: 0, 0 → sum = 0
Difference = 22 – 0 = 22
So, it is divisible by 11.
(vi) 857076
Odd places: 6, 0, 5 → sum = 11
Even places: 7, 7, 8 → sum = 22
Difference = 22 – 11 = 11
Here, 11 is a multiple of 11.
So, it is divisible by 11.

Page 129

Is this method similar to or different from the method we saw just before?
See AnswerIt is actually the same method just written in a different way. Both methods are based on the same rule for divisibility by 11.

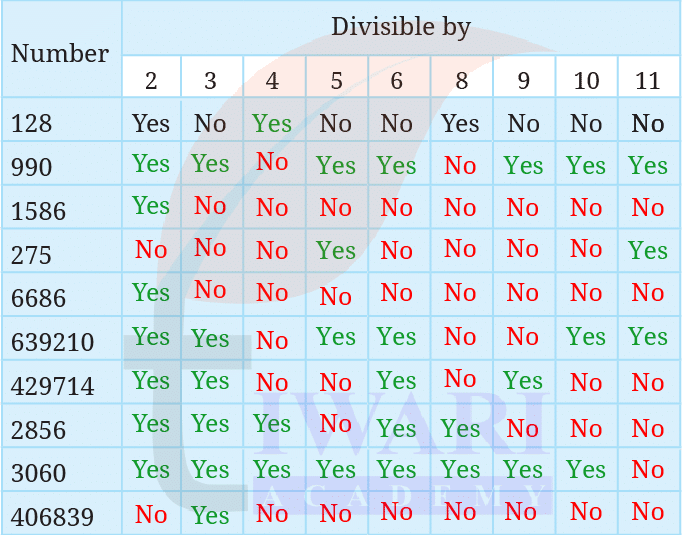
Fill in the following table. Find a quick way to do this?

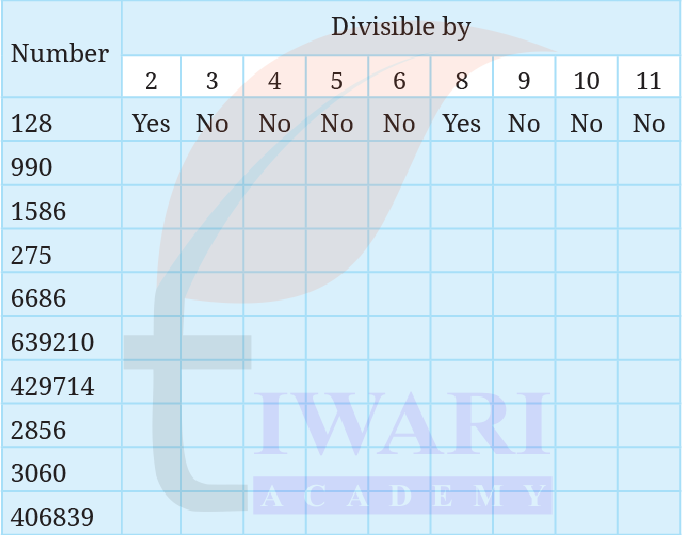
Answer:

How can we find out if a number is divisible by 6?
See AnswerA number is divisible by 6 if and only if:
It is divisible by 2 and it is divisible by 3.
Both conditions must be true.
► A number is divisible by 2 if its last digit is even: 0, 2, 4, 6, 8
► A number is divisible by 3 if the sum of its digits is divisible by 3.
Examples:
► 132
Last digit = 2 → divisible by 2
Digit sum = 1 + 3 + 2 = 6 → divisible by 3
So, 132 is divisible by 6
► 124
Last digit = 4 → divisible by 2
Digit sum = 1 + 2 + 4 = 7 → not divisible by 3
So, 124 is not divisible by 6
Hence, a number is divisible by 6 if it is divisible by both 2 and 3.

Will checking its divisibility by its factors 2 and 3 work? Use the shortcuts for 2 and 3 on these numbers and divide each number by 6 to verify — 38, 225, 186, 64.
See AnswerYes. To check if a number is divisible by 6, we only need to check:
• Divisible by 2 (last digit even)
• Divisible by 3 (digit sum divisible by 3)
If both are true → the number is divisible by 6.
Applying this shortcut to the numbers: 38, 225, 186, 64
► 38
Last digit = 8 → even → divisible by 2
Digit sum = 3 + 8 = 11 → not divisible by 3
So, 38 is not divisible by 6.
► 225
Last digit = 5 → odd → not divisible by 2
Digit sum = 2 + 2 + 5 = 9 → divisible by 3
So, 225 is not divisible by 6.
► 186
Last digit = 6 → even → divisible by 2
Digit sum = 1 + 8 + 6 = 15 → 15 divisible by 3
So, 186 is divisible by 6.
► 64
Last digit = 4 → even → divisible by 2
Digit sum = 6 + 4 = 10 → not divisible by 3
So, 64 is not divisible by 6.

Page 130

How about checking divisibility by 24? Will checking the divisibility by its factors, 4 and 6, work? Why or why not?
See AnswerNo, because there in a common factor 2 between 4 and 6.
Examples:
► 12
12 ÷ 4 = 3 → divisible
12 ÷ 6 = 2 → divisible
But 12 ÷ 24 → not divisible.
Here, 12 is not a multiple of 24, even though it is divisible by both 4 and 6.
This proves the method does not work.
Correct method to check divisibility by 24: A number is divisible by 24 only if:
✔ It is divisible by 8 (means last 3 digits divisible by 8)
✔ AND divisible by 3 (digit sum divisible by 3)
Because: 24 = 8 × 3 and there is no common factor between 3 and 8.

What property do you think this digital root will have? Recall that we did this while finding the divisibility shortcut for 9.
See AnswerThe digital root is the same as the remainder obtained when the number is divided by 9.
This means if a number has digital root 9, then the number is divisible by 9. If a number has digital root 2, the number leaves remainder 2 when divided by 9.
The digital root of a number always gives the same remainder that the number leaves when divided by 9.
If the digital root is 9 (or 0), the number is divisible by 9.

Between the numbers 600 and 700, which numbers have the digital root: (i) 5, (ii) 7, (iii) 3?
See AnswerTo find numbers between 600 and 700 with a given digital root, we use the key fact:
Digital root = remainder when divided by 9 (except remainder 0 → digital root 9).
The digital root of 600
Digits: 6 + 0 + 0 = 6
This means:
600 → digital root 6
601 → digital root 7
602 → digital root 8
603 → digital root 9
604 → digital root 1
605 → digital root 2
606 → digital root 3
607 → digital root 4
608 → digital root 5
609 → digital root 6
610 → digital root 7
611 → digital root 8
612 → digital root 9 … (pattern repeats every 9)
So every block of 9 numbers repeats the cycle: 6, 7, 8, 9, 1, 2, 3, 4, 5
(i) Digital root = 5
In each 9-number cycle, digital root 5 appears at the 9th position.
From above:
608 → digital root 5
Next cycle: +9
So, the numbers: 617, 626, 635, 644, 653, 662, 671, 680, 689, 698
Numbers between 600 – 700 with digital root = 5: 608, 617, 626, 635, 644, 653, 662, 671, 680, 689, 698.
(ii) Digital root = 7
Digital root 7 appears at the 2nd position in each cycle.
From above: 601, 610, 619, 628, 637, 646, 655, 664, 673, 682, 691, 699.
Numbers between 600 – 700 with digital root = 7: 601, 610, 619, 628, 637, 646, 655, 664, 673, 682, 691, 699.
(iii) Digital root = 3
Digital root 3 appears at the 7th position.
From above: 606, 615, 624, 633, 642, 651, 660, 669, 678, 687, 696
Numbers between 600 – 700 with digital root = 3: 606, 615, 624, 633, 642, 651, 660, 669, 678, 687, 696.

Write the digital roots of any 12 consecutive numbers. What do you observe?
See AnswerThe digital roots of any 12 consecutive numbers. For example, take the numbers from 245 to 256. The digital root of the numbers:
245 → 2
246 → 3
247 → 4
248 → 5
249 → 6
250 → 7
251 → 8
252 → 9
253 → 1
254 → 2
255 → 3
256 → 4
Digital roots: 2, 3, 4, 5, 6, 7, 8, 9, 1, 2, 3, 4
Observation: The digital roots follow a repeating cycle of length 9. They go in the sequence 1, 2, 3, 4, 5, 6, 7, 8, 9 and then repeat again. So in any 12 consecutive numbers, we see one full cycle (1 to 9) and then the next cycle begins (1, 2, 3, …).

Now, find the digital roots of some consecutive multiples of (i) 3, (ii) 4, and (iii) 6.
See Answer(i) Digital roots of consecutive multiples of 3
Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30
So, the digital roots:
3 → 3
6 → 6
9 → 9
12 → 1+2 = 3
15 → 1+5 = 6
18 → 1+8 = 9
21 → 2+1 = 3
24 → 2+4 = 6
27 → 2+7 = 9
30 → 3+0 = 3
Digital roots: 3, 6, 9, 3, 6, 9, 3, 6, 9, 3
Observation: Digital roots repeat in a cycle: 3, 6, 9, 3, 6, 9, …
(ii) Digital roots of consecutive multiples of 4
Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40
So, the digital roots:
4 → 4
8 → 8
12 → 3
16 → 7
20 → 2
24 → 6
28 → 1
32 → 5
36 → 9
40 → 4
Digital roots: 4, 8, 3, 7, 2, 6, 1, 5, 9, 4
Observation: The pattern cycles every 9 numbers because digital roots repeat.
(iii) Digital roots of consecutive multiples of 6
Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60
So, the digital roots:
6 → 6
12 → 1+2 = 3
18 → 1+8 = 9
24 → 2+4 = 6
30 → 3+0 = 3
36 → 3+6 = 9
42 → 4+2 = 6
48 → 4+8 = 12 → 1+2 = 3
54 → 5+4 = 9
60 → 6+0 = 6
Digital roots: 6, 3, 9, 6, 3, 9, 6, 3, 9, 6
Observation: Digital roots repeat in a cycle: 6, 3, 9, 6, 3, 9, …

What are the digital roots of numbers that are 1 more than a multiple of 6? What do you notice?
See AnswerWe want the digital roots of numbers that are 1 more than a multiple of 6.
Such numbers look like: 6k + 1
Therefore the numbers:
6×1 + 1 = 7
6×2 + 1 = 13
6×3 + 1 = 19
6×4 + 1 = 25
6×5 + 1 = 31
6×6 + 1 = 37
6×7 + 1 = 43
6×8 + 1 = 49
6×9 + 1 = 55
6×10 + 1 = 61
Now their digital roots:
7 → 7
13 → 1+3 = 4
19 → 1+9 = 10 → 1+0 = 1
25 → 2+5 = 7
31 → 3+1 = 4
37 → 3+7 = 10 → 1
43 → 4+3 = 7
49 → 4+9 = 13 → 1+3 = 4
55 → 5+5 = 10 → 1
61 → 6+1 = 7
Digital roots: 7, 4, 1, 7, 4, 1, 7, 4, 1, 7
Observation: The digital roots follow a repeating cycle: 7 → 4 → 1 → 7 → 4 → 1 → …
Hence. numbers that are 1 more than a multiple of 6 always have digital roots repeating in the pattern: 7, 4, 1, 7, 4, 1, …

I’m made of digits, each tiniest and odd, No shared ground with root #1 — how odd!
See AnswerGiven that: “I’m made of digits, each tiniest and odd”
The smallest odd digits → 1, 3, 5, 7, 9
The smallest odd primes → 3, 5, 7
These may be the “tiniest odd primes”.
Now given that: “No shared ground with root #1 — how odd!”
So we need a number made of 3, 5, 7 whose digital root ≠ 1.
The simplest one: 357
Sum = 3 + 5 + 7 = 15
Digital root = 1 + 5 = 6
This is not equal to 1 and it uses only odd prime digits (3, 5, 7).
So it satisfies the whole riddle.

Page 131

1. The digital root of an 8-digit number is 5. What will be the digital root of 10 more than that number?
See AnswerLet the 8-digit number be N.
Given that the digital root of N = 5
The new number: N + 10
Now, we have to find the digital root of N + 10, without knowing the actual number.
Adding 10 to a number affects only the tens digit and units digit. It means +10 → increases the digit sum by 1.
(Adding 10 means adding 1 ten and 0 ones → total digit-sum increase = 1.)
So, digit sum of (N + 10) = digit sum of N + 1
Therefore, digital root(N + 10) = digital root(5 + 1) = digital root(6) = 6

2. Write any number. Generate a sequence of numbers by repeatedly adding 11. What would be the digital roots of this sequence of numbers? Share your observations.
See AnswerWriting any number and adding 11 again and again gives a sequence:
N,
N + 11,
N + 22,
N + 33,
N + 44, …
Let the digital root of N be DR(N).
Now look at how digital roots change when we add 11.
Since 11 = 1 + 1, adding 11 increases the digit sum by 2.
Therefore:
DR(N + 11) = DR(N) + 2
DR(N + 22) = DR(N) + 4
DR(N + 33) = DR(N) + 6
DR(N + 44) = DR(N) + 8
DR(N + 55) = DR(N) + 10 → DR(N) + 1 …
The digital roots form a repeating cycle with step-size 2.
Example: Let N = 37
DR(37) = 3 + 7 = 10 → 1
Sequence: 37, 48, 59, 70, 81, 92, 103, …
Digital roots: 1, 3, 5, 7, 9, 2, 4, 6, 8, 1, …
Observation: The digital roots increase by 2 each time.
So the pattern is a cycle of 1 → 3 → 5 → 7 → 9 → 2 → 4 → 6 → 8 → 1 → …
Conclusion: Whenever you repeatedly add 11, the digital roots form a repeating cycle that moves forward by 2 each step.

3. What will be the digital root of the number 9a + 36b + 13?
See AnswerWe know that the digital root is the remainder when the number is divided by 9 (with 0 replaced by 9).
Step 1: Reducing each term:
► 9a
9a is always divisible by 9
⇒ remainder = 0
⇒ contributes 0 to digital root
► 36b
36 = 9 × 4
⇒ also divisible by 9
⇒ remainder = 0
⇒ contributes 0
► 13
If 13 is divided by 9, the remainder = 4 (because 13 = 9 + 4)
⇒ contributes 4
Now, adding the remainders: 0 + 0 + 4 = 4
Therefore, the digital root of 9a + 36b + 13 is 4.

4. Make conjectures by examining if there are any patterns or relations between
(i) the parity of a number and its digital root.
See AnswerParity means whether a number is even or odd.
Let’s test the pattern: Digital root of an even number can be odd or even.
Example:
24 → digital root = 6 (even)
18 → digital root = 9 (odd)
Digital root of an odd number is always odd.
Example:
17 → digital root = 8 → digital root = 8 (even)? No—let’s check correctly:
1 + 7 = 8 → 8 (even!)
So this gives a clue: digital roots of odd numbers may be even too.
Let’s examine more: For Odd numbers:
15 → digital root = 6 (even)
19 → digital root = 1 (odd)
35 → digital root = 8 (even)
Observation: Digital roots of odd numbers can be even OR odd.
Therefore, there is no fixed relationship between parity and digital root.
► Even numbers may have even or odd digital roots.
► Odd numbers may have even or odd digital roots.

(ii) the digital root of a number and the remainder obtained when the number is divided by 3 or 9.
See AnswerThis one has a very clear and strong pattern: Relation with remainder when divided by 9.
The digital root is exactly the remainder of the number when divided by 9, except that remainder 0 is written as 9.
Example:
Number = 47
digital root = 4 + 7 = 11 → digital root = 2
47 ÷ 9 → remainder = 2
So, digital root ≡ number (when divided by 9)
Relation with remainder when divided by 3: If the digital root is divisible by 3, then the number is divisible by 3.
Digital roots divisible by 3 are: 3, 6, 9
Examples:
digital root = 3 → number divisible by 3
digital root = 6 → number divisible by 3
digital root = 9 → number divisible by 3
Therefore, the digital root of a number gives the same remainder the number gives when divided by 9.
► If the digital root is 3, 6, or 9, then the number is divisible by 3.
► If the digital root is 9 (or 0 mod 9), the number is divisible by 9.

Page 131

Solve the cryptarithms given below.

See Answer(i) A1 + 1B = B0
⇒ 10A + 1 + 10 + B = 10B
⇒ 10A + 11 = 9B
Only solution in digits: A = 7, B = 9
So, 71 + 19 = 90
(ii) AB + 37 = 6A
⇒ 10A + B + 37 = 60 + A
⇒ 9A + B = 23
Only solution: A = 2, B = 5
So, 25 + 37 = 62
(iii) ON + ON + ON = PO
This gives three valid solutions:
► ON = 17, PO = 51 → 17 + 17 + 17 = 51
► ON = 24, PO = 72 → 24 + 24 + 24 = 72
► ON = 31, PO = 93 → 31 + 31 + 31 = 93
(iv) QR + QR + QR = PRR
Unique solution: Q = 8, R = 5, P = 2
So, 85 + 85 + 85 = 255

(v) PQ × 8 = RS.
See AnswerEach letter stands for a single digit (0–9) and P ≠ 0 (since PQ is a 2-digit number).
So, (10P + Q) × 8 = 10R + S
We just need to find PQ such that multiplying it by 8 gives another 2-digit number RS.
PQ must be between 12 and 99 so that RS is still 2 digits after multiplying by 8.
When multiplying by 8, the product must be < 100: 8 × PQ < 100 ⇒ PQ < 12.5
So the only possible values of PQ (two-digit numbers) are PQ = 12.
Therefore, 12 × 8 = 96, which is two digits.
So, P = 1, Q = 2, R = 9 and S = 6.

Page 132

(vi) Try this now: GH × H = 9K.
See AnswerHere, GH × H = 9K
Where, GH is a 2-digit number ⇒ 10G+H and H is a single digit.
9K is a 2-digit number beginning with 9.
All letters represent digits and G ≠ 0.
So the equation is (10G + H) × H = 90 + K
We have to find digits G, H, K that satisfy this.
Since GH × H must produce a number in the 90s, we have to try all values of H such that multiplying yields something between 90 and 99.
Testing values of H = 1 to 9.
► Case H = 9
GH × 9 = 9K must be between 90–99.
Let GH = something ending with 9.
So, 19 × 9 = 171 → too big
29 × 9 = 261 → too big
… all will exceed 100.
So H = 9 is impossible.
► Case H = 8
GH × 8 = 9K (must be 90–99)
Trying GH values ending with 8:
18 × 8 = 144 → no
28 × 8 = 224 → no
38 × 8 = 304 → no
48 × 8 = 384 → no
58 × 8 = 464 → no
68 × 8 = 544 → no
78 × 8 = 624 → no
88 × 8 = 704 → no
None give a number in the 90s → H ≠ 8.
► Case H = 7
Try GH × 7 = 9K:
Testing GH ending with 7:
17 × 7 = 119 → no
27 × 7 = 189 → no
37 × 7 = 259 → no
47 × 7 = 329 → no
57 × 7 = 399 → no
67 × 7 = 469 → no
77 × 7 = 539 → no
87 × 7 = 609 → no
None fall within 90–99 → H ≠ 7.
► Case H = 6
GH × 6 must be in the 90s.
Checking GH ending with 6:
16 × 6 = 96 → Yes.
So, GH = 16 and H = 6
⇒ 16 × 6 = 96 = 9K ⇒ K = 6
Possible solution: G = 1, H = 6 and K = 6.

(vii) Here is one more: BYE × 6 = RAY.
See AnswerEach letter is a digit. Same letter → same digit. Different letters → different digits.
Since BYE is a 3-digit number, B must be 1 (because 2×6=12 already gives a 2-digit carry).
So B = 1.
► For the units place: 6 × E = a number ending in Y.
Trying E = 5: 6×5 = 30 → units digit = 0 → Y = 0, carry = 3.
► For the tens place: 6×Y + carry = A
Here Y = 0, carry = 3: 6×0 + 3 = 3 → A = 3, no new carry.
► For the hundreds place: 6×B + carry = R
⇒ 6×1 + 0 = 6 → R = 6.
Now we have: B = 1, Y = 0, E = 5, A = 3 and R = 6.
All digits are different, so it is valid.
So, the answer is 105 × 6 = 630.

What can you say about ‘Y’? What digits are possible/not possible?
See AnswerY is the units digit of BYE × 6 and also the tens digit of RAY.
From the units place: 6 × E = …Y
If we look at 6 times any digit:
6×0 = 0
6×1 = 6
6×2 = 12 → 2
6×3 = 18 → 8
6×4 = 24 → 4
6×5 = 30 → 0
6×6 = 36 → 6
6×7 = 42 → 2
6×8 = 48 → 8
6×9 = 54 → 4
So the last digit (Y) can only be 0, 2, 4, 6 or 8.

Solve the following:
(i) UT × 3 = PUT
See AnswerLet UT be the 2–digit number 10U + T.
⇒ (10U + T) × 3 = 100P + 10U + T
⇒ 30U + 3T = 100P + 10U + T
⇒ 20U + 2T = 100P
⇒ 10U + T = 50P
But 10U + T is exactly the number UT.
So UT = 50P.
UT is a 2–digit number, so 50P must be between 10 and 99.
Trying P = 1 → 50 × 1 = 50
P = 2 → 100 (3 digits, not allowed)
So P = 1, UT = 50 → U = 5, T = 0.
Checking 50 × 3 = 150 → PUT = 150 → P = 1, U = 5,T = 0 correct.
So, the answer is 50 × 3 = 150.

(ii) AB × 5 = BC
See AnswerLet AB = 10A + B, BC = 10B + C.
⇒ (10A + B) × 5 = 10B + C
⇒ 50A + 5B = 10B + C
⇒ 50A – 5B = C
C must be a digit from 0 to 9. So 50A – 5B is between 0 and 9.
Divide by 5: 10A – B is between 0 and 1.8, so possible values: 10A – B = 0 or 1.
⇒ 10A – B = 0 → B = 10A (impossible, B is 0–9, A at least 1)
Now, 10A – B = 1 → B = 10A – 1
Now B must be a digit 0–9.
Trying A = 1 → B = 9
Then C = 50A – 5B = 50 – 45 = 5, so AB = 19, BC = 95.
Checking: 19 × 5 = 95 correct.
So, the answer is 19 × 5 = 95.

(iii) L2N × 2 = 2NP
See AnswerNumber L2N = 100L + 20 + N
⇒ Number 2NP = 200 + 10N + P
Equation: 2 × (100L + 20 + N) = 200 + 10N + P
⇒ 200L + 40 + 2N = 200 + 10N + P
⇒ 200(L – 1) + 40 – 8N = P
P must be between 0 and 9.
Trying L = 1 first (otherwise 200 (L – 1) is already too big):
Then P = 40 – 8N. P between 0 and 9 gives:
40 – 8N ≥ 0 → N ≤ 5
⇒ 40 – 8N ≤ 9 → N ≥ 4
So N can be 4 or 5.
If N = 4 → P = 40 – 32 = 8 → L2N = 124, 124 × 2 = 248 = 2NP (N = 4, P = 8)
If N = 5 → P = 40 – 40 = 0 → L2N = 125, 125 × 2 = 250 = 2NP (N = 5, P = 0)
So, the answers:
► 124 × 2 = 248
► 125 × 2 = 250

(iv) XY × 4 = ZX
See AnswerLet XY = 10X + Y, ZX = 10Z + X.
⇒ (10X + Y) × 4 = 10Z + X
⇒ 40X + 4Y = 10Z + X
⇒ 39X + 4Y = 10Z
Now trying digits. XY × 4 must still be 2–digit, so XY ≤ 24.
Quick checking gives: X = 2, Y = 3 → XY = 23
⇒ 23 × 4 = 92 → ZX = 92 → Z = 9, X = 2, Y = 3 all different.
So, the answer is 23 × 4 = 92.

(v) PP × QQ = PRP
See AnswerNumber PP = 11P, number QQ = 11Q, number PRP = 100P + 10R + P.
⇒ (11P) × (11Q) = 100P + 10R + P
⇒ 121PQ = 101P + 10R
We just try digits P and Q (P, Q not zero, P≠Q) and check if the product looks like PRP:
Computing:
P = 2, Q = 1 → 22 × 11 = 242 → PRP = 242 → P=2, R=4
P = 3, Q = 1 → 33 × 11 = 363 → P=3, R=6
P = 4, Q = 1 → 44 × 11 = 484 → P=4, R=8
In each, letters are distinct.
So we get three valid solutions:
► 22 × 11 = 242
► 33 × 11 = 363
► 44 × 11 = 484

(vi) JK × 6 = KKK
See AnswerNumber JK = 10J + K, number KKK = 111K.
⇒ (10J + K) × 6 = 111K
⇒ 60J + 6K = 111K
⇒ 60J = 105K
⇒ 12J = 21K
⇒ 4J = 7K
J and K are digits, J ≠ 0.
⇒ 4J = 7K → J must be a multiple of 7.
Trying J = 7 → 4×7 = 28 = 7K → K = 4
So JK = 74, KKK = 444.
So, the answer is 74 × 6 = 444.

Page 132

Figure it Out
1. If 31z5 is a multiple of 9, where z is a digit, what is the value of z? Explain why there are two answers to this problem.
See AnswerWe want the number 31z5 to be a multiple of 9.
For divisibility by 9, the sum of digits must be a multiple of 9.
Sum of digits: 3 + 1 + z + 5 = 9 + z
So we need: 9 + z = 9 or 18 or 27 …
► Case 1: 9 + z = 9 → z = 0
► Case 2: 9 + z = 18 → z = 9
Next value would be 27 → z = 18 (not possible, since a digit is 0–9)
So the possible values of z are 0 and 9.
There are two answer because the known digits (3, 1, 5) already add up to 9, which is itself a multiple of 9.
► Adding z = 0 keeps the sum 9 (divisible by 9).
► Adding z = 9 makes the sum 18 (also divisible by 9).
Therefore, z can be either 0 or 9.

2. “I take a number that leaves a remainder of 8 when divided by 12. I take another number which is 4 short of a multiple of 12. Their sum will always be a multiple of 8”, claims Snehal. Examine his claim and justify your conclusion.
See AnswerLet the first number be 12a + 8 (since remainder is 8 when divided by 12)
Let the second number be 12b – 4 (since it is 4 less than a multiple of 12)
Now add them: (12a + 8) + (12b – 4)
= 12a + 12b + 4
= 12(a + b) + 4
So the sum is a multiple of 12 plus 4.
Now check remainder when this sum is divided by 8:
If 12 is divided by 8, the remainder is 4.
So, if 12(a + b) + 4 is divided by 8, the remainder is 4.
This is not always 0, so the sum is not always a multiple of 8.
Hence, Snehal’s claim is false. The sum does not always become a multiple of 8.

3. When is the sum of two multiples of 3, a multiple of 6 and when is it not? Explain the different possible cases, and generalise the pattern.
See AnswerLet the two numbers be 3a and 3b (where a and b are whole numbers)
Their sum is 3a + 3b = 3(a + b)
So the sum is always a multiple of 3.
But we have to check when is it a multiple of 6.
A number is a multiple of 6 if it is a multiple of 3 and even.
We already know the sum is a multiple of 3. So we only need to check “Is 3(a + b) even?”
Since 3 is odd, 3(a + b) is even ⇔ (a + b) is even.
► Case 1: Both a and b are even
– Then a + b is even.
– 3(a + b) is even and a multiple of 3 → multiple of 6.
Example:
3a = 6 (a = 2, even)
3b = 12 (b = 4, even)
Sum = 6 + 12 = 18 → 18 ÷ 6 = 3 → multiple of 6.
► Case 2: Both a and b are odd
– Then a + b is even (odd + odd = even).
– 3(a + b) is even → multiple of 6.
Example:
3a = 9 (a = 3, odd)
3b = 15 (b = 5, odd)
Sum = 9 + 15 = 24 → 24 ÷ 6 = 4 → multiple of 6.
► Case 3: One of a, b is even and the other is odd
– Then a + b is odd (even + odd = odd).
– 3(a + b) is odd → not a multiple of 6 (though still a multiple of 3).
Example:
3a = 6 (a = 2, even)
3b = 9 (b = 3, odd)
Sum = 6 + 9 = 15 → 15 ÷ 6 is not a whole number → not a multiple of 6.
General pattern (summary):
The sum of two multiples of 3 is a multiple of 6 exactly when both multiples are of the same “type”:
• both are even multiples of 3 (like 6, 12, 18, …), or
• both are odd multiples of 3 (like 3, 9, 15, 21, …).
If one multiple of 3 is even and the other is odd, their sum is a multiple of 3 but not a multiple of 6.

4. Sreelatha says, “I have a number that is divisible by 9. If I reverse its digits, it will still be divisible by 9”.
(i) Examine if her conjecture is true for any multiple of 9.
(ii) Are any other digit shuffles possible such that the number formed is still a multiple of 9?
See Answer(i) She says: “My number is divisible by 9. If I reverse its digits, it is still divisible by 9.”
We know that a number is divisible by 9 ⇔ sum of its digits is divisible by 9.
Reversing the digits does not change the digits themselves, so the digit sum stays the same.
Example:
18 → 1+8 = 9 → divisible by 9
Reverse: 81 → 8+1 = 9 → divisible by 9
342 → 3+4+2 = 9 → divisible by 9
Reverse: 243 → 2+4+3 = 9 → divisible by 9
Therefore, yes, the conjecture is always true for any multiple of 9. Reversing the digits keeps the same digit sum, so the reversed number is still divisible by 9.
(ii) Yes.
Any rearrangement (shuffle) of the digits keeps the same digits. So the sum of digits does not change.
If the original number is divisible by 9, then any rearrangement of the digits will also have the same digit sum and therefore will also be divisible by 9.
Example: Number = 378 → digit sum = 3+7+8 = 18 (multiple of 9)
All of these are also divisible by 9: 378, 738, 873, 837, 783, 387
Hence, any reordering (shuffling) of digits keeps the digit sum unchanged. So every arrangement of a number divisible by 9 is also divisible by 9.

5. If 48a23b is a multiple of 18, list all possible pairs of values for a and b.
See AnswerWe want the number 48a23b to be a multiple of 18.
A number is divisible by 18 if it is divisible by 2 and by 9.
Divisibility by 2:
The last digit b must be even. So b may be any number 0, 2, 4, 6, 8.
Divisibility by 9:
The sum of digits must be a multiple of 9.
Digit sum = 4 + 8 + a + 2 + 3 + b = 17 + a + b
So we need: 17 + a + b = 18 or 27 (36 is too large for digit values).
► Case 1: 17 + a + b = 18
⇒ a + b = 1
Since b is even, the only solution is b = 0 → a = 1
Pair: (a, b) = (1, 0)
► Case 2: 17 + a + b = 27
⇒ a + b = 10
Trying even b-values:
b = 2 → a = 8
b = 4 → a = 6
b = 6 → a = 4
b = 8 → a = 2
So, the list of all valid (a, b) pairs are (1, 0), (8, 2), (6, 4), (4, 6) and (2, 8).

6. If 3p7q8 is divisible by 44, list all possible pairs of values for p and q.
See Answer44 = 4 × 11, so the number must be divisible by 4 and by 11.
► Divisibility by 4:
A number is divisible by 4 if its last two digits form a number divisible by 4.
Last two digits are q8. So the number 10q + 8 must be divisible by 4.
Checking possible values of q:
q = 0 → 08 = 8 (divisible by 4)
q = 2 → 28 (divisible by 4)
q = 4 → 48 (divisible by 4)
q = 6 → 68 (divisible by 4)
q = 8 → 88 (divisible by 4)
So q can be: 0, 2, 4, 6, 8.
► Divisibility by 11:
For a 5-digit number abcde, the rule is (a + c + e) − (b + d) must be 0 or ±11.
Here the digits are a = 3, b = p, c = 7, d = q, e = 8
Now: (a + c + e) = 3 + 7 + 8 = 18 and (b + d) = p + q
So, 18 − (p + q) must be 0 or ±11.
Since p and q are digits, p + q is between 0 and 17.
So only possible is:
18 − (p + q) = 0 → p + q = 18 (impossible since max p+q = 9+8 = 17)
or
18 − (p + q) = 11 → p + q = 7
(We ignore −11 because that would give p+q = 29, not possible.)
Thus p + q = 7
Now from the both conditions: q is any number from 0, 2, 4, 6, 8 and and p + q = 7 → p = 7 − q
Checking each q:
q = 0 → p = 7 → pair (p, q) = (7, 0)
q = 2 → p = 5 → pair (5, 2)
q = 4 → p = 3 → pair (3, 4)
q = 6 → p = 1 → pair (1, 6)
q = 8 → p = −1 (not a digit, reject)
Therefore, all possible (p, q) pairs are (7, 0), (5, 2), (3, 4) and (1, 6).

7. Find three consecutive numbers such that the first number is a multiple of 2, the second number is a multiple of 3, and the third number is a multiple of 4.
Are there more such numbers? How often do they occur?
See AnswerLet the three numbers be n, n + 1, n + 2
► Third is a multiple of 4
Third number = n + 2 is a multiple of 4.
So n is 2 less than a multiple of 4.
Let’s list numbers that are 2 less than a multiple of 4:
Multiples of 4: 4, 8, 12, 16, 20, 24, 28, …
Subtract 2 from each: 2, 6, 10, 14, 18, 22, 26, …
So n must be one of: 2, 6, 10, 14, 18, 22, 26, … …[i]
► Second is a multiple of 3
Second number = n + 1 is a multiple of 3.
So n is 1 less than a multiple of 3.
Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, …
Subtract 1 from each: 2, 5, 8, 11, 14, 17, 20, 23, 26, …
So n must be one of 2, 5, 8, 11, 14, 17, 20, 23, 26, … …[ii]
Taking common numbers from [i] and [ii], we get the possible values of n: 2, 14, 26, 38, …
If n = 2 → numbers: 2, 3, 4
If n = 14 → numbers: 14, 15, 16
If n = 26 → numbers: 26, 27, 28
If n = 38 → numbers: 38, 39, 40
So one answer: 2, 3, 4, but there are many more.
The three consecutive numbers are always of the form: (12k + 2), (12k + 3), (12k + 4) for k = 0, 1, 2, 3, …
These special triples occur every 12 numbers.

8. Write five multiples of 36 between 45,000 and 47,000. Share your approach with the class.
See AnswerWe have to find five multiples of 36 between 45,000 and 47,000.
45000 ÷ 36 = 1250 (since 36 × 1250 = 45000 exactly)
So the first multiple is 45000.
By adding 36:
45000 + 36 = 45036
45036 + 36 = 45072
45072 + 36 = 45108
45108 + 36 = 45144
45144 + 36 = 45180 … all the way until we stay below 47000.
Five multiples between 45000 and 47000: 45036, 45072, 45108, 45144, 45180.

9. The middle number in the sequence of 5 consecutive even numbers is 5p. Express the other four numbers in sequence in terms of p.
See AnswerOut of 5 consecutive even numbers, the middle number is 5p.
Since these are even numbers, each number differs by 2.
So two numbers before 5p: 5p − 4 and 5p − 2.
Middle number: 5p
Two numbers after 5p: 5p + 2 and 5p + 4.
Therefore, 5 consecutive even numbers 5p − 4, 5p − 2, 5p, 5p + 2 and 5p + 4.

10. Write a 6-digit number that it is divisible by 15, such that when the digits are reversed, it is divisible by 6.
See AnswerThe 6-digit number is divisible by 15. A number divisible by 15 must be divisible by:
3 (digit sum divisible by 3) and 5 (last digit must be 0 or 5)
So the last digit of our 6-digit number must be 0 or 5.
Now, reversed number must be divisible by 6. We know that a number divisible by 6 must be divisible by: 2 (even) and 3 (digit sum divisible by 3).
So the first digit of the original number (which becomes the last digit after reversing)
must be even.
Let us try a simple number with first digit even: 2
Last digit = 0 (to make original number divisible by 5)
For example: 234150
Check original number: Digit sum = 2+3+4+1+5+0 = 15 → divisible by 3
Last digit = 0 → divisible by 5
So 234150 is divisible by 15.
Reverse the digits: 051432 = 51432
Check reversed number: Last digit = 2 → even
Digit sum = 5+1+4+3+2 = 15 → divisible by 3
So 51432 is divisible by 6.
Therefore the answer is 234150.

11. Deepak claims, “There are some multiples of 11 which, when doubled, are still multiples of 11. But other multiples of 11 don’t remain multiples of 11 when doubled”. Examine if his conjecture is true; explain your conclusion.
See AnswerTaking any multiple of 11: 11, 22, 33, 44, 55, 66, 77, 88, 99, …
Now double each one:
11 → 22
22 → 44
33 → 66
44 → 88
55 → 110
66 → 132
77 → 154
88 → 176
99 → 198
All of these results are also multiples of 11.
(We can check by dividing each number by 11.)
General explanation: Any multiple of 11 can be written as 11 × n.
When we double it, we get 2 × (11 × n) = 22 × n
This is clearly 11 × (2n), which is again a multiple of 11.
So, Deepak’s conjecture is false. All multiples of 11 remain multiples of 11 when doubled.
There is no exception.

12. Determine whether the statements below are ‘Always True’, ‘Sometimes True’, or ‘Never True’. Explain your reasoning.
(i) The product of a multiple of 6 and a multiple of 3 is a multiple of 9.
(ii) The sum of three consecutive even numbers will be divisible by 6.
(iii) If abcdef is a multiple of 6, then badcef will be a multiple of 6.
(iv) 8 (7b – 3) – 4 (11b + 1) is a multiple of 12.
See Answer(i) Let the numbers be:
multiple of 6 = 6a
multiple of 3 = 3b
Product = 6a × 3b = 18ab = 9 × (2ab)
Since 18ab is 9 times some whole number, it is always a multiple of 9.
So, it is always True.
(ii) Let the three consecutive even numbers be 2n, 2n + 2, 2n + 4
Sum = 2n + (2n + 2) + (2n + 4) = 6n + 6 = 6(n + 1)
This is 6 times a whole number, so it is always divisible by 6.
So, it is always True.
(iii) A number is a multiple of 6 if:
It is divisible by 2 (last digit even) and
It is divisible by 3 (sum of digits divisible by 3).
In abcdef and badcef:
• have the same digits, just rearranged, so their digit sum is the same → both are divisible by 3 or both are not.
• the last digit in both is ‘f’, so either both are even or both are odd.
So if abcdef is divisible by 2 and 3, then badcef is also divisible by 2 and 3.
Therefore, it is always True.
(iv) Simplifying the expression:
8(7b – 3) – 4(11b + 1) = 56b – 24 – 44b – 4
= (56b – 44b) + (–24 – 4) = 12b – 28
= 4(3b – 7)
For this to be a multiple of 12, 4(3b – 7) must have a factor 12.
We already have a factor 4, so (3b – 7) would need to be a multiple of 3.
But: 3b – 7 = 3(b – 3) + 2
This always leaves remainder 2 when divided by 3, so it is never a multiple of 3 for any whole number b. Also, 12b – 28 = 0 would give b = 28/12, not a whole number.
So the expression is never a multiple of 12.
Therefore, it is never True.

13. Choose any 3 numbers. When is their sum divisible by 3? Explore all possible cases and generalise.
See AnswerEvery number, when divided by 3, gives one of these:
► Remainder 0 → multiple of 3 (like 3, 6, 9, 12…)
► Remainder 1 → of the form 3k + 1 (like 1, 4, 7, 10…)
► Remainder 2 → of the form 3k + 2 (like 2, 5, 8, 11…)
So each of our 3 numbers is either:
► “type 0” (remainder 0),
► “type 1” (remainder 1), or
► “type 2” (remainder 2).
Let’s denote the types of the three numbers by (R1, R2, R3), where each R is 0, 1 or 2.
We check when the sum of remainders is 0 or a multiple of 3 (because then the whole sum is divisible by 3).
Possible useful cases:
1) All three are type 0: R1 = 0, R2 = 0, R3 = 0
Sum of remainders = 0 + 0 + 0 = 0 → divisible by 3
Example: 6, 12, 9 → all multiples of 3
Sum = 6 + 12 + 9 = 27 → divisible by 3
2) All three are type 1: R1 = 1, R2 = 1, R3 = 1
Sum of remainders = 1 + 1 + 1 = 3 → divisible by 3
Example: 4, 7, 10 → each leaves remainder 1 when divided by 3
Sum = 4 + 7 + 10 = 21 → divisible by 3
3) All three are type 2: R1 = 2, R2 = 2, R3 = 2
Sum of remainders = 2 + 2 + 2 = 6 → divisible by 3
Example:
5, 8, 11 → each leaves remainder 2 when divided by 3
Sum = 5 + 8 + 11 = 24 → divisible by 3
4) One of each type: 0, 1, 2
R1 = 0, R2 = 1, R3 = 2 (in any order)
Sum of remainders = 0 + 1 + 2 = 3 → divisible by 3
Example:
6 (remainder 0), 7 (remainder 1), 8 (remainder 2)
Sum = 6 + 7 + 8 = 21 → divisible by 3
Some cases that do NOT work:
5) Two of type 0 and one of type 1: 0 + 0 + 1 = 1 (not a multiple of 3)
Example: 6, 9, 4 → sum = 19 → not divisible by 3
6) Two of type 1 and one of type 2: 1 + 1 + 2 = 4 (not a multiple of 3)
Example: 4, 7, 5 → sum = 16 → not divisible by 3
7) Two of type 2 and one of type 1: 2 + 2 + 1 = 5 (not a multiple of 3)
Example: 5, 8, 4 → sum = 17 → not divisible by 3
The sum of three numbers is divisible by 3 exactly in these situations:
1) All three numbers give the same remainder when divided by 3:
– either all are multiples of 3, or
– all leave remainder 1, or
– all leave remainder 2.
2) The three numbers’ remainders are 0, 1, and 2 in some order.
In short: The sum of three numbers is divisible by 3 if their remainders (on division by 3) add up to 0, 3 or 6.

14. Is the product of two consecutive integers always multiple of 2? Why? What about the product of these consecutive integers? Is it always a multiple of 6? Why or why not? What can you say about the product of 4 consecutive integers? What about the product of five consecutive integers?
See Answer► Product of two consecutive integers and 2
Take two consecutive numbers: n and n+1. One of them is always even.
So their product n(n+1) always has a factor 2.
So, always a multiple of 2.
► Product of two consecutive integers and 6
To be a multiple of 6, the product must have factors 2 and 3.
It always has a 2 (as shown above). But it does not always have a 3.
Example: 4 × 5 = 20 (not a multiple of 6).
So, sometimes a multiple of 6, not always.
► Product of four consecutive integers
Take n, n+1, n+2, n+3.
Among these:
– there are two even numbers,
– one of them is a multiple of 4,
– and one number is a multiple of 3.
So the product always has factors 4, 2 and 3 → total factor 24.
So, always a multiple of 24.
► Product of five consecutive integers
Take n, n+1, n+2, n+3, n+4.
Among these:
– one is a multiple of 5,
– one is a multiple of 3,
– two or three are even and one of them is a multiple of 4.
So the product has factors 5, 3, 4 and at least one more 2.
This gives a factor of 120.
So, always a multiple of 120.

15. Solve the cryptarithms —
(i) EF × E = GGG
See AnswerWriting EF as 10E + F, then (10E + F) × E = 111G
We can try possible digits for E (from 1 to 9) and look for a neat triple digit.
Trying E = 3: EF could be 37:
37 × 3 = 111 → all digits 1
So, E = 3, F = 7, G = 1
Therefore, the answer is 37 × 3 = 111.

(ii) WOW × 5 = MEOW
See AnswerWriting WOW as a 3-digit number: W O W
MEOW is a 4-digit number: M E O W
► at the units place: W × 5 must end with W again.
The only digit with this property (0–9) is 5: 5 × 5 = 25 → ends with 5
So W = 5.
► Tens place.
We already know W = 5.
Units: 5 × 5 = 25 → write 5, carry 2.
Now 5 × O + 2 must end with O.
So, 5O + 2 ends with O
Trying O = 7: 5 × 7 + 2 = 35 + 2 = 37 → ends with 7.
So, O = 7, and we carry 3 to the next place.
► Hundreds place.
We have W = 5, carry = 3.
5 × W + 3 = 5 × 5 + 3 = 25 + 3 = 28
So we write 8 and carry 2.
Thus E = 8.
► Thousands place.
Only the carry 2 remains, so M = 2.
So, W = 5, O = 7, E = 8, M = 2
Therefore, WOW = 575 and MEOW = 2875.

16. Which of the following Venn diagrams captures the relationship between the multiples of 4, 8, and 32?

Answer: