NCERT Solutions for Class 8 Maths Ganita Prakash Chapter 6 We Distribute, Yet Things Multiply

Page 136

Consider the multiplication of two numbers, say, 23 × 27.
1. By how much does the product increase if the first number (23) is increased by 1?
2. What if the second number (27) is increased by 1?
3. How about when both numbers are increased by 1?
Do you see a pattern that could help generalise our observations to the product of any two numbers?
See Answer1. If the first number 23 is increased by 1, the new multiplication becomes 24 × 27.
According to the distributive property, (a + 1)b = ab + b.
So the product increases by 27.
2. If the second number 27 is increased by 1, the new multiplication becomes 23 × 28.
Using a(b + 1) = ab + a, the product increases by 23.
3. If both numbers are increased by 1, the new multiplication becomes 24 × 28.
Using the identity (a + 1)(b + 1) = ab + a + b + 1,
the product increases by 23 + 27 + 1 = 51.
Pattern:
If one number increases by 1, the product increases by the other number.
If both numbers increase by 1, the increase is a + b + 1.

Page 138

How do we expand this (a + 1) (b + 1)?
See AnswerExpansion:
(a + 1) (b + 1)
= ab + a + b + 1

What would we get if we had expanded (a + 1) (b + 1) by first taking (b + 1) as a single term? Try it?
See AnswerExpansion:
(a + 1) (b + 1)
= a(b + 1) + 1(b + 1)

What happens when one of the numbers in a product is increased by 1 and the other is decreased by 1? Will there be any change in the product?
See AnswerLet the two numbers be a and b.
Product = ab
If a is increased by 1 and b is decreased by 1, then their product
= (a + 1)(b – 1)
= ab – a + b – 1
So the change in the product is increase = b – a – 1
This means the product does not always increase.
It depends on the values of a and b.
• If b – a – 1 is positive, the product increases.
• If b – a – 1 is zero, the product stays the same.
• If b – a – 1 is negative, the product decreases.

Will the product always increase? Find 3 examples where the product decreases.
See AnswerNo, the product will not always increase.
From the product: (a + 1)(b – 1) = ab + b – a – 1
The change in the product is b – a – 1
If this value is negative, the product decreases. Below are 3 examples where the product decreases.
Example 1: a = 10 and b = 8
Change = b – a – 1 = 8 – 10 – 1 = –3
Negative → product decreases.
Original product = 10 × 8 = 80
New product = 11 × 7 = 77
It decreased.
Example 2: a = 15 and b = 12
Change = 12 – 15 – 1 = –4
Negative → product decreases.
Original product = 15 × 12 = 180
New product = 16 × 11 = 176
It decreased.
Example 3: a = 7 and b = 5
Change = 5 – 7 – 1 = –3
Negative → product decreases.
Original product = 7 × 5 = 35
New product = 8 × 4 = 32
It decreased.

What happens when a and b are negative integers?
See AnswerWhen a and b are negative integers, the same thing happens as with positive numbers.
It is given that the distributive property works for all integers. So the identity (a + 1)(b – 1) = ab + b – a – 1 also works when a and b are negative.
We just have to substitute the negative values and follow the same steps. The product may increase or decrease depending on the value of b – a – 1.
For example:
If a = –4 and b = –5, we can put these values and see what happens. The rule still works because negative numbers also follow the distributive property.
So, even for negative integers, the method does not change.

Page 139

By how much will the product of two numbers change if one of the numbers is increased by m and the other by n?
See AnswerIf one number is increased by m and the other by n, the new product becomes:
(a + m)(b + n)
Expanding this, we get: (a + m)(b + n) = ab + mb + an + mn
So the increase in the product is an + bm + mn.
This tells us how much the product changes when the first number goes up by m and the second number goes up by n.
This rule works for all integers.

Page 140

This identity can be used to find how products change when the numbers being multiplied are increased or decreased by any amount. Can you see how this identity can be used when one or both numbers are decreased?
See AnswerYes, we can use the same identity even when one or both numbers are decreased.
The identity is (a + m)(b + n) = ab + mb + an + mn
Here, m and n can be positive or negative.
So if a number is decreased, we simply take m or n as a negative number.
For example:
If a is increased by 1 and b is decreased by 1, then we take m = 1 and n = –1.
Putting these into the identity: (a + 1)(b – 1)
= ab + b – a – 1
So the identity works for increases and decreases, because decreases are written as adding a negative number.

Use Identity 1 to find how the product changes when
(i) one number is decreased by 2 and the other increased by 3;
(ii) both numbers are decreased, one by 3 and the other by 4.
See AnswerIdentity 1: (a + m)(b + n) = ab + mb + an + mn
The change in the product is mb + an + mn
(i) One number is decreased by 2 and the other is increased by 3
Decreased by 2 → m = –2
Increased by 3 → n = 3
Now substitute m = –2 and n = 3 in the identity change formula:
Change = mb + an + mn
= (–2)b + 3a + (–2 × 3)
= –2b + 3a – 6
So the product changes by 3a – 2b – 6.
(ii) Both numbers are decreased, one by 3 and the other by 4
First number decreased by 3 → m = –3
Second number decreased by 4 → n = –4
Change = mb + an + mn
= (–3)b + (–4)a + (–3 × –4)
= –3b – 4a + 12
So the product changes by 12 – 4a – 3b.

Verify the answers by finding the products without converting the subtractions to additions.
See AnswerVerification by direct products (without converting subtractions to additions)
We already found:
(i) Change = 3a – 2b – 6
(ii) Change = 12 – 4a – 3b
Now we verify each by multiplying directly.
(i) One number decreased by 2 and the other increased by 3
Original product: a × b = ab
New numbers: (a – 2) and (b + 3)
New product: (a – 2)(b + 3)
Now expand directly: (a – 2)(b + 3)
= a·b + a·3 – 2·b – 2·3
= ab + 3a – 2b – 6
Change in product = (new product – old product)
= (ab + 3a – 2b – 6) – ab
= 3a – 2b – 6
Hence Verified.
(ii) Both numbers decreased
First decreased by 3 → (a – 3)
Second decreased by 4 → (b – 4)
Original product: ab
New product: (a – 3)(b – 4)
Expand directly: (a – 3)(b – 4)
= a·b – 4a – 3b + 12
= ab – 4a – 3b + 12
Change in product = (new product – old product)
= (ab – 4a – 3b + 12) – ab
= 12 – 4a – 3b
Hence Verified.

Expand (i) (a – u) (b + v), (ii) (a – u) (b – v).
See Answer(i) Using distributive property:
(a – u)(b + v)
= a·b + a·v – u·b – u·v
= ab + av – ub – uv
(ii) Using distributive property:
(a – u)(b – v)
= a·b – a·v – u·b + u·v
= ab – av – ub + uv

Example 1: Expand 3a/2 (a – b + 1/5).
See Answer3a/2 (a – b + 1/5)
= (3a/2) × a – (3a/2) × b + (3a/2) × (1/5)
= 3/2 a² – 3/2 ab + 3/10 a

Page 141

Can any two terms be added to get a single term?
See AnswerNo, we cannot add any two terms to make a single term.
The terms we got were:
► 3/2 a²
► – 3/2 ab
► 3/10 a
All three terms have different letter parts:
• a²
• ab
• a
Since their letters are not the same, they are not like terms. Only like terms can be added.

Example 2: Expand (a + b) (a + b).
See AnswerFirst, distribute each term: (a + b)(a + b)
= a × a + b × a + a × b + b × b
= a² + ba + ab + b²
Now, ba and ab are like terms (both mean ab), so we add them: ba + ab = 2ab
So the final answer is a² + 2ab + b².

Example 3: Expand (a + b)(a² + 2ab + b²).
See AnswerDistributing (a + b) to each term inside the bracket: (a + b)(a² + 2ab + b²)
= (a + b)a² + (a + b)2ab + (a + b)b²
Now expanding each part:
• (a + b)a² = a·a² + b·a² = a³ + a²b
• (a + b)2ab = 2ab·a + 2ab·b = 2a²b + 2ab²
• (a + b)b² = a·b² + b·b² = ab² + b³
Now put all terms together: a³ + a²b + 2a²b + 2ab² + ab² + b³
Combine like terms:
a²b + 2a²b = 3a²b
ab² + 2ab² = 3ab²
So the final answer is a³ + 3a²b + 3ab² + b³.

Page 142

1. Observe the multiplication grid below. Each number inside the grid is formed by multiplying two numbers. If the middle number of a 3 × 3 frame is given by the expression pq, as shown in the figure, write the expressions for the other numbers in the grid.

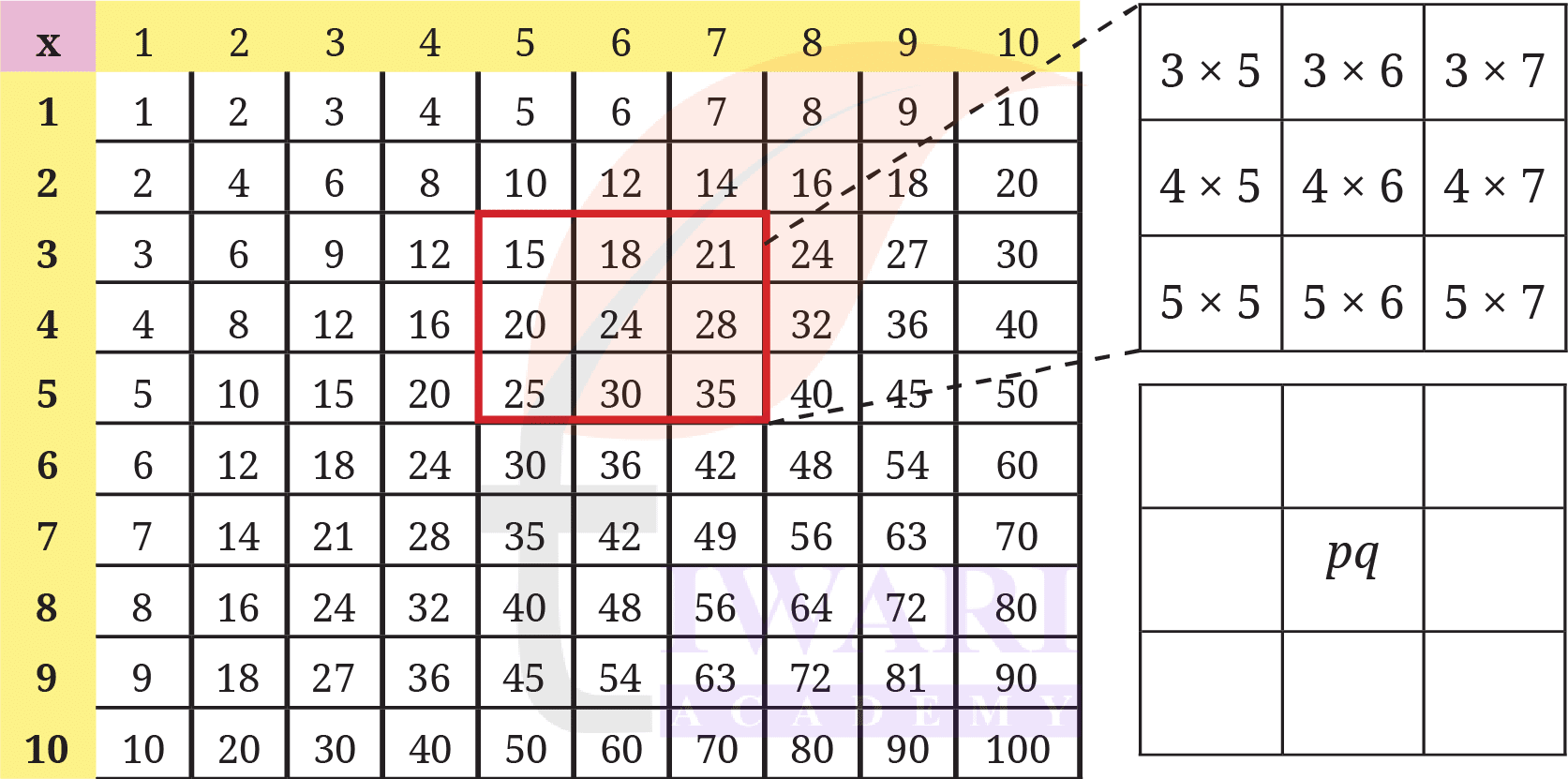
Answer:

2. Expand the following products.
(i) (3 + u) (v – 3)
(ii) 2/3(15 + 6a)
(iii) (10a + b) (10c + d)
(iv) (3 – x) (x – 6)
(v) (–5a + b) (c + d)
(vi) (5 + z) (y + 9)
See Answer(i) (3 + u)(v – 3)
= 3v – 9 + uv – 3u
= 3v + uv – 9 – 3u
(ii) 2/3 (15 + 6a)
2/3 × 15 = 10
2/3 × 6a = 4a
So, 2/3 (15 + 6a) = 10 + 4a
(iii) (10a + b)(10c + d)
(10a)(10c) = 100ac
(10a)(d) = 10ad
(b)(10c) = 10bc
(b)(d) = bd
So, (10a + b)(10c + d) = 100ac + 10ad + 10bc + bd
(iv) (3 – x)(x – 6)
(3)(x) = 3x
(3)(–6) = –18
(–x)(x) = –x²
(–x)(–6) = +6x
So, (3 – x)(x – 6) = 3x – 18 – x² + 6x
= –x² + 9x – 18
(v) (–5a + b)(c + d)
(–5a)(c) = –5ac
(–5a)(d) = –5ad
(b)(c) = bc
(b)(d) = bd
So, (–5a + b)(c + d) = –5ac – 5ad + bc + bd
(vi) (5 + z)(y + 9)
(5)(y) = 5y
(5)(9) = 45
(z)(y) = zy
(z)(9) = 9z
So, (5 + z)(y + 9) = 5y + 45 + zy + 9z

3. Find 3 examples where the product of two numbers remains unchanged when one of them is increased by 2 and the other is decreased by 4.
See AnswerWe want the product to remain the same when:
• one number is increased by 2, and
• the other is decreased by 4.
So if the original product is a × b
The new product becomes: (a + 2)(b – 4)
For the product to stay unchanged: (a + 2)(b – 4) = ab
⇒ ab – 4a + 2b – 8 = ab
⇒ –4a + 2b – 8 = 0
⇒ 2b – 4a – 8 = 0
⇒ b – 2a – 4 = 0
So, b = 2a + 4
This means any pair of numbers (a, b) that satisfy b = 2a + 4 will keep the product unchanged.
► Example 1
Let a = 1
Then b = 2(1) + 4 = 6
Original product: 1 × 6 = 6
New product: (1 + 2)(6 – 4) = 3 × 2 = 6
Product unchanged.
► Example 2
Let a = 2
Then b = 2(2) + 4 = 8
Original product: 2 × 8 = 16
New product: (2 + 2)(8 – 4) = 4 × 4 = 16
Product unchanged.
► Example 3
Let a = 3
Then b = 2(3) + 4 = 10
Original product: 3 × 10 = 30
New product: (3 + 2)(10 – 4) = 5 × 6 = 30
Product unchanged.

4. Expand (i) (a + ab – 3b²) (4 + b), and (ii) (4y + 7) (y + 11z – 3).
See Answer(i) Using distributive property
(a + ab – 3b²)(4 + b)
= (a + ab – 3b²) × 4 + (a + ab – 3b²) × b
= (4a + 4ab – 12b²) + (ab + ab² – 3b³)
= 4a + 5ab + ab² – 12b² – 3b³
(ii) Using distributive property
(4y + 7)(y + 11z – 3)
= 4y(y + 11z – 3) + 7(y + 11z – 3)
= (4y² + 44yz – 12y) + (7y + 77z – 21)
= 4y² + 44yz – 5y + 77z – 21

5. Expand (i) (a – b) (a + b), (ii) (a – b) (a² + ab + b²) and (iii) (a – b)(a³ + a²b + ab² + b³), Do you see a pattern? What would be the next identity in the pattern that you see? Can you check it by expanding?
See Answer(i) Using distributive property:
(a – b)(a + b)
= a² – b²
(ii) Using distributive property:
(a – b)(a² + ab + b²)
= a³ + a²b + ab² – (a²b + ab² + b³)
= a³ – b³
(iii) Using distributive property:
(a – b)(a³ + a²b + ab² + b³)
= a⁴ + a³b + a²b² + ab³ – (a³b + a²b² + ab³ + b⁴)
= a⁴ – b⁴
Yes there is a pattern. Every time we multiply:
(a – b) × (sum of all mixed powers of a and b)
we get: aⁿ – bⁿ
For n = 2 → a² – b²
For n = 3 → a³ – b³
For n = 4 → a⁴ – b⁴
The next identity will be:
(a – b)(a⁴ + a³b + a²b² + ab³ + b⁴)
= a⁵ – b⁵
Checking by expanding:
(a – b)(a⁴ + a³b + a²b² + ab³ + b⁴)
= a⁵ + a⁴b + a³b² + a²b³ + ab⁴ – (a⁴b + a³b² + a²b³ + ab⁴ + b⁵)
= a⁵ – b⁵
The pattern is correct.

Use the following multiplications to find the product of a number with 11 in a single step. (a) 3874 × 11 (b) 5678 × 11
See Answer(a) 3874 × 11
Writing the number with space between digits: 3 8 7 4
Now insert sums:
• Between 3 and 8 → 3 + 8 = 11
• Between 8 and 7 → 8 + 7 = 15
• Between 7 and 4 → 7 + 4 = 11
Now write step by step with carries:
Start with last digit → 4
Next → 7 + 4 = 11 → write 1, carry 1
Next → 8 + 7 + carry (1) = 16 → write 6, carry 1
Next → 3 + 8 + carry (1) = 12 → write 2, carry 1
First digit + carry → 3 + carry (1) = 4
Final number: 42614
So, 3874 × 11 = 42614
(b) 5678 × 11
Digits: 5 6 7 8
Sums:
• 5 + 6 = 11
• 6 + 7 = 13
• 7 + 8 = 15
Now apply carries:
Last digit → 8
7 + 8 = 15 → write 5, carry 1
6 + 7 + 1 = 14 → write 4, carry 1
5 + 6 + 1 = 12 → write 2, carry 1
First digit + carry → 5 + 1 = 6
Final answer: 62458
So, 5678 × 11 = 62458

Page 144

Describe a general rule to multiply a number (of any number of digits) by 11 and write the product in one line.
Evaluate (i) 94 × 11, (ii) 495 × 11, (iii) 3279 × 11, (iv) 4791256 × 11.
See AnswerTo multiply any number by 11 in one line:
► Write the first digit.
► Add each pair of neighbouring digits and write the sums in order.
► Write the last digit.
► If any sum is 10 or more, carry over the extra digit.
(i) 94 × 11
Digits: 9 4
Sum: 9 + 4 = 13
Write with carries:
• Last digit → 4
• Middle → 13 → write 3, carry 1
• First digit + carry → 9 + 1 = 10
So, 94 × 11 = 1034
(ii) 495 × 11
Digits: 4 9 5
Sums: 4 + 9 = 13, 9 + 5 = 14
Write with carries:
• Last digit → 5
• 9 + 5 = 14 → write 4, carry 1
• 4 + 9 + 1 = 14 → write 4, carry 1
• First digit + carry → 4 + 1 = 5
So, 495 × 11 = 5445
(iii) 3279 × 11
Digits: 3 2 7 9
Sums:
3 + 2 = 5
2 + 7 = 9
7 + 9 = 16
Now write:
• Last digit → 9
• 7 + 9 = 16 → write 6, carry 1
• 2 + 7 + 1 = 10 → write 0, carry 1
• 3 + 2 + 1 = 6
• First digit → 3
So, 3279 × 11 = 36069
(iv) 4791256 × 11
Digits: 4 7 9 1 2 5 6
Sums:
4 + 7 = 11
7 + 9 = 16
9 + 1 = 10
1 + 2 = 3
2 + 5 = 7
5 + 6 = 11
Now place digits and carry:
• Last digit → 6
• 5 + 6 = 11 → write 1, carry 1
• 2 + 5 + 1 = 8
• 1 + 2 = 3
• 9 + 1 = 10 → write 0, carry 1
• 7 + 9 + 1 = 17 → write 7, carry 1
• 4 + 7 + 1 = 12 → write 2, carry 1
• First digit + carry → 4 + 1 = 5
So, 4791256 × 11 = 52703716

Can we come up with a similar rule for multiplying a number by 101?
Multiply 3874 by 101.
Use this to multiply 3874 × 101 in one line.
See Answer► Yes, we can make a similar rule for multiplying a number by 101.
It is given that: number × 101 = number × (100 + 1)
So, to multiply any number by 101:
Write the number with two zeros added to the right.
Write the same number below it.
Add the two numbers.
This gives the product in one step.
► Multiplication of 3874 by 101 = 3874 × 101 = 391274
► Multiplication of 3874 × 101 in one line:
3874 × 101 = 387400 + 3874 = 391274
This method works for any number.

What could be a general rule to multiply a number by 101 and write the product in one line? Extend this rule for multiplication by 1001, 10001, …
See AnswerA general rule to multiply any number by 101 is:
► Write the number.
► Write the same number again, but shifted two places to the right (like adding two zeros).
► Add the two numbers.
This gives the product in one line.
Example:
3874 × 101 = 387400 + 3874 = 391274
This idea can be extended: For × 1001:
► Write the number.
► Write the same number again, shifted three places to the right.
► Add them.
For × 10001:
► Write the number.
► Write the same number again, shifted four places to the right.
► Add them.
So for multiplication by 101, 1001, 10001, …
just write the number twice and the second copy is shifted according to the number of zeros.

Use this to find (i) 89 × 101, (ii) 949 × 101, (iii) 265831 × 1001, (iv) 1111 × 1001, (v) 9734 × 99 and (vi) 23478 × 999.
See Answer(i) 89 × 101
Using the rule: number × 101 = number with two zeros + number
So, 89 × 101
= 8900 + 89
= 8989
(ii) 949 × 101
= 94900 + 949
= 95849
(iii) 265831 × 1001
Using the Rule: number × 1001 = number with three zeros + number
265831 × 1001
= 265831000 + 265831
= 266096831
(iv) 1111 × 1001
= 1111000 + 1111
= 1112111
(v) 9734 × 99
We know that: 99 = 100 – 1
So use distributive property:
9734 × 99
= 9734 × (100 – 1)
= 973400 – 9734
= 963666
(vi) 23478 × 999
Putting 999 = 1000 – 1, we have
23478 × 999
= 23478 × (1000 – 1)
= 23478000 – 23478
= 23454522

Page 145

The area of a square of sidelength 60 units is 3600 sq. units (60²) and that of a square of sidelength 5 units is 25 sq. units (5²). Can we use this to find the area of a square of sidelength 65 units?
See AnswerYes, we can use the areas of 60² and 5² to find the area of a square of side 65.
Since 65 = 60 + 5
We can split the big square into:
• one square of side 60
• one square of side 5
• two rectangles of sides 60 and 5
So the area is: (60 + 5)²
= 60² + 5² + 2 × 60 × 5
= 3600 + 25 + 600
= 4225 sq. units
So, the area of the square with sidelength 65 is 4225 square units.

What if we write 65² as (30 + 35)² or (52 + 13)²?
See AnswerIf we write 65² as (30 + 35)² or (52 + 13)², we will still get the same area because all these pairs add up to 65.
Using the formula: (a + b)² = a² + b² + 2ab
► For (30 + 35)²:
(30 + 35)²
= 30² + 35² + 2 × 30 × 35
= 900 + 1225 + 2100
= 4225
► For (52 + 13)²:
(52 + 13)²
= 52² + 13² + 2 × 52 × 13
= 2704 + 169 + 1352
= 4225
So, no matter how we split 65, 65² = 4225 sq. units.

If a and b are any two integers, is (a + b)² always greater than a² + b²? If not, when is it greater?
See Answer(a + b)² is not always greater than a² + b².
We know that: (a + b)² = a² + b² + 2ab
So, the difference between them is: (a + b)² – (a² + b²) = 2ab
This means:
• If 2ab > 0, then (a + b)² is greater.
• If 2ab = 0, then they are equal.
• If 2ab < 0, then (a + b)² is smaller. Now, when is 2ab > 0?
When a and b have the same sign (both positive or both negative).
So, (a + b)² is greater than a² + b² when a and b are either both positive or both negative.
If one is positive and the other is negative, the product ab becomes negative and the result is not greater.

Use Identity 1A to find the values of 104², 37². (Hint: Decompose 104 and 37 into sums or differences of numbers whose squares are easy to compute.)
See AnswerIdentity 1A: (a + b)² = a² + b² + 2ab
We must break the numbers into easy parts.
► 104²
104 can be written as: 104 = 100 + 4
Now apply Identity 1A: (100 + 4)²
= 100² + 4² + 2 × 100 × 4
= 10000 + 16 + 800
= 10816
So, 104² = 10816
► 37²
37 can be written as: 37 = 40 + (– 3)
Now apply Identity 1A: [40 + (– 3)]²
= 40² + (-3)² + 2 × 40 ×(- 3)
= 1600 + 9 – 240
= 1369
So, 37² = 1369

Page 146

Use Identity 1A to write the expressions for the following.
(i) (m + 3)²
(ii) (6 + p)²
See Answer(i) (m + 3)²
Using Identity 1A: (m + 3)²
= m² + 3² + 2·m·3
= m² + 9 + 6m
= m² + 6m + 9
(ii) (6 + p)²
Using Identity 1A: (6 + p)²
= 6² + p² + 2·6·p
= 36 + p² + 12p
= p² + 12p + 36

Expand (6x + 5)².
See AnswerWe use Identity 1A: (a + b)² = a² + b² + 2ab
Here,
a = 6x
b = 5
So, (6x + 5)²
= (6x)² + 5² + 2·(6x)·5
= 36x² + 25 + 60x
= 36x² + 60x + 25

Expand (3j + 2k)² using both the identity and by applying the distributive property.
See AnswerIdentity 1A: (a + b)² = a² + b² + 2ab
Here,
a = 3j
b = 2k
So, (3j + 2k)²
= (3j)² + (2k)² + 2·(3j)(2k)
= 9j² + 4k² + 12jk
= 9j² + 12jk + 4k²
Using Distributive Property:
(3j + 2k)(3j + 2k)
= 3j(3j + 2k) + 2k(3j + 2k)
= (9j² + 6jk) + (6jk + 4k²)
= 9j² + 12jk + 4k²

Can we use 60² (=3600) and 5² (=25) to find the value of (60 – 5)² or 55²?
See AnswerYes, we can use 60² and 5² to find the value of (60 – 5)² or 55².
We write: 55 = 60 – 5
Now use the identity for (a – b)²: (a – b)² = a² + b² – 2ab
So, (60 – 5)²
= 60² + 5² – 2 × 60 × 5
= 3600 + 25 – 600
= 3025
So, 55² = 3025

Page 147

We can also use the expansion of (a + b)² to find the expansion of (a – b)². Think how.
See AnswerYes, we can use the expansion of (a + b)² to get the expansion of (a – b)².
The idea is: (a – b)² can be written as (a + (–b))²
Now apply the formula for (a + b)²: (a + b)² = a² + b² + 2ab
Here b is replaced by (–b):
(a + (–b))²
= a² + (–b)² + 2·a·(–b)
= a² + b² – 2ab
So, (a – b)² = a² + b² – 2ab
This is the expansion of (a – b)², obtained directly from (a + b)².

Find the general expansion of (a – b)² using geometry, as we did for 55².
See AnswerTo get the general expansion of (a – b)² using geometry, we imagine a big square of side a and remove two rectangles of side a and b, just like we did for 60 and 5.
Start with a square of side a: Area = a²
Inside it, imagine a smaller square of side b in one corner.
When we remove the two rectangles of size a × b, we have removed the small b × b square twice. So we add it back once.
So the area becomes: a² – ab – ab + b² = a² – 2ab + b²
Final geometric expansion: (a – b)² = a² – 2ab + b²
This is the same idea used for 55².

Use the identity (a – b)² to find the values of (a) 99² and (b) 58².
See AnswerIdentity: (a – b)² = a² + b² – 2ab
► 99²
99 can be written as: 99 = 100 – 1
Now applying the identity: (100 – 1)²
= 100² + 1² – 2 × 100 × 1
= 10000 + 1 – 200
= 9801
So, 99² = 9801
► 58²
58 can be written as: 58 = 60 – 2
Now applying the identity: (60 – 2)²
= 60² + 2² – 2 × 60 × 2
= 3600 + 4 – 240
= 3364
So, 58² = 3364

Expand the following using both Identity 1B and by applying the distributive property
(i) (b – 6)²
(ii) (–2a + 3)²
(iii) (7y – 3/4z)²
See AnswerIdentity 1B: (a – b)² = a² – 2ab + b²
(i) (b – 6)²
Using Identity 1B
Here a = b, b = 6:
(b – 6)²
= b² – 2·b·6 + 6²
= b² – 12b + 36
Using Distributive Property
(b – 6)(b – 6)
= b·b – 6·b – 6·b + 36
= b² – 12b + 36
(ii) (–2a + 3)²
Rewrite it as: (3 – 2a)²
Using Identity 1B: (a – b)² = a² – 2ab + b²
Here: a = 3, b = 2a
(3 – 2a)²
= 3² – 2·3·(2a) + (2a)²
= 9 – 12a + 4a²
Using Distributive Property
(3 – 2a)(3 – 2a)
= 3·3 – 6a – 6a + 4a²
= 9 – 12a + 4a²
(iii) (7y – 3/4 z)²
Let a = 7y, b = 3/4 z
Using Identity 1B
(7y – 3/4 z)²
= (7y)² – 2·(7y)(3/4 z) + (3/4 z)²
= 49y² – (21/2)yz + 9/16 z²
Using Distributive Property
(7y – 3/4 z)(7y – 3/4 z)
= 49y² – (21/2)yz – (21/2)yz + 9/16 z²
= 49y² – (21/2)yz + 9/16 z²

Page 148

Take a pair of natural numbers. Calculate the sum of their squares. Can you write twice this sum as a sum of two squares?
See AnswerLet any pair of natural numbers be a and b.
First calculate the sum of their squares: a² + b²
Now take twice this sum: 2(a² + b²)
Now, (a + b)² + (a – b)²
= (a² + 2ab + b²) + (a² – 2ab + b²)
= 2a² + 2b²
= 2(a² + b²)
So, 2(a² + b²) = (a + b)² + (a – b)²
This means twice the sum of squares can always be written as the sum of two squares.
Example: Take the numbers 5 and 6.
Sum of their squares: 5² + 6² = 25 + 36 = 61
Twice this sum: 2 × 61 = 122
Now write it as sum of two squares:
(5 + 6)² + (5 – 6)²
= 11² + (–1)²
= 121 + 1
= 122

Do the identities below help in explaining the observed pattern?
(a + b)² = a² + 2ab + b²
(a – b)² = a² – 2ab + b²
See AnswerYes, these identities help explain the pattern.
We have:
(a + b)² = a² + 2ab + b²
(a – b)² = a² – 2ab + b²
Now add both identities: (a + b)² + (a – b)²
= (a² + 2ab + b²) + (a² – 2ab + b²)
The terms +2ab and –2ab cancel out. So we get:
= a² + a² + b² + b²
= 2a² + 2b²
= 2(a² + b²)
This shows exactly why: 2(a² + b²) = (a + b)² + (a – b)²
So the pattern is explained by these identities.

Here is a related pattern. Try to describe the pattern using algebra to determine if the pattern always holds.
9 × 9 – 1 × 1 = 10 × 8
8 × 8 – 6 × 6 = 14 × 2
7 × 7 – 2 × 2 = 9 × 5
10 × 10 – 4 × 4 = 14 × 6
See AnswerThe given pattern:
9 × 9 – 1 × 1 = 10 × 8
8 × 8 – 6 × 6 = 14 × 2
7 × 7 – 2 × 2 = 9 × 5
10 × 10 – 4 × 4 = 14 × 6
On the left side, we always have: a × a – b × b = a² – b²
On the right side, we have: (a + b)(a – b)
So the pattern is: a² – b² = (a + b)(a – b)
Now we check this using algebra (distributive property):
(a + b)(a – b)
= a·a – a·b + b·a – b·b
= a² – ab + ab – b²
= a² – b²
So the two sides are equal.
Therefore, the pattern a² – b² = (a + b)(a – b) always holds for any numbers a and b.

Use Identity 1C to calculate 98 × 102, and 45 × 55.
See AnswerIdentity 1C: (a + b)(a – b) = a² – b²
► 98 × 102
98 and 102 are equally spaced around 100.
So, 98 = 100 – 2
102 = 100 + 2
Now using Identity 1C:
(100 – 2)(100 + 2)
= 100² – 2²
= 10000 – 4
= 9996
So, 98 × 102 = 9996
► 45 × 55
Here the midpoint is 50:
45 = 50 – 5
55 = 50 + 5
Now use Identity 1C:
(50 – 5)(50 + 5)
= 50² – 5²
= 2500 – 25
= 2475
So, 45 × 55 = 2475

Show that (a + b) × (a – b) = a² – b² geometrically.

See AnswerTo show geometrically that (a + b)(a – b) = a² – b², we use a square picture.
Draw a big square of side a. Its area is a².
Inside it, remove a smaller square of side b from one corner. The area removed is b².
The remaining shape looks like a rectangle. Its length is a + b and its width is a – b.
When we remove the b × b square, one side becomes shorter by b and the other side becomes longer by b.
So the area of the remaining rectangle is: (a + b)(a – b)
But this area is also equal to: a² – b²
Since both represent the same area, we get (a + b)(a – b) = a² – b²
This shows the identity geometrically.

Page 149

Why is this identity true?
See AnswerThe identity (a + b)(a – b) = a² – b² is true because both sides represent the same area in two different ways.
Think of a big square of side a. Its area is a².
Inside it, take out a small square of side b. The area removed is b².
So the remaining area is a² – b², but this remaining shape can also be seen as a rectangle.
Its length becomes (a + b) and its width becomes (a – b).
So the area is also (a + b)(a – b).
Since both expressions describe the same region, their areas must be equal.
Therefore, (a + b)(a – b) = a² – b²
That is why the identity is true.

Page 149

1. Which is greater: (a – b)² or (b – a)²? Justify your answer.
See Answer(a – b)² and (b – a)² are always equal.
This is because when we square a number, the sign disappears.
For example, 5² = 25 and (–5)² = 25.
Here, b – a = –(a – b)
So, (b – a)² = [–(a – b)]²
= (a – b)²
Both are the same.
Therefore, neither is greater. (a – b)² = (b – a)² for all values of a and b.

2. Express 100 as the difference of two squares.
See AnswerWe have to write 100 as a difference of two squares.
100 = a² – b²
Now two numbers whose product is 100 using: a² – b² = (a + b)(a – b)
Taking the pair: 25 × 4 = 100
So, a + b = 25 and a – b = 4
Add the equations: 2a = 29 ⇒ a = 14.5 and b = 10.5
Now: a² – b² = 14.5² – 10.5²
= (210.25 – 110.25)
= 100
Therefore, 100 = 14.5² – 10.5²

3. Find 406², 72², 145², 1097² and 124² using the identities you have learnt so far.
See Answer► 406²
406 = 400 + 6
⇒ (400 + 6)²
= 400² + 6² + 2·400·6
= 160000 + 36 + 4800
= 164836
So, 406² = 164836
► 72²
72 = 70 + 2
⇒ (70 + 2)²
= 70² + 2² + 2·70·2
= 4900 + 4 + 280
= 5184
So, 72² = 5184
► 145²
145 = 150 – 5
⇒ (150 – 5)²
= 150² + 5² – 2·150·5
= 22500 + 25 – 1500
= 21025
So, 145² = 21025
► 1097²
1097 = 1100 – 3
⇒ (1100 – 3)²
= 1100² + 3² – 2·1100·3
= 1210000 + 9 – 6600
= 1203409
So, 1097² = 1203409
► 124²
124 = 120 + 4
⇒ (120 + 4)²
= 120² + 4² + 2·120·4
= 14400 + 16 + 960
= 15376
So, 124² = 15376

4. Do Patterns 1 and 2 hold only for counting numbers? Do they hold for negative integers as well? What about fractions? Justify your answer.
See AnswerPatterns 1 and 2 come from the identities:
(a + b)² = a² + b² + 2ab
(a – b)² = a² + b² – 2ab
(a + b)(a – b) = a² – b²
These identities do not depend on a and b being counting numbers only.
They work for:
• counting numbers (1, 2, 3, …)
• negative integers
• fractions
• all real numbers
Because the distributive property works for all numbers.
Taking Pattern 2: a² – b² = (a + b)(a – b)
Taking a = –5, b = 2:
Left side: (–5)² – 2² = 25 – 4 = 21
Right side: (–5 + 2)(–5 – 2) = (–3)(–7) = 21
Both sides match.
So the pattern works for negative integers too.
Now, taking a = 1/2 and b = 1/3:
Left side: (1/2)² – (1/3)² = 1/4 – 1/9 = 5/36
Right side: (1/2 + 1/3)(1/2 – 1/3) = (5/6)(1/6) = 5/36
Again both sides match.
Therefore, Patterns 1 and 2 hold for all numbers, not just counting numbers, because the algebraic identities behind them are true for every integer, fraction and real number.

Page 150

We have expanded and simplified some algebraic expressions below to their simplest forms.
(i) Check each of the simplifications and see if there is a mistake.
(ii) If there is a mistake, try to explain what could have gone wrong.
(iii) Then write the correct expression.

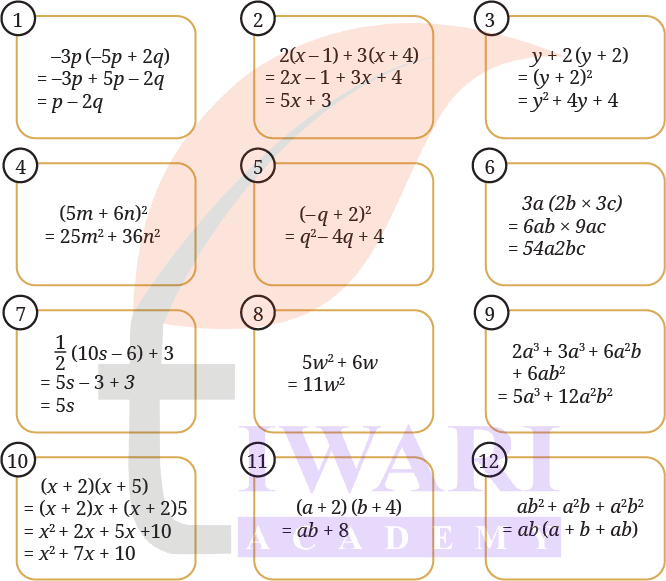
See Answer1. –3p (–5p + 2q)
Given: –3p + 5p – 2q = p – 2q
• Mistake: They did not multiply p with p and q.
• Correct: –3p(–5p + 2q) = 15p² – 6pq
2. 2(x – 1) + 3(x + 4)
Given: 2x – 1 + 3x + 4 = 5x + 3
• Mistake: 2 × (–1) should be –2, not –1; 3 × 4 should be 12, not 4.
• Correct: 2(x – 1) + 3(x + 4) = 2x – 2 + 3x + 12 = 5x + 10
3. y + 2(y + 2)
Given: (y + 2)² = y² + 4y + 4
• Mistake: y + 2(y + 2) is not (y + 2)².
• Correct: y + 2(y + 2) = y + 2y + 4 = 3y + 4
4. (5m + 6n)²
Given: 25m² + 36n²
• Mistake: Middle term 2 × 5m × 6n is missing.
• Correct: (5m + 6n)² = 25m² + 60mn + 36n²
5. (–q + 2)²
Given: q² – 4q + 4
• This is correct. No mistake.
6. 3a (2b × 3c)
Given: 6ab × 9ac = 54a²bc
• Mistake: They unnecessarily multiplied in two stages and changed the expression.
• Correct way:
2b × 3c = 6bc
3a × 6bc = 18abc
• Correct final answer: 18abc
7. 1/2 (10s – 6) + 3
Given: 5s – 3 + 3 = 5s
• This is correct. No mistake.
8. 5w² + 6w
Given: 11w²
• Mistake: w² and w are not like terms, so they cannot be added.
• Correct: Expression already in simplest form: 5w² + 6w
9. 2a³ + 3a³ + 6a²b + 6ab²
Given: 5a³ + 12a²b²
• Mistake: – 2a³ + 3a³ are like terms (OK),
– but 6a²b and 6ab² are not like terms and cannot be added to make 12a²b².
• Correct: 2a³ + 3a³ = 5a³
So final answer: 5a³ + 6a²b + 6ab²
10. (x + 2)(x + 5)
Given: (x + 2)x + (x + 2)5 = x² + 2x + 5x + 10 = x² + 7x + 10
• This is correct. No mistake.
11. (a + 2)(b + 4)
Given: ab + 8
• Mistake: Only ab and 2×4 are considered; other products are missing.
• Correct: (a + 2)(b + 4) = ab + 4a + 2b + 8
12. ab² + a²b + a²b²
Given: ab(a + b + ab)
• Take ab common:
ab² = ab·b
a²b = ab·a
a²b² = ab·ab
• So: ab² + a²b + a²b² = ab(b + a + ab)
And a + b = b + a, so their factorisation is fine.
• This is correct. No mistake.

Page 152

Use this formula to find the number of circles in Step 15.
See AnswerThe number of circles in Step k is given by the formula: k² + 2k
Finding the number of circles in Step 15, substitute k = 15:
15² + 2×15
= 225 + 30
= 255
Therefore, there are 255 circles in Step 15.

Consider the pattern made of square tiles in the picture below.

See AnswerThe pattern in made from the square tiles:3² – 1², 4² – 2², 5² – 3², …
That is (k + 2)² – k²
So, the number of tiles in step k: (k + 2)² – k²
= k² + 4k + 4 – k²
= 4k + 4

Page 153

How many square tiles are there in each figure?
See AnswerThe number of tiles in k step = 4k + 4
Therefore:
In figure 1, k = 1
So, tiles = 4 x 1 + 4 = 8
In figure 2, k = 2
So, tiles = 4 x 2 + 4 = 12
In figure 3, k = 3
So, tiles = 4 x 3 + 4 = 16

How many are there in Step 4 of the sequence? What about Step 10?
See AnswerIn step 4, k = 4
So, tiles = 4 x 4 + 4 = 20
In step 10, k = 10
So, tiles = 4 x 10 + 4 = 44

Write an algebraic expression for the number of tiles in Step n. Share your methods with the class. Can you find more than one method to arrive at the answer?
See AnswerThe number of tiles in step n: (n + 2)² – n²
= n² + 4n + 4 – n²
= 4n + 4

Find the area of the (interior) shaded region in the figure below. All four rectangles have the same dimensions.

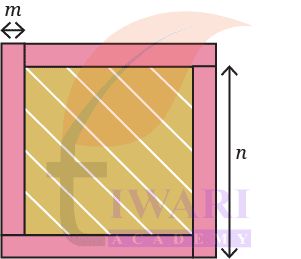
See AnswerLength of complete square region = n + m
So, the length of inner square region = n – m
Therefore, the area of inner square region = (n – m)².

By expanding both expressions,
check that (m + n)²– 4mn = (n – m)².
See AnswerLHS = (m + n)² – 4mn
= (m² + 2mn + n²) – 4mn
= m² + n² – 2mn
RHS (n – m)²
= n² – 2nm + m²
= m² + n² – 2mn
So, LHS = RHS
Therefore, (m + n)² – 4mn = (n – m)².

Find out the area of the region with slanting lines in the figure. All three rectangles have the same dimensions (Fig. 1).

See AnswerWe have to find the area of the region with slanting lines.
All three rectangles in the figure have the same dimensions x by y.
Area of ABCD = x².
Area of EFGH = xy.
Required area = Area (ABCD) – Area (EFGH) = x² – xy.

Page 154

By expanding the expressions, verify that all three expressions are equivalent. If x = 8 and y = 3, find the area of the shaded region.
See Answer► Expression 1: x² – xy
(This is already simplified.)
► Expression 2: x(x + 2y) – 3xy
= x² + 2xy – 3xy
= x² – xy
Matches Expression 1.
► Expression 3: x(x – y)
= x² – xy
Matches Expression 1 and 2.
Therefore, all three expressions are equivalent and represent the same area.
Substituting x = 8 and y = 3 in area = x² – xy, we get
Area = 8² – 8×3
= 64 – 24
= 40

Write an expression for the area of the dashed region in the figure below. Use more than one method to arrive at the answer. Substitute p = 6, r = 3.5, and s = 9, and calculate the area.

See Answer► Direct method
Length of dashed region = (p – r)
Width of dashed region = (s – r)
So area = (p – r)(s – r)
= ps – pr – rs + r²
► Rearranging the pieces
Area of dashed region = area of complete rectangle – (area of two rectangles with lenght p and s having width r) + common area of two rectangles
= ps – (pr + sr) + r²
= ps – pr – sr + r²
► Substituting p = 6, r = 3.5, s = 9
A = ps – pr – sr + r²
= 6×9 – 6×3.5 – 9×3.5 + (3.5)²
= 54 – 21.0 – 31.5 + 12.25
= 13.75

Page 154

1. Compute these products using the suggested identity.
(i) 46² using Identity 1A for (a + b)²
(ii) 397 × 403 using Identity 1C for (a + b) (a – b)
(iii) 91² using Identity 1B for (a – b)²
(iv) 43 × 45 using Identity 1C for (a + b) (a – b)
See Answer(i) 46² using Identity 1A: (a + b)² = a² + b² + 2ab
46 = 40 + 6
Therefore, (40 + 6)²
= 40² + 6² + 2·40·6
= 1600 + 36 + 480
= 2116
So, 46² = 2116
(ii) 397 × 403 using Identity 1C: (a + b)(a – b) = a² – b²
Middle value = 400
397 = 400 – 3
403 = 400 + 3
So, (400 – 3)(400 + 3)
= 400² – 3²
= 160000 – 9
= 159991
So, 397 × 403 = 159991
(iii) 91² using Identity 1B: (a – b)² = a² + b² – 2ab
91 = 100 – 9
Therefore, (100 – 9)²
= 100² + 9² – 2·100·9
= 10000 + 81 – 1800
= 8200 + 81 = 8281
So, 91² = 8281
(iv) 43 × 45 using Identity 1C: (a + b)(a – b) = a² – b²
Middle value = 44
43 = 44 – 1
45 = 44 + 1
Therefore, (44 – 1)(44 + 1)
= 44² – 1²
= 1936 – 1
= 1935
So, 43 × 45 = 1935

2. Use either a suitable identity or the distributive property to find each of the following products.
(i) (p – 1) (p + 11)
(ii) (3a – 9b) (3a + 9b)
(iii) –(2y + 5) (3y + 4)
(iv) (6x + 5y)²
(v) (2x – 1/2)²
(vi) (7p) × (3r) × (p + 2)
See Answer(i) (p – 1)(p + 11)
Using distributive property: (p – 1)(p + 11)
= p(p + 11) – 1(p + 11)
= (p² + 11p) – (p + 11)
= p² + 10p – 11
(ii) (3a – 9b)(3a + 9b)
This is of the form (A – B)(A + B) = A² – B².
A = 3a, B = 9b
Therefore, (3a – 9b)(3a + 9b)
= (3a)² – (9b)²
= 9a² – 81b²
(iii) –(2y + 5)(3y + 4)
First expanding, then putting the minus sign.
(2y + 5)(3y + 4)
= 2y·3y + 2y·4 + 5·3y + 5·4
= 6y² + 8y + 15y + 20
= 6y² + 23y + 20
Now put the minus sign:
–(6y² + 23y + 20)
= –6y² – 23y – 20
(iv) (6x + 5y)²
Using (a + b)² = a² + b² + 2ab
(6x + 5y)²
= (6x)² + (5y)² + 2·6x·5y
= 36x² + 25y² + 60xy
(v) (2x – 1/2)²
Using (a – b)² = a² + b² – 2ab
(2x – 1/2)²
= (2x)² + (1/2)² – 2·2x·(1/2)
= 4x² + 1/4 – 2x
(vi) (7p)(3r)(p + 2)
Multiplying the constants first: 7p × 3r = 21pr
So the expression becomes: 21pr(p + 2)
= 21pr·p + 21pr·2
= 21p²r + 42pr

3. For each statement identify the appropriate algebraic expression(s).
(i) Two more than a square number.

See Answers² + 2

(ii) The sum of the squares of two consecutive numbers.

See Answerm² + (m + 1)²

4. Consider any 2 by 2 square of numbers in a calendar, as shown in the figure.

Find products of numbers lying along each diagonal — 4 × 12 = 48, 5 × 11 = 55. Do this for the other 2 by 2 squares. What do you observe about the diagonal products? Explain why this happens.
See AnswerTaking a 2 by 2 square on the calendar.
Diagonal products:
7 × 15 = 105
8 × 14 = 112
So one diagonal product is 7 (112 – 105) more than the other.
If we try with other 2×2 squares, we will again get the same thing: the product on one diagonal is always 7 more than the product on the other diagonal.
If we label any 2×2 block like this:
top-left: a
top-right: a + 1
bottom-left: a + 7
bottom-right: a + 8
Diagonal 1: top-left × bottom-right = a(a + 8) = a² + 8a
Diagonal 2: top-right × bottom-left = (a + 1)(a + 7)
= a² + 7a + a + 7
= a² + 8a + 7
Difference = (a² + 8a + 7) – (a² + 8a) = 7
So the product along one diagonal is always 7 more than the product along the other diagonal, for every 2×2 square in the calendar.

5. Verify which of the following statements are true.
(i) (k + 1) (k + 2) – (k + 3) is always 2.
(ii) (2q + 1) (2q – 3) is a multiple of 4.
(iii) Squares of even numbers are multiples of 4, and squares of odd numbers are 1 more than multiples of 8.
(iv) (6n + 2)² – (4n + 3)² is 5 less than a square number.
See Answer(i) (k + 1)(k + 2) – (k + 3) is always 2
Now: (k + 1)(k + 2) = k² + 3k + 2
Now subtracting (k + 3): (k² + 3k + 2) – (k + 3) = k² + 2k – 1
This is not always equal to 2.
Example:
If k = 1 → 1 + 2 – 1 = 2 (true)
If k = 2 → 4 + 4 – 1 = 7 (not 2)
So, the statement (i) is false.
(ii) (2q + 1)(2q – 3) is a multiple of 4
Now: (2q + 1)(2q – 3)
= 4q² – 6q + 2q – 3
= 4q² – 4q – 3
This is 4(q² – q) – 3.
This is 3 less than a multiple of 4, not a multiple of 4.
So, the statement (ii) is false.
(iii) Let even number = 2m
(2m)² = 4m² → multiple of 4
Let odd number = 2m + 1
(2m + 1)² = 4m² + 4m + 1
= 4m(m + 1) + 1
Now m(m + 1) is always even, so: 4 × even = 8 × something
Thus the square is 8k + 1
So odd squares are 1 more than a multiple of 8.
So, the statement (iii) is true.
(iv) (6n + 2)² – (4n + 3)² is 5 less than a square number
Using identity 1C: A² – B² = (A + B)(A – B)
A = 6n + 2
B = 4n + 3
A + B = (6n + 2) + (4n + 3) = 10n + 5
A – B = (6n + 2) – (4n + 3) = 2n – 1
Difference: (6n + 2)² – (4n + 3)² = (10n + 5)(2n – 1)
Factor out 5: = 5(2n + 1)(2n – 1)
= 5(4n² – 1)
= 20n² – 5
This is 20n² – 5 = (√(20n²))² – 5
But 20n² is not generally a perfect square unless n is special.
But noticing 20n² – 5 = (10n)² – 5
So the result is 5 less than the square (10n)²
So, statement (iv) is true.

6. A number leaves a remainder of 3 when divided by 7, and another number leaves a remainder of 5 when divided by 7. What is the remainder when their sum, difference, and product are divided by 7?
See AnswerLet the first number be: 7a + 3 (because it leaves remainder 3 when divided by 7)
Let the second number be: 7b + 5 (because it leaves remainder 5 when divided by 7)
Now we find the remainders of their sum, difference, and product when divided by 7.
Remainder of the sum = (7a + 3) + (7b + 5)
= 7a + 7b + 8
= 7(a + b) + 8
Now divide 8 by 7 → remainder is 1.
Remainder of the sum = 1
Remainder of the difference = (7a + 3) – (7b + 5)
= 7a – 7b – 2
= 7(a – b) – 2
Now –2 when divided by 7 leaves remainder 5.
Remainder of the difference = 5
Remainder of the product = (7a + 3)(7b + 5)
= 7a·7b + 7a·5 + 3·7b + 3·5
= 49ab + 35a + 21b + 15
= 7(7ab + 5a + 3b) + 15
15 divided by 7 → remainder is 1 (since 15 = 14 + 1)
Remainder of the product = 1.

7. Choose three consecutive numbers, square the middle one, and subtract the product of the other two. Repeat the same with other sets of numbers. What pattern do you notice? How do we write this as an algebraic equation? Expand both sides of the equation to check that it is a true identity.
See AnswerLet us take three consecutive numbers: 2, 3, 4
Middle = 3
So, 3² – (2 × 4) = 9 – 8 = 1
In 5, 6, 7
6² – (5 × 7) = 36 – 35 = 1
In 10, 11, 12
11² – (10 × 12) = 121 – 120 = 1
Every time, the answer is 1.
So we notice the pattern that the square of the middle number – product of the other two = 1 for any three consecutive numbers.
Writing it as an algebraic equation:
Let the three consecutive numbers be: n – 1, n, n + 1
According to the pattern: n² – (n – 1)(n + 1) = 1
This is an algebraic equation (identity).
Now expanding both sides:
Expand the product on the left: (n – 1)(n + 1) = n² – 1
Now put this into the equation: n² – (n² – 1)
= n² – n² + 1
= 1
So the left side becomes 1, which is exactly the right side.
Hence, For any three consecutive numbers n – 1, n, n + 1: n² – (n – 1)(n + 1) = 1.
Therefore, the pattern is a true identity.

8. What is the algebraic expression describing the following steps — add any two numbers. Multiply this by half of the sum of the two numbers? Prove that this result will be half of the square of the sum of the two numbers.
See AnswerLet the two numbers be a and b.
Sum = a + b
Half of the sum = 1/2(a + b)
Multiplying the sum by half of the sum = (a + b) × 1/2(a + b)
So the algebraic expression is (a + b) × 1/2(a + b)
Square of the sum is (a + b)²
Half of that is 1/2 (a + b)²
Now expanding the expression: (a + b) × 1/2(a + b)
= 1/2 (a + b)(a + b)
= 1/2 (a + b)²
This is exactly the same as half of the square of the sum.
Hence, the result is always half of the square of the sum of the two numbers.

9. Which is larger? Find out without fully computing the product.
(i) 14 × 26 or 16 × 24
(ii) 25 × 75 or 26 × 74
See Answer(i) In 14 × 26, the two numbers are unequal (difference = 12)
In 16 × 24, the two numbers are closer (difference = 8)
For a fixed sum, the product is larger when the numbers are closer.
Checking the sums:
14 + 26 = 40
16 + 24 = 40
Since both have the same sum (40), the pair closer to each other gives the bigger product.
16 and 24 are closer than 14 and 26.
So, 16 × 24 is larger.
(ii) Checking sums again:
25 + 75 = 100
26 + 74 = 100
Same sum.
Now comparing closeness:
25 and 75 → difference = 50
26 and 74 → difference = 48
26 and 74 are closer, so their product is larger.
So, 26 × 74 is larger.

10. A tiny park is coming up in Dhauli. The plan is shown in the figure. The two square plots, each of area g² sq. ft., will have a green cover. All the remaining area is a walking path w ft. wide that needs to be tiled. Write an expression for the area that needs to be tiled.

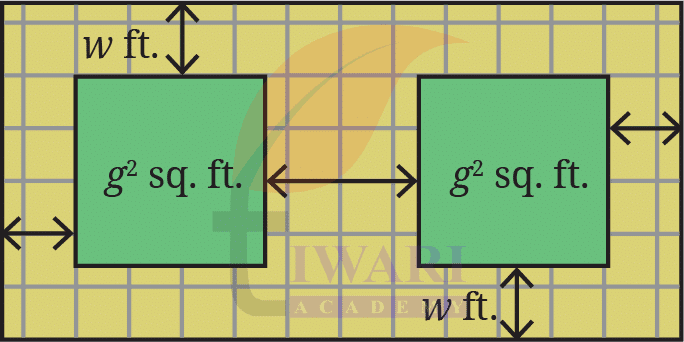
See AnswerEach green square has area g² sq. ft., so each side is g ft.
There is a w-ft wide walking path: on the left, on the right, above and below.
But a 2w-ft wide gap between the two squares (this is clearly shown in the diagram).
So for the outer rectangle of the whole park:
Total width = g (height of square) + w (top path) + w (bottom path)
= g + 2w
Total length = w (left path) + g (first square) + 2w (path in between) + g (second square) + w (right path)
So, the total length = 2g + 4w
Total area of the park = (total width) × (total length)
= (g + 2w)(2g + 4w)
Green area = 2 × g² = 2g²
Area to be tiled (walking path) = (g + 2w)(2g + 4w) – 2g².

11. For each pattern shown below,

(i) Draw the next figure in the sequence.
Answer:

(ii) How many basic units are there in Step 10?
See AnswerIf figure set I, the image are following the pattern of (k + 2)².
In first image k = 1, so number of squares = (1 + 2)² = 9
In second image k = 2, so number of squares = (2 + 2)² = 16
In third image k = 3, so number of squares = (3 + 2)² = 25
In fourth image k = 4, so number of squares = (4 + 2)² = 36
Similarly, In 10th image k = 10, so number of squares = (10 + 2)² = 144
If figure set II, the image are following the pattern of (k + 1)² + k.
In first image k = 1, so number of squares = (1 + 1)² + 1 = 5
In second image k = 2, so number of squares = (2 + 1)² + 2 = 11
In third image k = 3, so number of squares = (3 + 1)² + 3 = 19
In fourth image k = 4, so number of squares = (4 + 1)² + 4 = 29
Similarly, In 10th image k = 10, so number of squares = (10 + 1)² + 10 = 131.

(iii) Write an expression to describe the number of basic units in Step y.
See AnswerFor the image set I, step y = (k + 2)²
For the image set II, step y = (k + 1)² + k.