NCERT Solutions for Class 8 Maths Ganita Prakash Chapter 7 Proportional Reasoning-1

Page 159

Which images look similar and which ones look different?

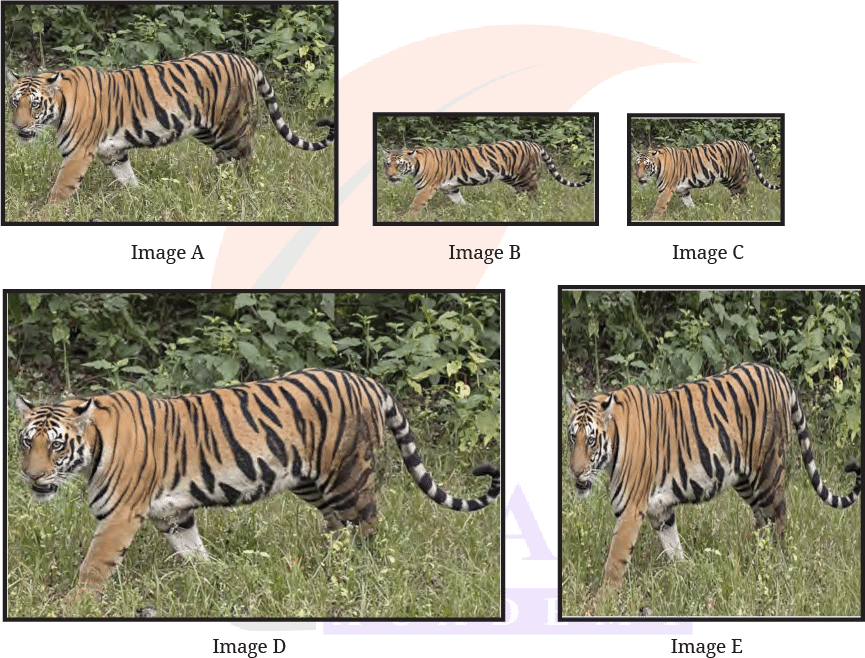
See AnswerImages that look similar: A, C and D. These three have the same height–width ratio, so their shape looks normal and similar to each other.
Images that look different: B and E.
Image B looks wider/stretched,
Image E looks taller/thinner.

Page 160

Do images B and E look like the other three images?
Why?
See AnswerNo, images B and E do not look like the other three images.
Images A, C, and D look similar in shape because their height–width ratio is the same. But in Image B, the tiger looks a bit wide and stretched. In Image E, the tiger looks a little tall and thin.
So their shapes don’t match the proportion of the other three, which is why B and E look different.

What makes images A, C, and D appear similar, and B and E different?
See AnswerThe height : width ratio of Image A, Image C and Image D comes out to be the same after simplifying.
Because their ratios match, the tiger in these images keeps the same shape—not stretched, not compressed—so they look similar.
Facts that makes B and E look different: Image B has a height–width ratio that becomes smaller, which means it looks wider sideways. Image E has a ratio that becomes larger, so it looks taller vertically.
Since their ratios do not match the ratio of A, C and D, the shapes get distorted, which makes B and E look different.

Can you check by what factors the width and height of image D change as compared to image A? Are the factors the same?
See AnswerWidth of A = 60 mm
Width of D = 90 mm
Width factor = 90 ÷ 60 = 3⁄2 = 1.5
Height of A = 40 mm
Height of D = 60 mm
Height factor = 60 ÷ 40 = 3⁄2 = 1.5
Both factors are the same (3⁄2).
So, the width and height of image D change by the same factor when compared to image A.

Page 161

By what factor should we multiply the ratio 60 : 40 (image A) to get 90 : 60 (image D)?
See AnswerRatio of image A = 60 : 40
Ratio of image D = 90 : 60
To find the factor, compare any one pair of corresponding terms:
Width factor = 90 ÷ 60 = 3⁄2
Height factor = 60 ÷ 40 = 3⁄2
Since both give the same value: Factor = 3⁄2 (which is 1.5)
So, we should multiply both terms of 60 : 40 by 3⁄2 to get 90 : 60.

Page 162

Example 1: Are the ratios 3 : 4 and 72 : 96 proportional?
See AnswerYes, the ratios 3 : 4 and 72 : 96 are proportional.
First ratio = 3 : 4
It is already in simplest form.
Second ratio = 72 : 96
Find the HCF of 72 and 96.
HCF = 24
Now divide both terms by 24:
72 ÷ 24 = 3
96 ÷ 24 = 4
So, the simplest form of 72 : 96 is also 3 : 4.
Both ratios become 3 : 4 in simplest form.

What is the HCF of 72 and 96?
See AnswerFactors of 72 → 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
Factors of 96 → 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 96
Common factors → 1, 2, 3, 4, 6, 8, 12, 24
The largest of these is 24.
So, HCF of 72 and 96 = 24.

Example 2: Kesang wanted to make lemonade for a celebration. She made 6 glasses of lemonade in a vessel and added 10 spoons of sugar to the drink. Her father expected more people to join the celebration. So he asked her to make 18 more glasses of lemonade.
To make the lemonade with the same sweetness, how many spoons of sugar should she add?
See AnswerKesang’s original mixture: 6 glasses of lemonade → 10 spoons of sugar
Now she needs 18 more glasses of lemonade.
To keep the same sweetness, the ratios must be proportional:
6 : 10 :: 18 : ?
First term changes from 6 to 18.
Factor = 18 ÷ 6 = 3
Multiply sugar by the same factor
10 × 3 = 30
So, she should add 30 spoons of sugar to make 18 more glasses of lemonade with the same sweetness.

How can we find the factor of change in the ratio?
See AnswerTo find the factor of change in a ratio, we compare how one term changes to the corresponding term in the new ratio.
Take the first terms of the two ratios and divide:
Factor of change = (new first term) ÷ (old first term)
Example from the lemonade problem:
Old ratio → 6 : 10
New ratio → 18 : ?
To find the factor: 18 ÷ 6 = 3
This number (3) is the factor of change.
Then we multiply the second term by the same factor.
So, we find the factor of change by dividing the new value by the original value.

Page 163

Example 3: Nitin and Hari were constructing a compound wall around their house. Nitin was building the longer side, 60 ft in length, and Hari was building the shorter side, 40 ft in length. Nitin used 3 bags of cement but Hari used only 2 bags of cement. Nitin was worried that the wall Hari built would not be as strong as the wall he built because she used less cement.
Is Nitin correct in his thinking?
See AnswerGiven:
Nitin’s wall → 60 ft, 3 bags of cement
Hari’s wall → 40 ft, 2 bags of cement
Nitin thinks Hari used less cement, so her wall might be weaker.
But we must check whether both used cement in the same proportion.
Nitin’s ratio (length : cement): 60 : 3
Hari’s ratio (length : cement): 40 : 2
For Nitin: 60 ÷ 3 = 20
So, 60 : 3 = 20 ft per bag
For Hari: 40 ÷ 2 = 20
So, 40 : 2 = 20 ft per bag
Both ratios give 20 ft per 1 bag of cement. This means both used cement at the same rate.
No, Nitin is not correct.
Hari used the same proportion of cement as Nitin. So her wall will be just as strong as his wall.

Example 4: In my school, there are 5 teachers and 170 students. The ratio of teachers to students in my school is 5 : 170. Count the number of teachers and students in your school. What is the ratio of teachers to students in your school? Write it below.
See AnswerIn my school:
Number of teachers = 20
Number of students = 600
So the ratio of teachers to students is 20 : 600
Divide both by 20:
20 ÷ 20 = 1
600 ÷ 20 = 30
So the simplest form of the ratio is 1 : 30
Therefore, Teachers : Students = 1 : 30.

Is the teacher-to-student ratio in your school proportional to the one in my school?
See AnswerGiven school’s ratio:
Teachers : Students = 5 : 170
Divide both by 5 → 1 : 34
So given school’s ratio = 1 : 34
My school’s ratio:
Teachers : Students = 1 : 30
These are not the same.

Example 5: Measure the width and height (to the nearest cm) of the blackboard in your classroom. What is the ratio of width to height of the blackboard?
See AnswerWidth of blackboard: 240 cm
Height of blackboard: 120 cm
Now the ratio of width to height is 240 : 120
Simplify by dividing both terms by 120:
240 ÷ 120 = 2
120 ÷ 120 = 1
So the simplest form of the ratio is Width : Height = 2 : 1.

Can you draw a rectangle in your notebook whose width and height are proportional to the ratio of the blackboard?
See AnswerSince my blackboard ratio is 2 : 1, I can draw any rectangle whose width is twice the height.
For example, in my notebook I draw:
Width = 10 cm
Height = 5 cm
Because 10 : 5 = 2 : 1, the same ratio as the blackboard.

Compare the rectangle you have drawn to those drawn by your classmates. Do they all look the same?
See AnswerWhen I compare my rectangle with my classmates’ rectangles:
► Some may draw 8 cm × 4 cm
► Some may draw 6 cm × 3 cm
► Some may draw 12 cm × 6 cm
Even though the sizes are different, the shape is the same because all of them follow the 2 : 1 proportional ratio.
So, yes, all rectangles drawn with the same ratio (2 : 1) will look the same in shape, even if the sizes are different. Only the scale changes, not the shape.

Page 164

Example 6: When Neelima was 3 years old, her mother’s age was 10 times her age. What is the ratio of Neelima’s age to her mother’s age? What would be the ratio of their ages when Neelima is 12 years old? Would it remain the same?
See AnswerWhen Neelima was 3 years old
Mother’s age = 10 × Neelima’s age
Mother’s age = 10 × 3 = 30 years
So the ratio of their ages is:
Neelima : Mother = 3 : 30
Simplify by dividing both by 3:
3 : 30 = 1 : 10
When Neelima is 12 years old
Since Neelima was 3 earlier, she has grown by: 12 − 3 = 9 years
Her mother will also increase by 9 years:
Mother’s earlier age = 30
Mother’s new age = 30 + 9 = 39
So new ratio: Neelima : Mother = 12 : 39
Simplify by dividing both by 3:
12 ÷ 3 = 4
39 ÷ 3 = 13
So the simplified ratio is 4 : 13.
Earlier ratio = 1 : 10
Later ratio = 4 : 13
These are not the same.

Example 7: Fill in the missing numbers for the following ratios that are proportional to 14 : 21.
______ : 42 6 : ______ 2 : ______
See AnswerGiven ratio 14 : 21.
Divide both by 7:
14 ÷ 7 = 2
21 ÷ 7 = 3
So 14 : 21 = 2 : 3
Now we have to use the simplified ratio 2 : 3 to fill the blanks.
► ___ : 42
We want the second term to be 42.
The original second term is 21.
Factor = 42 ÷ 21 = 2
Multiply the first term (14) by 2:
14 × 2 = 28
So the ratio is 28 : 42
► 6 : ____
We want the first term to be 6.
The original first term is 14.
Factor = 6 ÷ 14 = 3/7
Multiply the second term (21) by 3/7:
21 × 3/7 = 3 × 3 = 9
So the ratio is 6 : 9
► 2 : ____
We use the simplified ratio 2 : 3.
If the first term is 2, the second term must be 3.
So the ratio is 2 : 3.

What factor should we multiply 14 by to get 6? Can it be an integer? Or should it be a fraction?
See AnswerWe want to find the factor such that: 14 × (factor) = 6
So, factor = 6 ÷ 14 = 3 ÷ 7 = 3/7
3/7 is not an integer.
There is no integer you can multiply 14 by to get 6.
It must be a fraction and that fraction is 3/7.

Page 165

Why is this coffee stronger?
See AnswerNormal coffee:
Coffee decoction : Milk = 15 : 35
(Simplest form → divide by 5 → 3 : 7)
Stronger coffee:
Coffee decoction : Milk = 20 : 30
(Simplest form → divide by 10 → 2 : 3)
The second coffee stronger because in the stronger coffee, the amount of decoction is more compared to milk.
Let’s compare the simplified ratios:
Normal coffee → 3 parts decoction for 7 parts milk
Stronger coffee → 2 parts decoction for 3 parts milk
Normal coffee: Total parts = 3 + 7 = 10
Decoction part = 3/10 = 30%
Stronger coffee: Total parts = 2 + 3 = 5
Decoction part = 2/5 = 40%
So the stronger coffee has 40% decoction, while the normal one has 30%.

Why is this coffee lighter?
See AnswerNormal coffee ratio
Decoction : Milk = 15 : 35
Simplest form → 3 : 7
Decoction = 30%
Lighter coffee (more milk)
If he increases milk or reduces decoction, the ratio becomes something like:
Decoction : Milk = 10 : 40 (just an example)
Simplest form → 1 : 4
Decoction = 20%
This coffee become lighter because the amount of milk is much more compared to decoction and the percentage of decoction decreases.
This makes the coffee taste milder, thinner and less strong.

Page 165

1. Circle the following statements of proportion that are true.
(i) 4 : 7 :: 12 : 21
(ii) 8 : 3 :: 24 : 6
(iii) 7 : 12 :: 12 : 7
(iv) 21 : 6 :: 35 : 10
(v) 12 : 18 :: 28 : 12
(vi) 24 : 8 :: 9 : 3
See Answer(i) 4 : 7 :: 12 : 21
4 : 7 (already simplest) → 4 : 7
12 : 21 → divide by 3 → 4 : 7
True
(ii) 8 : 3 :: 24 : 6
8 : 3 (already simplest) → 8 : 3
24 : 6 → divide by 6 → 4 : 1
8 : 3 ≠ 4 : 1
False
(iii) 7 : 12 :: 12 : 7
7 : 12 (simplest) → 7 : 12
12 : 7 (simplest) → 12 : 7
7 : 12 ≠ 12 : 7
False
(iv) 21 : 6 :: 35 : 10
21 : 6 → divide by 3 → 7 : 2
35 : 10 → divide by 5 → 7 : 2
True
(v) 12 : 18 :: 28 : 12
12 : 18 → divide by 6 → 2 : 3
28 : 12 → divide by 4 → 7 : 3
2 : 3 ≠ 7 : 3
False
(vi) 24 : 8 :: 9 : 3
24 : 8 → divide by 8 → 3 : 1
9 : 3 → divide by 3 → 3 : 1
True

2. Give 3 ratios that are proportional to 4 : 9.
______ : ______ ______ : ______ ______ : ______
See Answer► 1st ratio (multiply by 2)
4 × 2 = 8
9 × 2 = 18
8 : 18
► 2nd ratio (multiply by 3)
4 × 3 = 12
9 × 3 = 27
12 : 27
► 3rd ratio (multiply by 5)
4 × 5 = 20
9 × 5 = 45
20 : 45.

3. Fill in the missing numbers for these ratios that are proportional to 18 : 24.
3 : ______ 12 : ______ 20 : ______ 27 : ______
See AnswerWe want all ratios to be proportional to 18 : 24.
18 ÷ 6 = 3
24 ÷ 6 = 4
So 18 : 24 = 3 : 4
Now we use the ratio 3 : 4 to fill in each blank.
► 3 : ______
This already matches the first term of 3 : 4.
So the second term must be 4.
3 : 4
► 12 : ______
Compare with 3 : 4.
Find factor: 12 ÷ 3 = 4
Multiply second term: 4 × 4 = 16
12 : 16
► 20 : ______
Find factor: 20 ÷ 3 = 20/3 (not an integer but allowed)
Multiply second term: 4 × (20/3) = 80/3
20 : 80/3
► 27 : ______
Find factor: 27 ÷ 3 = 9
Multiply second term: 4 × 9 = 36
27 : 36.

4. Look at the following rectangles. Which rectangles are similar to each other? You can verify this by measuring the width and height using a scale and comparing their ratios.

See AnswerRectangles that look similar in shape: C and D
Both are long, stretched rectangles with the same kind of proportion (long width compared to height). Even though they are rotated, rotation does not change similarity.
Rectangles that also look similar to each other: A and E
Both are tall, narrow rectangles with almost the same width-to-height ratio. E is just tilted, but tilting also does not affect similarity.
Rectangle B looks like a more regular, broad rectangle.
Its ratio does not visually match A, C, D or E.

5. Look at the following rectangle. Can you draw a smaller rectangle and a bigger rectangle with the same width to height ratio in your notebooks? Compare your rectangles with your classmates’ drawings.
Are all of them the same? If they are different from yours, can you think why? Are they wrong?

Answer:
We have to draw a smaller rectangle and a bigger rectangle. Both must have the same width : height ratio as the original rectangle. That means all rectangles should be similar (same shape, different size).

Even though all students use the same ratio, their rectangles but there are:
► shorter, taller, wider or longer
► drawn at different scales
► drawn in different orientations (vertical or horizontal)
So the rectangles may look different in size, but their shape will be the same if the ratio is correct.
A rectangle with the same width : height ratio can be drawn in many different sizes.
For Example if the ratio of the original rectangle is 4 : 3, then these are all correct:
8 : 6 or 12 : 9 or 20 : 15 or 40 : 30 and more.
Different numbers, same ratio → all are correct.
Only if someone does not keep the ratio the same, then the rectangle shape will change → that would be wrong.

6. The following figure shows a small portion of a long brick wall with patterns made using coloured bricks. Each wall continues this pattern throughout the wall. What is the ratio of grey bricks to coloured bricks? Try to give the ratios in their simplest form.

See Answer(a) Red bricks – There are 3 red clusters, each cluster having:
3 red bricks on top
2 red bricks below
1 red bricks at bottom
So each cluster = 3 + 2 + 1 = 6 red bricks
Grey bricks – Now count the grey bricks in the same portion:
2 grey bricks on top
3 grey bricks below
4 grey bricks at bottom
So each cluster = 2 + 3 + 4 = 9 grey bricks
Grey : Red = 9 : 6
Simplify by dividing both by 3:
9 ÷ 3 = 3
6 ÷ 3 = 2
So, the ratio for (a) = 2 : 1
(b) Grey bricks in each cluster = 16
Red bricks in each cluster = 12
So, Grey : Brown = 16 : 12
Simplify by dividing both by 4:
16 ÷ 4 = 4
12 ÷ 4 = 3
Therefore, the ratio for (b): 2 : 1.

7. Let us draw some human figures. Measure your friend’s body — the lengths of their head, torso, arms, and legs. Write the ratios as mentioned below—

See Answer► head : torso
Head = 20 cm
Torso = 40 cm
Ratio = 20 : 40 = 1 : 2
► torso : arms
Torso = 40 cm
Arms = 50 cm
Ratio = 40 : 50 = 4 : 5
► torso : legs
Torso = 40 cm
Legs = 80 cm
Ratio = 40 : 80 = 1 : 2.

Page 167

Does the drawing look more realistic if the ratios are proportional? Why? Why not?
See AnswerYes, the drawing definitely looks more realistic when the body-part ratios are proportional.
A real human body has natural proportions.
For example: Head is usually smaller than torso, Arms and legs have fixed proportional lengths and Torso is roughly twice the head, etc.
When you draw your figure using ratios that match real-life proportions, the parts fit together correctly.
So the drawing looks balanced, natural, and human-like.
It looks unrealistic when ratios are not proportional – If the ratios are wrong, for example: Head is too big or too small, Arms are too long and Legs are too short.
Then the drawing looks distorted or cartoonish, because the parts no longer match real human proportions.

Example 8: For the mid-day meal in a school with 120 students, the cook usually makes 15 kg of rice. On a rainy day, only 80 students came to school. How many kilograms of rice should the cook make so that the food is not wasted?
See AnswerGiven:
120 students → 15 kg rice
80 students → ? kg rice
Let the rice for 80 student = k kg
So, number of students : Rice = 120 : 15 :: 80 : k
⇒ 120/15 = 80/k
⇒ 120 k = 80 x 15
⇒ 120 k = 1200
⇒ k = 1200/120 = 10.

What is the factor of change in the first term?
See AnswerThe factor of change in the first term is 80 ÷ 120 = 2⁄3
So the factor of change is 2⁄3.

Page 169

Example 9: A car travels 90 km in 150 minutes. If it continues at the same speed, what distance will it cover in 4 hours?
See Answer4 hours = 4 × 60 = 240 minutes
90 km is covered in 150 minutes.
We have to find distance in 240 minutes.
So, 150 : 90 :: 240 : x
⇒ x = 90 × (240⁄150)
⇒ x = 90 × (8⁄5)
⇒ x = 18 × 8
⇒ x = 144.

Is this the right way to formulate the question?
See AnswerYes, this is the right way to formulate the question.
Distance increases when time increases, if speed stays the same.
So we compare the two situations like this:
150 minutes → 90 km
240 minutes → x km
This is the correct proportional method because distance is directly proportional to time when the speed does not change.

How can you find the distance covered in 240 minutes?
See AnswerThe car travels 90 km in 150 minutes.
First find the factor of change: 240 ÷ 150 = 8⁄5
Now multiply the distance by the same factor: 90 × 8⁄5 = 144
So, the distance covered in 240 minutes is 144 km.

Example 10: A small farmer in Himachal Pradesh sells each 200 g packet of tea for ₹200. A large estate in Meghalaya sells each 1 kg packet of tea for ₹800. Are the weight-to-price ratios in both places proportional? Which tea is more expensive?
See AnswerHimachal farmer: 200 g → ₹200
Meghalaya estate: 1 kg = 1000 g
1000 g → ₹800
For Himachal farmer: Price per gram = 200 ÷ 200 = ₹1 per gram
For Meghalaya estate: Price per gram = 800 ÷ 1000 = ₹0.8 per gram
Himachal ratio = 200 g : ₹200 = 1 g : ₹1
Meghalaya ratio = 1000 g : ₹800 = 1 g : ₹0.8
These ratios are not the same.
So, the weight-to-price ratios are not proportional.
Since the Himachal farmer charges ₹1 per gram and the Meghalaya estate charges ₹0.8 per gram, the Himachal tea is more expensive.

Page 170

Which tea is more expensive? Why?
See AnswerThe Himachal tea is more expensive because the Himachal farmer charges ₹1 for each gram of tea, while the Meghalaya estate charges ₹0.8 for each gram.
Since ₹1 per gram is more than ₹0.8 per gram, the Himachal tea costs more for the same amount of tea.

Page 170

1. The Earth travels approximately 940 million kilometres around the Sun in a year. How many kilometres will it travel in a week?
See AnswerEarth travels 940 million km in 1 year.
1 year = 52 weeks
Distance per week = 940 million ÷ 52 = 940 ÷ 52 ≈ 18.07
So, Distance ≈ 18.07 million kilometres.

2. A mason is building a house in the shape shown in the diagram. He needs to construct both the outer walls and the inner wall that separates two rooms. To build a wall of 10-feet, he requires approximately 1450 bricks. How many bricks would he need to build the house? Assume all walls are of the same height and thickness.

See AnswerFrom the diagram, the house is a rectangle 15 ft long and 12 ft wide, with one inner wall running from top to bottom and separating it into two rooms.
Outer walls (perimeter):
Lengths: 15 ft and 15 ft
Widths: 12 ft and 12 ft
Perimeter = 2 × (15 + 12) = 2 × 27 = 54 ft
Inner wall: Runs from top to bottom = 12 ft
Total wall length = 54 ft + 12 ft = 66 ft
We know that 10 ft of wall needs 1450 bricks
So, bricks per foot: 1450 ÷ 10 = 145 bricks per foot
Now for 66 ft, number of bricks = 66 × 145 = 9570 bricks.

Page 171

Puneeth’s father went from Lucknow to Kanpur in 2 hours by riding his motorcycle at a speed of 50 km/h. If he drives at 75 km/h, how long will it take him to reach Kanpur? Can we form this problem as a proportion — 50 : 2 :: 75 : __
See AnswerDistance from Lucknow to Kanpur is the same in both cases.
Speed and time are related as:
Higher speed → Less time
Lower speed → More time
So speed and time are inversely proportional, not directly proportional.
Checking if we can form a proportion like 50 : 2 :: 75 : __
No, we cannot.
This proportion assumes that speed and time increase or decrease together, but here speed increases and time decreases.
So the ratio 50 : 2 :: 75 : t is NOT correct.
This is a case of inverse proportion.
Speed₁ × Time₁ = Speed₂ × Time₂
⇒ 50 × 2 = 75 × t
⇒ 100 = 75t
⇒ t = 100 ÷ 75
⇒ t = 4/3 hours
⇒ t = 1 hour 20 minutes.

Activity 2: Go to the market and collect the prices of different sizes of shampoo containers of the same shampoo and create a table like the one given below. See if the volume of shampoo is proportional to the price.

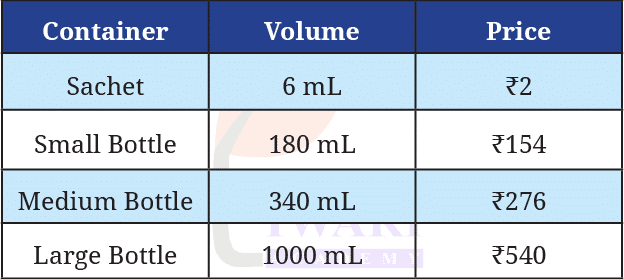
See AnswerFind price per mL for each size
1. Sachet: 2 ÷ 6 = 0.33 ₹/mL
2. Small Bottle: 154 ÷ 180 ≈ 0.86 ₹/mL
3. Medium Bottle: 276 ÷ 340 ≈ 0.81 ₹/mL
4. Large Bottle: 540 ÷ 1000 = 0.54 ₹/mL
If volume and price were proportional, price per mL should be the same for all containers.
But we have:
0.33 ₹/mL
0.86 ₹/mL
0.81 ₹/mL
0.54 ₹/mL
They are not equal.
So, volume is not proportional to price.

Page 172

Why do you think that the ratio of the prices is not proportional to the ratio of the volumes?
See AnswerThe ratio of prices is not proportional to the ratio of volumes because the price per mL is different for each container.
Small pouches and small bottles usually cost more per mL, while big bottles cost less per mL.
This happens because companies add extra costs for packaging, design and convenience.
A sachet needs more packaging material per mL than a 1-litre bottle, so it becomes costlier for a small amount.
Because of these extra packaging and marketing costs, the price does not increase in the same proportion as the volume. So, the ratios are not proportional.

Activity 3: Form a pair. Collect 12 countable objects or counters (it can be coins, seeds, or pebbles). Now, share them between the two of you in different ways.
If you divide them equally, what is the ratio of the number of counters with each of you?
See AnswerWe have 12 counters and we divide them equally between two people.
Each person gets: 12 ÷ 2 = 6 counters
So the ratio of counters with each person is 6 : 6
Now simplify it: 6 : 6 = 1 : 1
Therefore, the ratio of the number of counters with each person is 1 : 1.

If your partner gets 5 counters, how many objects will you get? What is the ratio of the counters?
See AnswerWe have a total of 12 counters.
If my partner gets 5 counters, then I get 12 − 5 = 7 counters
So the ratio of counters (me : partner) is 7 : 5.

Page 173

Now, if you want to share the counters between the two of you in the ratio of 3 : 1, how many counters would each of you get?
See AnswerWe want to divide 12 counters in the ratio 3 : 1.
First, adding the ratio parts: 3 + 1 = 4 parts
Now finding the value of 1 part: 12 ÷ 4 = 3 counters per part
Now multiply:
Person 1 gets 3 parts → 3 × 3 = 9 counters
Person 2 gets 1 part → 1 × 3 = 3 counters
Therefore, in the ratio 3 : 1, the counters are shared as 9 counters and 3 counters.

Now, if you want to share 42 counters between the two of you in the ratio of 4 : 3, how will you do it?
See AnswerAdding the ratio parts: 4 + 3 = 7 parts
42 counters ÷ 7 parts = 6 counters per part
So, first person gets 4 parts → 4 × 6 = 24 counters
Second person gets 3 parts → 3 × 6 = 18 counters.

What is the size of each group?
See AnswerWe are dividing 42 counters in the ratio 4 : 3.
Total parts = 4 + 3 = 7
So the size of each group (each part) is 42 ÷ 7 = 6 counters.

Page 174

Example 11: Prashanti and Bhuvan started a food cart business near their school. Prashanti invested ₹75,000 and Bhuvan invested ₹25,000. At the end of the first month, they gained a profit of ₹4,000. They decided that they would share the profit in the same ratio as that of their investment. What is each person’s share of the profit?
See AnswerPrashanti : Bhuvan = 75,000 : 25,000
Divide both numbers by 25,000:
75,000 ÷ 25,000 = 3
25,000 ÷ 25,000 = 1
So the investment ratio is 3 : 1.
Now, the total profit = ₹4,000
Total parts = 3 + 1 = 4 parts
Therefore, 1 part = 4,000 ÷ 4 = ₹1,000
So, Prashanti: 3 parts → 3 × 1,000 = ₹3,000
Bhuvan: 1 part → 1 × 1,000 = ₹1,000.

Example 12: A mixture of 40 kg contains sand and cement in the ratio of 3 : 1. How much cement should be added to the mixture to make the ratio of sand to cement 5 : 2?
See AnswerRatio = 3 : 1
Total parts = 3 + 1 = 4 parts
Each part = 40 ÷ 4 = 10 kg
So, Sand = 3 × 10 = 30 kg
Cement = 1 × 10 = 10 kg
Let x = amount of cement to be added
New cement = 10 + x
Sand stays the same = 30 kg
New ratio must be 5 : 2.
So, 30 : (10 + x) = 5 : 2
⇒ 30 × 2 = 5 × (10 + x)
⇒ 60 = 50 + 5x
⇒ 60 − 50 = 5x
⇒ 10 = 5x
⇒ x = 2
Therefore, we must add 2 kg of cement to make the ratio 5 : 2.

Page 175

1. Divide ₹4,500 into two parts in the ratio 2 : 3.
See AnswerTotal amount = 4500
Ratio = 2 : 3
Total parts = 2 + 3 = 5
Value of one part = 4500 ÷ 5 = 900
First share = 2 × 900 = 1800
Second share = 3 × 900 = 2700
So, the two parts are 1800 and 2700.

2. In a science lab, acid and water are mixed in the ratio of 1 : 5 to make a solution. In a bottle that has 240 mL of the solution, how much acid and water does the solution contain?
See AnswerThe ratio of acid to water is 1 : 5.
Total parts = 1 + 5 = 6 parts.
Total solution = 240 mL.
So, 1 part = 240 ÷ 6 = 40 mL.
Acid = 1 part = 40 mL.
Water = 5 parts = 5 × 40 = 200 mL.
Therefore, acid and water in the solution are 40 mL and 200 mL respectively.

3. Blue and yellow paints are mixed in the ratio of 3 : 5 to produce green paint. To produce 40 mL of green paint, how much of these two colours are needed? To make the paint a lighter shade of green, I added 20 mL of yellow to the mixture. What is the new ratio of blue and yellow in the paint?
See AnswerOriginal ratio = 3 : 5
Total parts = 3 + 5 = 8 parts
1 part = 40 ÷ 8 = 5 mL
Blue = 3 parts = 3 × 5 = 15 mL
Yellow = 5 parts = 5 × 5 = 25 mL
So, for 40 mL of green paint:
Blue = 15 mL
Yellow = 25 mL
After adding 20 mL of yellow:
Original yellow = 25 mL
Added yellow = 20 mL
New yellow = 25 + 20 = 45 mL
Blue stays the same = 15 mL
New ratio = 15 : 45 = 1 : 3.

4. To make soft idlis, you need to mix rice and urad dal in the ratio of 2 : 1. If you need 6 cups of this mixture to make idlis tomorrow morning, how many cups of rice and urad dal will you need?
See AnswerRatio of rice to urad dal = 2 : 1
Total parts = 2 + 1 = 3 parts
We need 6 cups of the mixture.
So, 1 part = 6 ÷ 3 = 2 cups
Rice = 2 parts = 2 × 2 = 4 cups
Urad dal = 1 part = 1 × 2 = 2 cups
Therefore, Rice = 4 cups
Urad dal = 2 cups.

5. I have one bucket of orange paint that I made by mixing red and yellow paints in the ratio of 3 : 5. I added another bucket of yellow paint to this mixture. What is the ratio of red paint to yellow paint in the new mixture?
See AnswerOriginal ratio of red : yellow = 3 : 5
So, Red = 3 parts
Yellow = 5 parts
Now we add another full bucket of yellow paint.
Let that added bucket be equal to 5 parts of yellow, so new amounts become:
Red = 3 parts
Yellow = 5 + 5 = 10 parts
New ratio = 3 : 10
Therefore, the new ratio of red paint to yellow paint is 3 : 10.

Page 176

Figure it Out
1. Anagh mixes 600 mL of orange juice with 900 mL of apple juice to make a fruit drink. Write the ratio of orange juice to apple juice in its simplest form.
See AnswerOrange juice = 600 mL
Apple juice = 900 mL
Ratio = 600 : 900
Now simplify by dividing both by 300:
600 ÷ 300 = 2
900 ÷ 300 = 3
Simplest form = 2 : 3
Therefore, the ratio of orange juice to apple juice in simplest form is 2 : 3.

2. Last year, we hired 3 buses for the school trip. We had a total of 162 students and teachers who went on that trip and all the buses were full. This year we have 204 students. How many buses will we need? Will all the buses be full?
See AnswerLast year: 3 buses carried 162 people.
So people per bus = 162 ÷ 3 = 54 people per bus
This year we have 204 students.
Number of buses needed = 204 ÷ 54
54 × 3 = 162
54 × 4 = 216
So 3 buses are not enough. So, we need 4 buses.
Total capacity of 4 buses = 4 × 54 = 216 people
We have 204 people.
Empty seats = 216 − 204 = 12
So the buses will not be full.

3. The area of Delhi is 1,484 sq. km and the area of Mumbai is 550 sq. km. The population of Delhi is approximately 30 million and that of Mumbai is 20 million people. Which city is more crowded? Why do you say so?
See AnswerFor Delhi:
Area = 1484 sq km
Population = 30 million
Population density = 30,000,000 ÷ 1484 ≈ 20,216 people per sq km
For Mumbai:
Area = 550 sq km
Population = 20 million
Population density = 20,000,000 ÷ 550 ≈ 36,363 people per sq km
Comparing densities:
Mumbai: ~36,363 people per sq km
Delhi: ~20,216 people per sq km
Mumbai has more people living in each square kilometre.
So, Mumbai is more crowded because it has a higher population density, meaning more people live in each square kilometre compared to Delhi.

4. A crane of height 155 cm has its neck and the rest of its body in the ratio 4 : 6. For your height, if your neck and the rest of the body also had this ratio, how tall would your neck be?
See AnswerRatio of neck : rest of body = 4 : 6
Total parts = 4 + 6 = 10 parts
1 part = 150 ÷ 10 = 15 cm
Neck = 4 parts = 4 × 15 = 60 cm
So, if my height is 150 cm, then my neck would be 60 cm tall in the 4 : 6 ratio.

5. Let us try an ancient problem from Lilavati. At that time weights were measured in a unit named palas and niskas was a unit of money. “If 2½ palas of saffron costs 3/7 niskas, O expert businessman! tell me quickly what quantity of saffron can be bought for 9 niskas?”
See Answer2½ palas of saffron costs 3⁄7 niskas.
⇒ 5⁄2 palas → 3⁄7 niskas
To get 1 niska, divide both sides by 3⁄7: (5⁄2) ÷ (3⁄7)
Dividing by a fraction means multiply by its reciprocal: (5⁄2) × (7⁄3)
= 35⁄6 palas per niska
So for each niska, you can buy 35⁄6 palas.
For 9 niskas, multiply by 9:
(35⁄6) × 9
= 35 × 9 ÷ 6
= 315 ÷ 6
= 52.5 palas
Therefore, for 9 niskas, one can buy 52.5 palas of saffron.

6. Harmain is a 1-year-old girl. Her elder brother is 5 years old. What will be Harmain’s age when the ratio of her age to her brother’s age is 1 : 2?
See AnswerLet Harmain’s future age = x years.
Right now:
Harmain = 1 year
Brother = 5 years
The age difference is 5 − 1 = 4 years
This difference will always stay the same.
We need the ratio = Harmain’s age : Brother’s age = 1 : 2
So when Harmain is x years old, her brother will be x + 4 years old
Now form the ratio:
x : (x + 4) = 1 : 2
⇒ x ÷ (x + 4) = 1 ÷ 2
⇒ 2x = x + 4
⇒ 2x − x = 4
⇒ x = 4
So, Harmain will be 4 years old when the ratio of her age to her brother’s age becomes 1 : 2.

7. The mass of equal volumes of gold and water are in the ratio 37 : 2. If 1 litre of water is 1 kg in mass, what is the mass of 1 litre of gold?
See AnswerThe ratio of masses (gold : water) = 37 : 2
This means, for the same volume, gold has 37 parts of mass and water has 2 parts of mass.
Now, 1 litre of water = 1 kg
So 2 parts = 1 kg
⇒ 1 part = 1 ÷ 2 = 0.5 kg
Gold has 37 parts, so mass of 1 litre of gold = 37 × 0.5 = 18.5 kg
Therefore, the mass of 1 litre of gold is 18.5 kg.

8. It is good farming practice to apply 10 tonnes of cow manure for 1 acre of land. A farmer is planning to grow tomatoes in a plot of size 200 ft by 500 ft. How much manure should he buy?
See AnswerLength = 200 ft
Width = 500 ft
Area = 200 × 500 = 100000 sq ft
We know that: 1 acre = 43560 sq ft
So, Area in acres = 100000 ÷ 43560
≈ 2.295 acres (about 2.3 acres)
Now, Good practice: 10 tonnes per acre
So manure required: 10 × 2.295 ≈ 22.95 tonnes
Therefore, the farmer should buy about 23 tonnes of manure.

9. A tap takes 15 seconds to fill a mug of water. The volume of the mug is 500 mL. How much time does the same tap take to fill a bucket of water if the bucket has a 10-litre capacity?
See AnswerTime to fill mug = 15 seconds
Volume of mug = 500 mL
Bucket capacity = 10 litres
1 litre = 1000 mL
So, 10 litres = 10000 mL
Now, 500 mL is filled in 15 seconds.
So, flow rate = 500 ÷ 15 = 100/3 mL per second (approximately)
Time = volume ÷ flow rate
= 10000 ÷ 100/3 = 300 seconds
= 300 ÷ 60 minutes = 5 minutes
Therefore, the tap takes 5 minutes to fill the 10-litre bucket.

10. One acre of land costs ₹15,00,000. What is the cost of 2,400 square feet of the same land?
See Answer1 acre = 43560 sq ft
Cost of 1 acre = ₹1500000
So, cost per sq ft = 1500000 ÷ 43560 ≈ ₹34.43 per sq ft
Therefore, the cost = 2400 × 34.43 ≈ ₹82632
Hence, the cost of 2400 square feet of the land is approximately ₹82,632.

11. A tractor can plough the same area of a field 4 times faster than a pair of oxen. A farmer wants to plough his 20-acre field. A pair of oxen takes 6 hours to plough an acre of land. How much time would it take if the farmer used a pair of oxen to plough the field? How much time would it take him if he decides to use a tractor instead?
See AnswerA pair of oxen takes 6 hours to plough 1 acre and the field is 20 acres.
So total time using oxen: 20 × 6 = 120 hours
A tractor is 4 times faster than oxen. If oxen take 6 hours per acre, tractor takes:
6 ÷ 4 = 1.5 hours per acre
Now for 20 acres: 20 × 1.5 = 30 hours
Therefore,
The time taken using oxen: 120 hours
The time taken using tractor: 30 hours.

12. The ₹10 coin is an alloy of copper and nickel called ‘cupro-nickel’. Copper and nickel are mixed in a 3 : 1 ratio to get this alloy. The mass of the coin is 7.74 grams. If the cost of copper is ₹906 per kg and the cost of nickel is ₹1,341 per kg, what is the cost of these metals in a ₹10 coin?
See AnswerRatio of copper to nickel = 3 : 1
Total parts = 3 + 1 = 4 parts
Mass of coin = 7.74 g
Mass of 1 part = 7.74 ÷ 4 = 1.935 g
Now, the mass of each metal:
Copper = 3 parts = 3 × 1.935 = 5.805 g
Nickel = 1 part = 1.935 g
We know that 1 kg = 1000 g
Copper: 5.805 g = 0.005805 kg
Nickel: 1.935 g = 0.001935 kg
Now the Copper price = ₹906 per kg
⇒ Cost of copper in coin = 0.005805 × 906 ≈ ₹5.26
Nickel price = ₹1341 per kg
⇒ Cost of nickel in coin = 0.001935 × 1341 ≈ ₹2.59
Therefore, cost of metals in one ₹10 coin: ₹5.26 + ₹2.59 = ₹7.85.