NCERT Textbook Solutions for Class 9 Maths Chapter 1 Number Systems updated for New Session 2025-26 in Hindi and English Medium. NCERT 9th Mathematics textbook chapter 1 introduces the concept of real numbers, including rational and irrational numbers and explains their properties in detail.
Class 9 Maths Chapter 1 Solutions
Class 9 Maths Exercise 1.1
1. Is zero a rational number? Can you write it in the form p/q, where p and q are integers and q ≠ 0?
See AnswerYes, zero is a rational number.
It can be written in the form of p/q, where p and q are integers and q ≠ 0.
For example: 0/1, 0/2, 0/5 are rational numbers.
2. Find six rational numbers between 3 and 4.
See AnswerFirst Method: To get six rational number between 3 and 4, the denominator must be 6 + 1 = 7.
Here, 3 = 21/7 and 4 = 28/7.
So, the six rational can be obtained by changing numerator from 22 to 27.
Therefore, the rational numbers are: 22/7, 23/7, 24/7, 25/7, 26/7, 27/7.
Alternative Method:
six rational numbers between 3 and 4 are 3.1, 3.2, 3.3, 3.4, 3.5 and 3.6.
3. Find five rational numbers between 3/5 and 4/5.
See AnswerBy converting these numbers into decimal, we have 3/5 = 0.6 and 4/5 = 0.8.
Hence, five rational numbers between 3/5 and 4/5 are 0.61, 0.62, 0.63, 0.64 and 0.65.
4. State whether the following statements are true or false. Give reasons for your answers.(i) Every natural number is a whole number. (ii) Every integer is a whole number. (iii) Every rational number is a whole number.
See Answer(i) True, as whole number is the collection of Natural numbers and 0.
(ii) False, because negative integers are not whole numbers.
(iii) False, rational numbers like 3/5, 2/3, 7/9 are not the whole numbers.
Class 9 Maths Exercise 1.2
1. State whether the following statements are true or false. Justify your answers.
(i) Every irrational number is a real number.
(ii) Every point on the number line is of the form √m, where m is a natural number.
(iii) Every real number is an irrational number.
See Answer(i) True, as the collection of all rational and irrational number is real numbers.
(ii) False, there are infinite number on number line between √2 and √3 that can’t be represented as √m, m being a natural number.
(iii) False, because real numbers can be rational also.
2. Are the square roots of all positive integers irrational? If not, give an example of the square root of a number that is a rational number.
See AnswerThe square roots of all positive integers are not irrational, for example √4 = 2, which is a rational number.
3. Show how √5 can be represented on the number line.
To represent √5 on number line, take OB = 2 units and make a perpendicular AB at B such that AB = 1 unit.
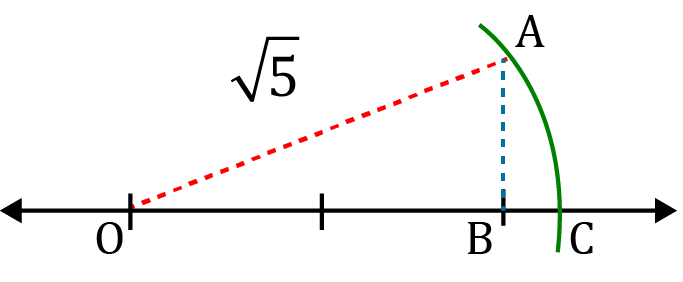
Now by Pythagoras theorem, the length of OA is √5. Now taking O as centre and OA as radius, mark an arc on OB, which intersects at C. Hence, OC = √5.
Class 9 Maths Exercise 1.3
1. Write the following in decimal form and say what kind of decimal expansion each has:
(i) 36/100 (ii) 1/11 (iii) 4 1/8 (iv) 3/13 (v) 2/11 (vi) 329/400
See Answer(i) 36/100 = 0.3, Terminating.
(ii) 1/11 = 0.0̄9̄99…, Recurring and Non-terminating.
(iii) 4 1/8 = 4.125, Terminating.
(iv) 3/13 = 0.2̄30769̄230769…, Recurring and Non-terminating.
(v) 2/11 = 0.1̄818…, Recurring and Non-terminating.
(vi) 329/400 = 0.8225, Terminating.
2. You know that 1/7 = 0.142857. Can you predict what the decimal expansions of 2/7, 3/7, 4/7, 5/7, 6/7 are?
See Answer2/7 = 2 × 1/7 = 2 × 0.142857̄ = 0.285714̄
3/7 = 3 × 1/7 = 3 × 0.142857̄ = 0.428571̄
4/7 = 4 × 1/7 = 4 × 0.142857̄ = 0.571428̄
5/7 = 5 × 1/7 = 5 × 0.142857̄ = 0.714285̄
6/7 = 6 × 1/7 = 6 × 0.142857̄ = 0.857142̄
3. Express the following in the form p/q, where p and q are integers and q ≠ 0.
(i) 0.6̄
See Answer(i) Let x = 0.6
⇒ x = 0.666… (i)
Multiplying equation (i) by 10 both sides
10x = 6.666…
10x = 6 + 0.6666… [From equation (i)]
10x – x = 6
9x = 6
⇒ x = 6/9 = 2/3
(ii) 0.47̄
See Answer(ii) 0.47
Let x = 0.47
⇒ x = 0.47777… (i)
Multiplying equation (i) by 10 both sides
10x = 4.7777… (ii)
Multiplying equation (ii) by 10 on both sides
100x = 47.777…
100x = 43 + 4.7777…
100x = 34 + 10x [From equation (ii)]
100x – 10x = 43
90x = 43
x = 43/90
(iii) 0.00̄1̄
See Answer(iii) Let x = 0.001001…
1000x = 1.001001…
1000x – x = 999x = 1
⇒ x = 1/999
4. Express 0.99999… in the form of p/q. Are you surprised by your answer? With your teacher and classmates discuss why the answer makes sense.
See Answer0.99999 … (i)
Multiplying equation (i) by 10 both sides
10x = 9 + 0.99999…
10x = 9 + x [From equation (i)]
10x – x = 9
9x = 9
x = 9/9 = 1
The answer makes sense as 0.99999… is very close to 1, that is why we can say that 0.9999 = 1.
5. What can be the maximum number of digits in the repeating block of digits in 1/17?Perform the division to check your answer?
See AnswerThe maximum number of digits is 16. (less than 17).
By performing the actual division, we get
1/17 = 0.0588235294117647
6. Look at several examples of rational numbers in the form of p/q (q≠0) where 𝑝 and 𝑞 are integers with no common factors other than 1 and having terminating decimal representations (expansions). Can you guess what property 𝑞 must satisfy?
See Answer2/5 = 0.4,
1/10 = 0.1,
3/2 = 1.5,
7/8 = 0.0875
The denominator of all the rational numbers are in the form of 2ᵐ × 5ⁿ, where 𝑚 and 𝑛 are integers.
7. Write three numbers whose decimal expansions are non-terminating non-recurring.
See Answer1. 0.41414114111114…
2. 2.01001000100001…
3. π = 3.1416…
8. Find three different irrational numbers between the rational numbers 5/7 and 9/11
See Answer5/7 = 0.714285, 9/11 = 0.81
We know that there are infinite many irrational numbers between two rational numbers. So the three irrational numbers are:
1) 0.72722722272222 …
2) 0.73733733373333 …
3) 0.74744744474444 …
9. Classify the following numbers as rational or irrational:
(i) √23 (ii) √225 (iii) 0.3796 (iv) 7.478478… (v) 1.10100100010001…
See Answer
(i) √23 – Irrational number
(ii) √225 = 15 – Rational number
(iii) 0.3796 – Rational number
(iv) 7.478478… = 7.478 – Rational number
(v) 1.10100100010001… – Irrational number
Class 9 Maths Exercise 1.4
1. Classify the following numbers as rational or irrational:
(i) 2 − √5
(ii) (3 − √23) − √23
(iii) 2√7/7√7
(iv) 1/√2
(v) 2𝜋
See Answer(i) 2 − √5 Irrational number.
(ii) (3 − √23) − √23 = 3 Rotational number.
(iii) 2√7/7√7 = 2/7 Rotational number.
(iv) 1/√2 Irrational number.
(v) 2𝜋 Irrational number.
2. Simplify each of the following expressions:
(i) (3 + √3)(2 + √2)
(ii) (3 + √3)(3 − √3)
(iii) (√5 + √2)2
(iv) (√5 − √2)(√5 + √2)
See Answer(i) (3 + √3)(2 + √2)
= 6 + 3√2 + 2√3 + √6
(ii) (3 + √3)(3 − √3)
= 3² − (√3)². [(a + b) (a – b) = a² – b²]
9 – 3 = 6
(iii) (√5 + √2)²
(√5 )² + (√2)² + 2 × √5 × √2 [(a + b)² = a² + b² + 2ab]
= 7 +2√10
(iv) (√5 − √2)(√5 + √2
= (√5 )² – (√2)² [(a – b) (a + b) = a² – b²]
= 5 – 2 = 3
3. Recall, 𝜋 is defined as the ratio of the circumference (say c) of a circle to its diameter (say d). That is 𝜋 =𝑐/𝑑. This seems to contradict the fact that 𝜋 is irrational. How will you resolve this contradiction?
See AnswerWith a scale or tape we get only an approximate rational number as the result of our measurement.
That is why 𝜋 can be approximately represented as a quotient of two rational numbers.
As a matter of mathematical truth it is irrational.
4. Represent √9.3 on the number line.
See AnswerTo represent √9.3 on the number line, draw AB = 9.3 units. Now produce AB to C, such that BC = 1 unit. Draw the perpendicular bisector of AC which intersects AC at O. Taking O as centre and OA as radius, draw a semi-circle which intersects D to the perpendicular at B. Now taking O as centre and OD as radius, draw an arc, which intersects AC produced at E. Hence, OE = √9.3.

5. Rationalise the denominators of the following:
(i) 1/√7
(ii) 1/√7−√6
(iii) 1/√5+√2
(iv) 1/√7−2
See Answer (i) 1/√7
= 1/√7 × √7/√7
= √7/7
(ii) 1/√7−√6
= 1/√7−√6 × √7+√6/√7+√6
= √7+√6/ (√7)² – (√6)²
= √7+√6/7 – 6
= √7 + √6
(iii) 1/√5+√2
= 1/√5+√2 × √5−√2/√5−√2
= √5−√2/ (√5)² – (√2)²
= √5−√2/5 – 2
= √5−√2/3
(iv) 1/√7−2 = 1/√7−2 × √7+2/√7+2
= √7+2/(√7)² − (2)²
= √7+2/7−4
= √7+2/3
Class 9 Maths Exercise 1.5
1. Find:
(i) 64¹/²
See Answer(i) 64¹/²
= (8²)¹/²
= 8²×¹/²
= 8
(ii) 32¹/⁵
See Answer(ii) 32¹/⁵
= (2⁵)¹/⁵
= 2⁵×¹/⁵
= 2
(iii) 125¹/³
See Answer(iii) 125¹/³
= (5³)¹/³
= 5³×¹/³
= 5
2. Find:
(i) 9³/²
See Answer(i) 9³/²
= (3²)³/²
= 3²×³/²
= 3²
= 9
(ii) 32⁵/²
See Answer(ii) 32⁵/²
= (2⁵)²/⁵
= 2⁵ײ/⁵
= 2²
= 4
(iii) 16³/⁴
See Answer(iii) 16³/⁴
= (2⁴)³/²
= 2⁴ ׳/⁴
= 2³
= 8
(iv) 125⁻¹/³
See Answer(iv) 125⁻¹/³
= (5³)⁻¹/³
= 5³×−¹/³
= 5⁻¹
= 1/5
= 5
3. Simplify:
(i) 2²/³.2¹/⁵
See Answer(i) 2²/³.2¹/⁵
= 2²/³ ⁺ ¹/⁵
= 2⁽¹⁰ ⁺ ³⁾/¹⁵
= 2¹³/¹⁵
(ii) (1/3³)⁷
See Answer(ii) (1/3³)⁷
= (3⁻³)⁷
= 3⁻²¹
(iii) 11¹/²/11¹/⁴
See Answer(iii) 11¹/²/11¹/⁴
= 11¹/² × 11⁻¹/⁴
= 11¹/² ⁻ ¹/⁴
= 11 ⁽²⁻¹⁾/⁴
= 11 ¹/⁴
(iv) 7¹/². 8¹/²
See Answer(iv) 7¹/². 8¹/²
= (7 × 8)¹/²
= 56¹/²
Exercise 1.1 in English
Exercise 1.2 in English
Exercise 1.3 in English
Exercise 1.4 in English
Exercise 1.5 in English
For students seeking reliable study material, Class 9 NCERT Mathematics Chapter 1 Solutions in PDF format serve as a comprehensive guide. These NCERT Class 9th Maths Chapter 1 Solutions explain important topics like decimal expansion, laws of exponents and the representation of numbers on the number line. Whether studying offline or online, students can access Class 9 Math NCERT Book Chapter 1 Exercise Solutions Free PDF to resolve their queries.
Class 9 Maths Chapter 1 Solution for State Boards
The step-by-step NCERT Solutions for Class 9 Math Chapter 1 Number Systems not only simplify difficult problems but also help in scoring better grades. Number Systems Class 9 NCERT Mathematics Solutions are curated by experts and align with the latest syllabus, ensuring that every topic is covered thoroughly. These resources are a must-have for students aiming for excellence in mathematics.
Class 9 Maths Chapter 1 Exercise 1.1
Class 9 Maths Chapter 1 Exercise 1.2
Class 9 Maths Chapter 1 Exercise 1.3
Class 9 Maths Chapter 1 Exercise 1.4
Class 9 Maths Chapter 1 Exercise 1.5
Class 9 Maths Chapter 1 Exercise 1.6
NCERT Solutions for Class 9 Mathematics Chapter 1 are now easily available for free download, offering unparalleled assistance to students. The comprehensive Class 9 NCERT Maths Chapter 1 Solutions PDF Download covers all exercises in detail, ensuring students grasp every concept with clarity. Designed to simplify complex concepts, these NCERT Math Class 9th Exercise Chapter 1 Solutions PDF explain the fundamentals of rational and irrational numbers, making them easy to understand.
Class 9 Maths Chapter 1 Solution in Hindi
9th Class NCERT Mathematics textbook solutions also include solved examples that help students tackle challenging problems with confidence. Whether you’re looking for Number Systems NCERT Class 9 Solutions PDF for practice or a guide to enhance your understanding, these materials serve all purposes. With Class 9 Maths Chapter 1 Solutions NCERT, preparing for exams becomes a seamless process, fostering a deeper appreciation for the subject.
Class 9 Maths Exercise 1.1 in Hindi
Class 9 Maths Exercise 1.2 in Hindi
Class 9 Maths Exercise 1.3 in Hindi
Class 9 Maths Exercise 1.4 in Hindi
Class 9 Maths Exercise 1.5 in Hindi
Important Points in Class 9 Maths Chapter 1 for School Exams
Real Numbers: Understanding rational and irrational numbers.
Decimal Expansions: Terminating and non-terminating decimals.
Number Line Representation: Placing real numbers accurately.
Laws of Exponents: Applying exponent rules for real numbers.
Simplification: Using properties of roots and powers effectively.
| Day | Topics to Cover | Key Activities | Time Allocation |
|---|---|---|---|
| Day 1 | Introduction to Real Numbers | Understand rational and irrational numbers, examples and properties. | 1-2 hours |
| Day 2 | Decimal Expansions | Practice problems on terminating and non-terminating decimals. | 1.5-2 hours |
| Day 3 | Representation of Numbers on the Number Line | Learn methods to plot real numbers and solve exercises. | 1-2 hours |
| Day 4 | Laws of Exponents for Real Numbers | Revise exponent rules and solve related numerical problems. | 2-3 hours |
| Day 5 | Practice Questions | Attempt NCERT exercise problems and additional practice sets. | 2-3 hours |
| Day 6 | Revision | Review key concepts and solve sample papers. | 2-3 hours |
NCERT Revised Solutions for Class 9 Maths Chapter 1
NCERT Textbook Solutions for Class 9 Maths Chapter 1 Number Systems in Hindi Medium and English medium has been updated for academic session 2025-26. Tiwari Academy is a popular online platform that provides educational resources and solutions for students. As we continue to offer Class 9 Maths NCERT Exercises Solutions, here are some potential benefits of using Tiwari Academy for learning Class 9 Maths. Question-answers and solutions are modified as per revised NCERT book published for 2025-26 syllabus. We typically provides simple yet complete solutions to NCERT textbooks, including step-by-step explanations for each problem. This can be especially helpful for students who may find difficulty in understanding certain concepts.

| Class: 9 | Mathematics |
| Chapter 1: | Number Systems |
| Number of Exercises: | 5 (Five) |
| Content: | NCERT Textbook Solutions |
| Mode of Content: | Videos and Online Text Format |
| Academic Year: | Session 2025-26 |
| Medium: | English and Hindi Medium |
All the Solutions for Class 9th Maths Chapter 1 have been updated according to latest CBSE Curriculum and NCERT Books for 2025-26. Since UP Board Students are using same NCERT Textbooks, they can also download UP Board Solutions for Class 9 Maths Chapter 1 in Hindi Medium or English Medium. Class 9 Maths NCERT Revised Solutions have been provided by explaining the formulae and giving step by step explanation.
9th Maths Chapter 1 Solutions in English and Hindi Medium
The content is according to the latest CBSE syllabus for the students of CBSE Board as well as UP Board and MP Board following the updated NCERT (https://ncert.nic.in/) Books for their final exams. Solutions for chapter 1 9th Maths are available in PDF format on our website Tiwari Academy and also through videos on Apps and website.
About 9th Maths Chapter 1 Solutions
The topic Number Systems is the basis of Arithmetic. It is like learning the alphabets of any mathematics. We can say that 9th Maths chapter 1 is the foundation of Maths for secondary classes.
CBSE NCERT Solutions for Class 9 mathematics Chapter 1 Number Systems in PDF format. These solutions are available for free download for session 2025-26. These are updated as per latest curriculum. Kindly visit the Discussion Forum and become a partner in knowledge sharing in mathematics. NCERT Solutions Offline Apps 2025-26, work without internet connection. Everything on Tiwari Academy website and Apps are available free of cost. No login or registration is required.
Important Questions on 9th Maths Chapter 1
Is zero a rational number? Can you write it in the form p/q, where p and q are integers and q≠0?
Yes, zero is a rational number. It can be written in the form of p/q. For example: 0/1, 0/2, 0/5 are rational numbers, where p and q are integers and q≠0.
Simplify each of the following expression: (3 + √3)(2 + √2)
(3 + √3)(2 + √2)
= 6 + 3√2 + 2√3 + √6
Find six rational numbers between 3 and 4.
Six rational numbers between 3 and 4 are 3.1, 3.2, 3.3, 3.4, 3.5 and 3.6.
Express 0.99999… in the form of p/q . Are you surprised by your answer?
0.99999… Let x = 0.99999… … (i) Multiplying equation (i) by 10 both sides 10x = 9.99999… ⇒ 10x = 9 + 0.99999…… ⇒ 10x = 9 + x [From equation (i)] ⇒ 10x – x = 9 ⇒ 9x = 9 ⇒ x = 9/9 = 1 The answer makes sense as 0.99999… is very close to 1, that is why we can say that 0.99999=1.
Write three numbers whose decimal expansions are non-terminating non-recurring.
Three non-terminating non-recurring decimals: 0.414114111411114… 2.01001000100001… π=3.1416…
Important Terms on 9th Maths Chapter 1
1. Natural numbers are those numbers which are used for counting.
2. Whole numbers are the collection of all natural numbers together with zero.
3. Integers are the collection of all whole numbers and negative of natural numbers.
4. Rational numbers are those numbers which can be expressed in the form of p/q, where p, q are integers and q is not equal to 0.
5. Irrational numbers are those numbers which cannot be expressed in the form of p/q, where p, q are integers and q is not = 0.
6. Real numbers are the collection of all rational and irrational numbers.
Do you know?
Two numbers are said to be equivalent, if numerators and denominators of both are in proportion or they are reducible to be equal.
The decimal expansion of real numbers can be terminating or non-terminating repeating or non-terminating non-repeating.
The decimal expansion of rational numbers can either be terminating or non-terminating and vice-versa.
The decimal expansion of irrational numbers can either be non-recurring and vice-versa.
More to know?
If a is a rational and b is an irrational, then a + b and a – b are irrational, and ab and a/b are irrational numbers, where b is not equal to 0. If a and b both are irrational, then a+b, a-b, ab and a/b may be rational or irrational. If a be any real number and n be any positive integer such that a^1/n = n√a is a real number, then ‘n’ is called exponent, a is called radical and √ is called radical sign.
What topics are covered in NCERT Solutions for Class 9 Maths Chapter 1 Number Systems?
The NCERT Solutions for Class 9 Maths Chapter 1 Number Systems cover key topics like rational and irrational numbers, their decimal expansions and how to represent them on the number line. It also explains the properties of real numbers and laws of exponents for real numbers in detail. Students learn methods to simplify complex problems using these properties. The chapter provides a strong foundation for understanding advanced mathematical concepts, making it essential for academic success. By practicing these solutions, students gain a comprehensive understanding of the Number Systems, ensuring they excel in their exams.
How many questions in each exercise are given in chapter 1 of class 9 Maths?
There are 6 exercises in chapter 1 (Number systems) of class 9 Maths.
In the first exercise (Ex 1.1), there are four questions.
In the second exercise (Ex 1.2), there are four questions.
In the third exercise (Ex 1.3), there are nine questions.
In the fifth exercise (Ex 1.4), there are five questions.
In the sixth exercise (Ex 1.5), there are three questions.
So, there are in all 25 questions in chapter 1 (Number systems) of class 9 Maths.
There are in all 20 examples in chapter 1 (Number systems) of class 9 Maths.
How can NCERT Solutions for Class 9 Maths Chapter 1 help in exam preparation?
NCERT Revised Solutions for Class 9 Maths Chapter 1 Number Systems are an excellent tool for exam preparation. They provide step-by-step explanations for all exercise questions, enabling students to grasp concepts clearly and effectively. The solutions include solved examples and additional practice questions, which help students familiarize themselves with the types of problems commonly asked in exams. With NCERT Class 9 Maths Chapter 1 Solutions, students can identify and work on their weak areas. Available in PDF format, these resources are accessible anytime, making them ideal for last-minute revisions and thorough preparation.
What are the core topics to study in chapter 1 Number systems of class 9 Mathematics?
In chapter 1, Number systems of class 9 Maths, students will study:
1. Natural Numbers, Whole Numbers, Integers, Rational Numbers.
2. Irrational Numbers.
3. Real Numbers and their Decimal Expansions.
4. Representing Real Numbers on the Number Line.
5. Operations on Real Numbers.
6. Laws of Exponents for Real Numbers.
Where can I find NCERT Solutions for Class 9 Maths Chapter 1 in PDF format?
NCERT Solutions for Class 9 Maths Chapter 1 are widely available in PDF format online. These solutions can be downloaded for free from educational websites, ensuring easy access for students. The PDF format allows students to study both online and offline, providing a convenient way to prepare for exams. These Class 9 Maths Chapter 1 Solutions Free PDFs are comprehensive, covering all exercises and providing detailed answers. Whether for revision or regular practice, the downloadable PDFs are an invaluable resource for students aiming to strengthen their understanding of Number Systems.
Is chapter 1 of class 9th Maths difficult to solve?
Chapter 1 of class 9th Maths is not easy and not difficult. It lies in the middle of easy and difficult because some examples and questions of this chapter are easy, and some are difficult. However, the difficulty level of anything varies from student to student. So, Chapter 1 of class 9th Maths is easy or not depends on students also. Some students find it difficult, some find it easy, and some find it in the middle of easy and difficult.
Are the NCERT Solutions for Class 9 Maths Chapter 1 sufficient for board exams?
Yes, NCERT Solutions for Class 9 Maths Chapter 1 are sufficient for board exams as they strictly follow the NCERT syllabus and exam pattern. These solutions are designed to cover all the important concepts in a clear and concise manner, ensuring students have a thorough understanding of the chapter. The NCERT Class 9 Maths Chapter 1 Solutions PDF includes solved examples and practice problems, helping students prepare for a variety of questions. While these solutions provide a solid foundation, combining them with regular practice and mock tests can further enhance exam readiness.
How long it takes to study chapter 1 of class 9th Maths?
Students need a maximum of eight days to do chapter 1 of class 9th Maths if they give at least 2 hours per day to this chapter. This time also depends on student’s speed, efficiency, capability, and many other factors.


