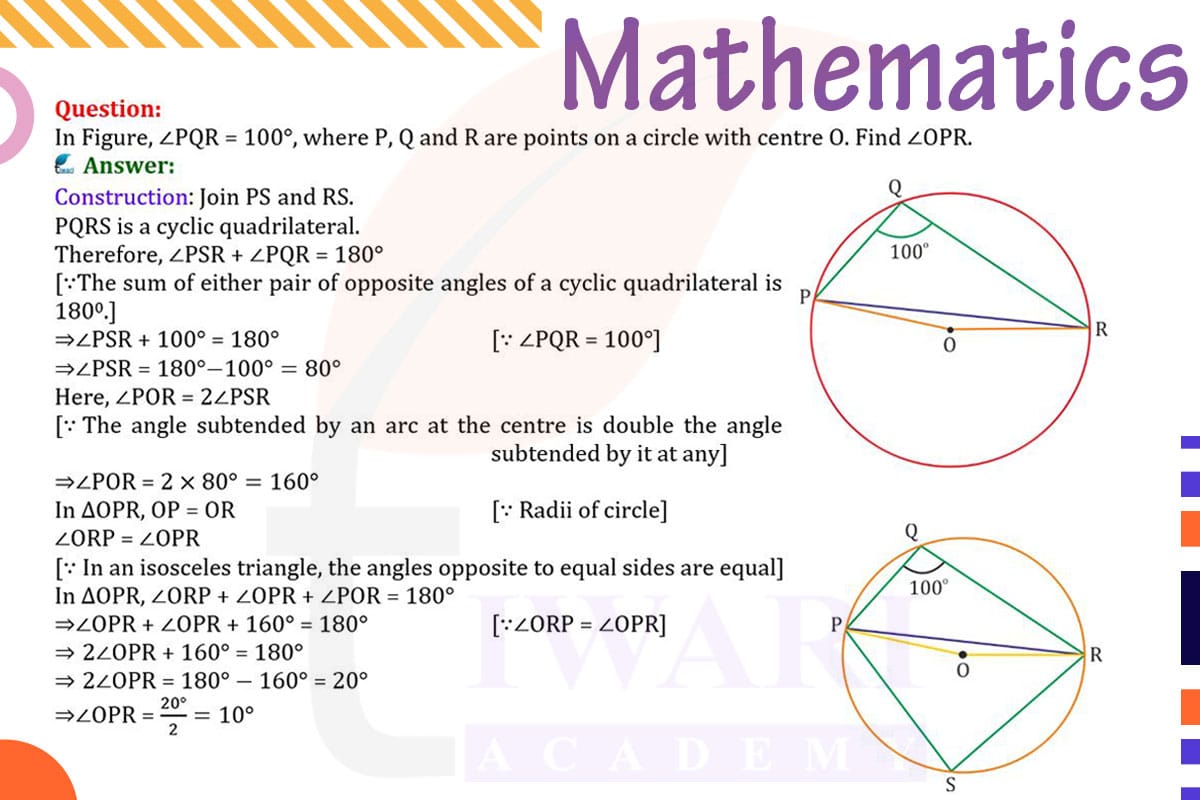
To find ∠OPR when ∠PQR = 100° in a circle with center O, we use the fact that the angle at the center of a circle is twice the angle at the circumference standing on the same arc. Here, ∠PQR stands on arc PR.
Since ∠PQR = 100°, the angle at the center, ∠POR (which also stands on arc PR), is twice ∠PQR. Therefore, ∠POR = 2 × 100° = 200°.
∠OPR is half of ∠POR because OPR is an isosceles triangle (OP and OR are radii of the circle and hence equal). So, ∠OPR = 200°/2 = 100°.
Let’s discuss in detail
Circle Geometry and Angle Calculation
In circle geometry, understanding the relationship between angles at the center and angles at the circumference is crucial. In this scenario, we have a circle with center O and points P, Q, and R on its circumference, forming an angle ∠PQR of 100°. The objective is to determine the measure of ∠OPR, which involves applying fundamental principles of circle geometry. This type of problem is common in geometric studies and provides insight into the symmetrical properties of circles.
The Relationship Between Central and Circumferential Angles
A key principle in circle geometry is that the angle at the center of a circle is twice the angle at the circumference when both angles stand on the same arc. This relationship is vital in solving problems involving angles in circles. In our case, ∠PQR is an angle at the circumference standing on arc PR, and we need to relate it to the corresponding central angle ∠POR.
Determining the Central Angle ∠POR
To find the central angle ∠POR, which also stands on arc PR, we use the principle that the central angle is twice the corresponding circumferential angle. Since ∠PQR is given as 100°, the central angle ∠POR is calculated as 2 × 100° = 200°. This calculation is a direct application of the central-to-circumferential angle relationship in circle geometry.
Understanding the Isosceles Triangle OPR
Triangle OPR is an isosceles triangle because OP and OR are radii of the circle and, therefore, are equal in length. In an isosceles triangle, the angles opposite the equal sides are also equal. This property of isosceles triangles plays a crucial role in determining the measure of ∠OPR.
Calculating ∠OPR
Since triangle OPR is isosceles with OP = OR, the angle ∠OPR is half of the central angle ∠POR. This is because the central angle is split equally between the two angles at the base of the isosceles triangle. Therefore, ∠OPR is 200° / 2 = 100°. This result is obtained by applying the properties of isosceles triangles to the triangle formed by the radii and the chord.
Applying Geometric Principles
In conclusion, by applying fundamental principles of circle geometry and the properties of isosceles triangles, we find that ∠OPR is 100°. This problem illustrates the elegance and consistency of geometric relationships, particularly in the context of circles. Understanding these principles allows for a deeper appreciation of the symmetry and patterns inherent in geometric shapes, and highlights the practical application of geometry in solving real-world problems.
Discuss this question in detail or visit to Class 9 Maths Chapter 9 for all questions.
Questions of 9th Maths Exercise 9.3 in Detail


