Two circles intersect at two points B and C. Through B, two line

Updated on January 6, 2024
by Tiwari Academy

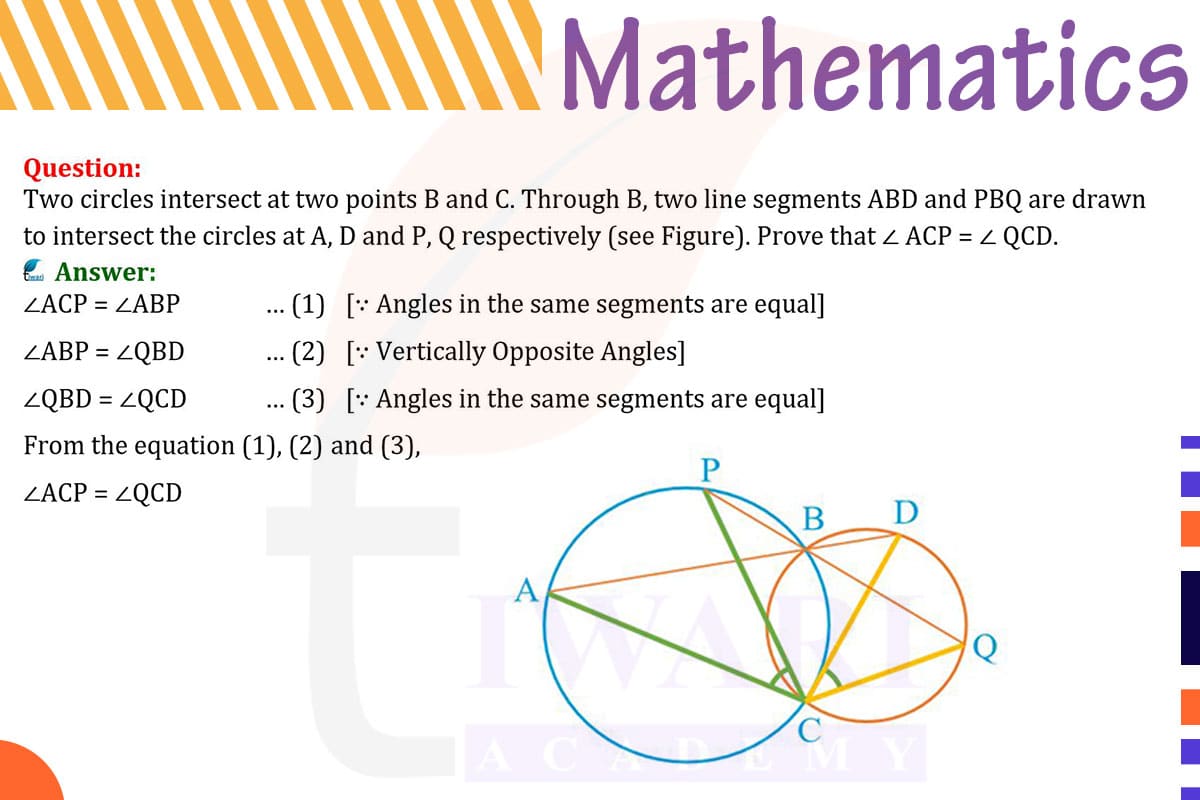
To prove ∠ACP = ∠QCD in two intersecting circles where line segments ABD and PBQ pass through the intersection point B, we use the property of angles in the same segment of a circle being equal.
Since A, B, C, and D lie on the circumference of one circle, and angles in the same segment are equal, ∠ACB = ∠ADB. Similarly, in the second circle, where P, B, C, and Q lie on the circumference, ∠PCB = ∠QCB.
Since B and C are intersection points of the circles, ∠ACB = ∠PCB. Therefore, ∠ADB = ∠QCB.
In triangle ACD, ∠ACP + ∠ADB = 180° (linear pair). Similarly, in triangle QCD, ∠QCD + ∠QCB = 180°. Since ∠ADB = ∠QCB, it follows that ∠ACP = ∠QCD.

Two circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively.

Let’s discuss in detail

Intersecting Circles and Line Segments

In the realm of circle geometry, the configuration of intersecting circles presents intriguing scenarios. In this specific case, we have two circles intersecting at points B and C. Through point B, two line segments ABD and PBQ are drawn, intersecting the circles at points A, D, and P, Q, respectively. Our objective is to prove that ∠ACP is equal to ∠QCD. This problem involves applying fundamental principles of circle geometry, particularly those related to angles formed by chords in intersecting circles.

Understanding Angles in the Same Segment

A key concept in circle geometry is that angles in the same segment of a circle are equal. This means that any angle formed at the circumference by the same chord will have the same measure. In our scenario, since points A, B, C, and D lie on the circumference of one circle, and points P, B, C, and Q lie on the circumference of the other, this principle can be applied to both sets of points.

Analyzing Angles in the First Circle

Focusing on the first circle, where A, B, C, and D lie, we apply the principle of angles in the same segment. Here, ∠ACB and ∠ADB are angles in the same segment, subtended by chord AB. According to the principle, these angles are equal, so ∠ACB = ∠ADB. This equality is a crucial step in our proof, establishing a relationship between the angles in the first circle.

Examining Angles in the Second Circle
Similarly, in the second circle containing points P, B, C, and Q, we examine the angles ∠PCB and ∠QCB. These are also angles in the same segment, subtended by chord PB. By the same principle, these angles are equal, so ∠PCB = ∠QCB. This step mirrors our analysis in the first circle and is essential for drawing parallels between the two intersecting circles.

Relating Angles Across the Circles

Since points B and C are the intersection points of the circles, the angles ∠ACB and ∠PCB are actually the same angle. Therefore, ∠ACB = ∠PCB implies that ∠ADB = ∠QCB. In triangles ACD and QCD, considering the linear pairs formed, we have ∠ACP + ∠ADB = 180° and ∠QCD + ∠QCB = 180°. The established equality of ∠ADB and ∠QCB leads us to the conclusion that ∠ACP must equal ∠QCD.

Proving Angle Equality in Intersecting Circles

In conclusion, by applying the principle of angles in the same segment and analyzing the relationships between angles in intersecting circles, we have successfully proven that ∠ACP is equal to ∠QCD. This proof not only demonstrates the consistency and elegance of geometric principles but also highlights the interconnectedness of angles and segments in circle geometry. Such problems underscore the depth and beauty of geometry, revealing how simple principles can lead to profound insights about shapes and their properties.

Discuss this question in detail or visit to Class 9 Maths Chapter 9 for all questions.
Questions of 9th Maths Exercise 9.3 in Detail

In Figure, A,B and C are three points on a circle with centre O such that ∠ BOC = 30° and ∠ AOB = 60°. If D is a point on the circle other than the arc ABC, find ∠ADC.

A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.

In Figure, ∠PQR = 100°, where P, Q and R are points on a circle with centre O. Find ∠OPR.

In Figure, ∠ABC = 69°, ∠ACB = 31°, find ∠BDC.

In Figure, A, B, C and D are four points on a circle. AC and BD intersect at a point E such that ∠BEC = 130° and ∠ECD = 20°. Find ∠BAC.

ABCD is a cyclic quadrilateral whose diagonals intersect at a point E. If ∠DBC = 70°, ∠BAC is 30°, find ∠BCD. Further, if AB = BC, find ∠ECD.

If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.

If the non-parallel sides of a trapezium are equal, prove that it is cyclic.

Two circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively. Prove that ∠ACP = ∠QCD.

If circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.

ABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠CAD = ∠CBD.