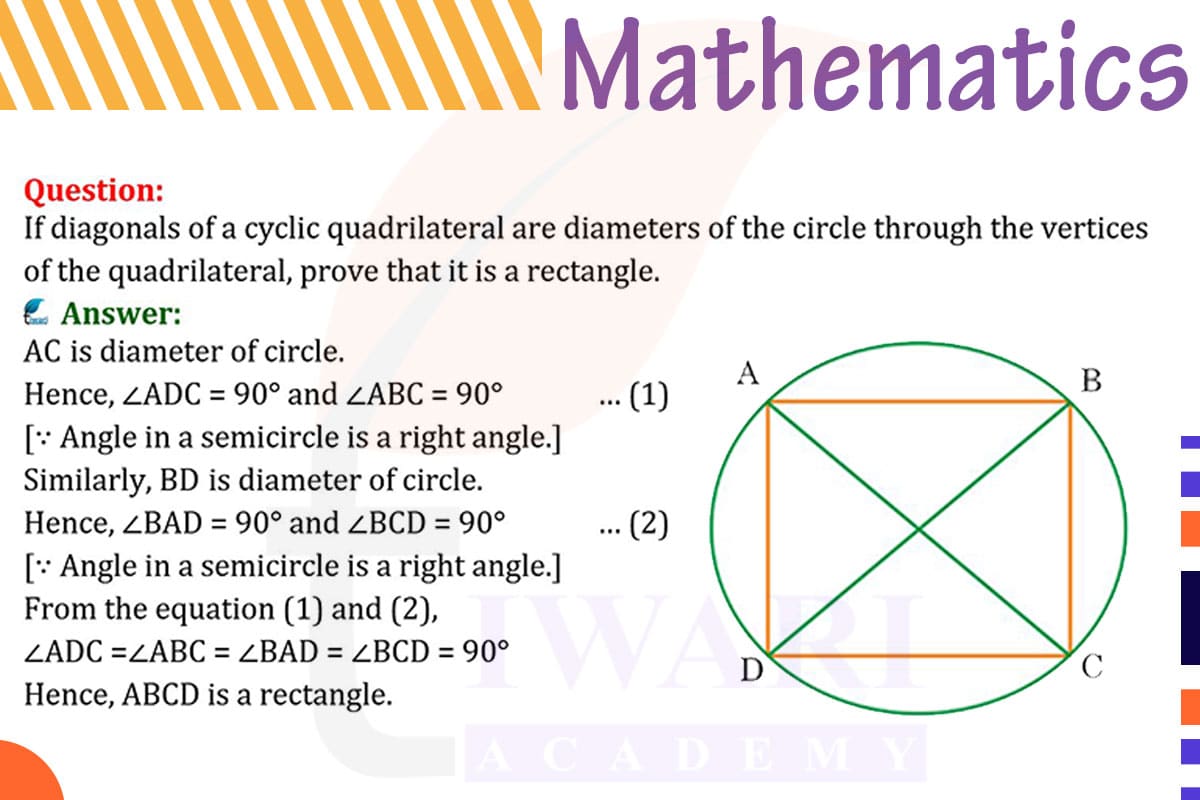
In a cyclic quadrilateral ABCD, if the diagonals AC and BD are diameters of the circle, then each diagonal passes through the center of the circle, making them perpendicular to each other. Since the diagonals of a circle are perpendicular at the center, ∠ADB and ∠BCA are right angles.
In a cyclic quadrilateral, the opposite angles are supplementary. Since ∠ADB and ∠BCA are right angles (90°), their opposite angles ∠ABC and ∠DCB must also be 90° to maintain the supplementary relationship.
Thus, all angles in the quadrilateral are right angles, proving that ABCD is a rectangle.
Let’s discuss in detail
Cyclic Quadrilaterals and Circle Geometry
In the study of geometry, cyclic quadrilaterals present intriguing properties, especially when their diagonals interact with the circles they are inscribed in. A particularly interesting case arises when the diagonals of a cyclic quadrilateral are also the diameters of the circle. This setup leads to a unique geometric configuration, and we are tasked with proving that such a quadrilateral is, in fact, a rectangle. This problem involves applying fundamental concepts of circle geometry and the properties of cyclic quadrilaterals.
The Significance of Diagonals as Diameters
When the diagonals of a quadrilateral are also the diameters of the circle it is inscribed in, they pass through the circle’s center. This is a critical observation because, in a circle, the diameter is the longest possible chord and it bisects the circle into two equal halves. Moreover, any diameter of a circle subtends a right angle to any point on the circle’s circumference. This property is key to understanding the nature of the quadrilateral formed.
Perpendicular Nature of the Diagonals
Given that the diagonals are diameters, they not only pass through the center of the circle but are also perpendicular to each other. This perpendicularity arises from the property of a circle where the diameter subtends a right angle to the circumference. Therefore, at the point where the diagonals intersect, which is the center of the circle, they form right angles with each other.
Implications for the Quadrilateral’s Angles
In any quadrilateral, the angles at which the diagonals intersect are significant. Since in our case the diagonals are perpendicular, the angles formed at their intersection points are right angles (90°). This means that ∠ADB and ∠BCA are right angles. In a cyclic quadrilateral, the opposite angles are supplementary (adding up to 180°). Therefore, if one angle is 90°, its opposite angle must also be 90° to satisfy this condition.
Establishing the Quadrilateral as a Rectangle
With the knowledge that ∠ADB and ∠BCA are right angles, and their opposite angles (∠ABC and ∠DCB) must also be right angles, we can conclude that all angles in the quadrilateral are right angles. A four-sided figure with all right angles is by definition a rectangle. Hence, the cyclic quadrilateral with diagonals as diameters of the circle is proven to be a rectangle.
Geometric Relationships in Cyclic Quadrilaterals
This problem illustrates the elegant relationships and properties within cyclic quadrilaterals and circle geometry. By understanding the implications of diagonals being diameters of a circle, we can deduce the nature of the quadrilateral they form. This exercise not only demonstrates the logical coherence of geometric principles but also highlights the interconnectedness of different geometric concepts, leading to a deeper appreciation of the subject.
Discuss this question in detail or visit to Class 9 Maths Chapter 9 for all questions.
Questions of 9th Maths Exercise 9.3 in Detail

