A triangle ABC is drawn to circumscribe a circle of radius 4 cm

Updated on December 2, 2023
by Tiwari Academy

To find the lengths of sides AB and AC in a triangle ABC circumscribing a circle:
Equal Tangents: Tangents from a common point to a circle are equal. Let the points where the circle touches AB and AC be E and F, respectively.
Segment Lengths: Since BD = 8 cm and DC = 6 cm, by the tangent property, BE = BD = 8 cm and CF = CD = 6 cm.
Finding AB and AC: AB is the sum of tangents from B, so AB = BD + BE = 8 + 8 = 16 cm. Similarly, AC = CD + CF = 6 + 6 = 12 cm.
Therefore, the lengths of sides AB and AC are 16 cm and 12 cm, respectively. This solution utilizes the property of equal tangents from a common external point to a circle.

A triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively.

Let’s discuss in detail

Introduction to the given Question

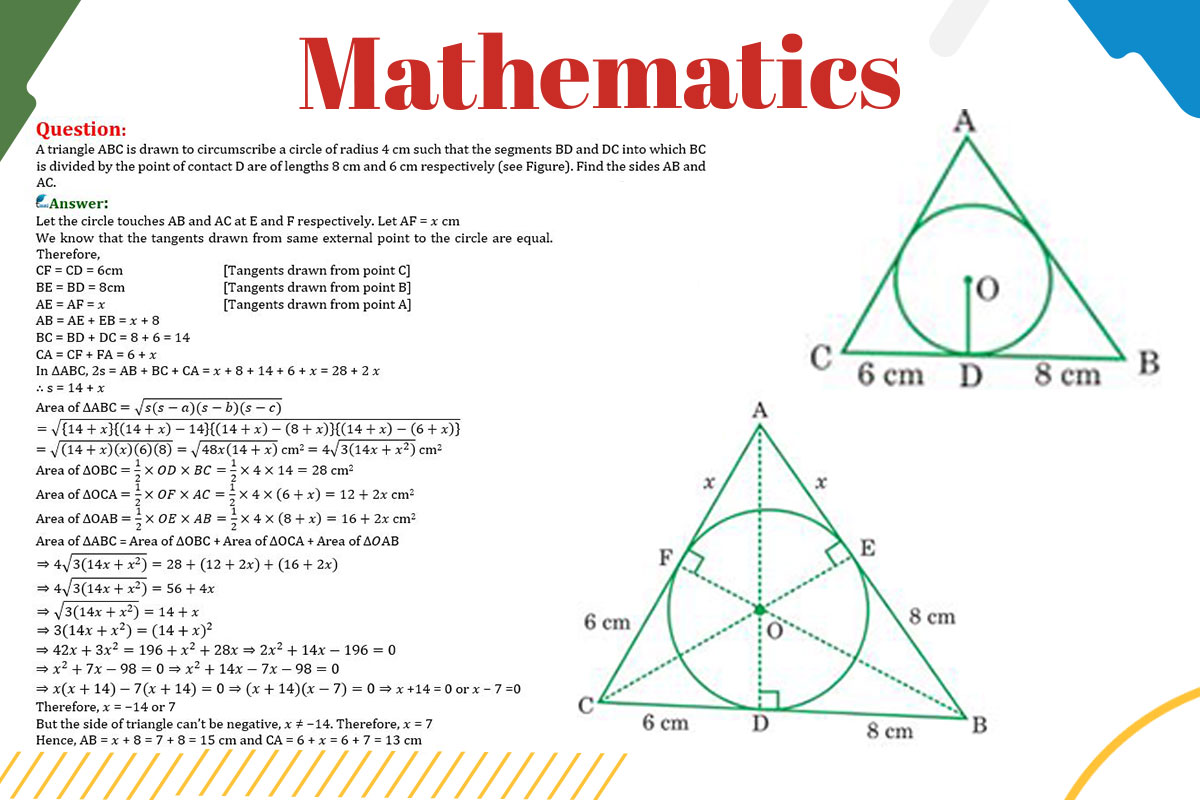
In the study of circle geometry, a common problem involves finding the lengths of sides of a triangle that circumscribes a circle. This problem becomes particularly interesting when specific segments of the triangle, created by the points of tangency, are known. In our case, we have a triangle ABC circumscribing a circle of radius 4 cm, with the segments BD and DC (into which BC is divided by the point of contact D) having lengths of 8 cm and 6 cm, respectively. The objective is to determine the lengths of sides AB and AC.

Understanding Tangents and Circumscribed Circles

A key concept in solving this problem is understanding the properties of tangents to a circle. A tangent is a line that touches a circle at exactly one point. In the context of a circumscribed circle, each side of the circumscribing triangle touches the circle at exactly one point. A fundamental property of tangents from a common external point to a circle is that they are equal in length.

Applying the Tangent Property to Triangle ABC

In triangle ABC, the circle touches sides AB and AC at points E and F, respectively. The tangent property states that segments from a common point to the points of tangency are equal in length. Therefore, BE = BD and CF = CD. Given that BD is 8 cm and CD is 6 cm, we can deduce that BE is also 8 cm and CF is also 6 cm.

Calculating the Length of Side AB
To find the length of side AB, we consider the segments BE and BD. Since BE = BD and BD = 8 cm, the length of BE is also 8 cm. The length of AB is the sum of the lengths of BE and BD, as they both lie on side AB. Therefore, AB = BE + BD = 8 cm + 8 cm = 16 cm.

Calculating the Length of Side AC

Similarly, to find the length of side AC, we look at the segments CF and CD. Since CF = CD and CD = 6 cm, the length of CF is also 6 cm. The length of AC is the sum of the lengths of CF and CD, as they both lie on side AC. Therefore, AC = CF + CD = 6 cm + 6 cm = 12 cm.

Determining the Sides of the Triangle

By applying the properties of tangents to a circumscribed circle, we have successfully determined that the lengths of sides AB and AC in triangle ABC are 16 cm and 12 cm, respectively. This problem illustrates the elegant application of geometric principles to solve problems involving circumscribed figures and tangents, showcasing the logical coherence and beauty of geometry.

Discuss this question in detail or visit to Class 10 Maths Chapter 10 for all questions.
Questions of 10th Maths Exercise 10.2 in Detail

From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is (A) 7 cm (B) 12 cm (C) 15 cm (D) 24.5 cm

If TP and TQ are the two tangents to a circle with centre O so that ∠POQ = 110°, then ∠PTQ is equal to (A) 60° (B) 70° (C) 80° (D) 90°

If tangents PA and PB from a point P to a circle with centre O are inclined to each other at angle of 80°, then ∠POA is equal to (A) 50° (B) 60° (C) 70° (D) 80°

Prove that the tangents drawn at the ends of a diameter of a circle are parallel.

Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.

The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.

Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.

A quadrilateral ABCD is drawn to circumscribe a circle. Prove that AB + CD = AD + BC.

If XY and X’Y’ are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and X’Y’ at B. Prove that ∠AOB = 90°.

Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre.

Prove that the parallelogram circumscribing a circle is a rhombus.