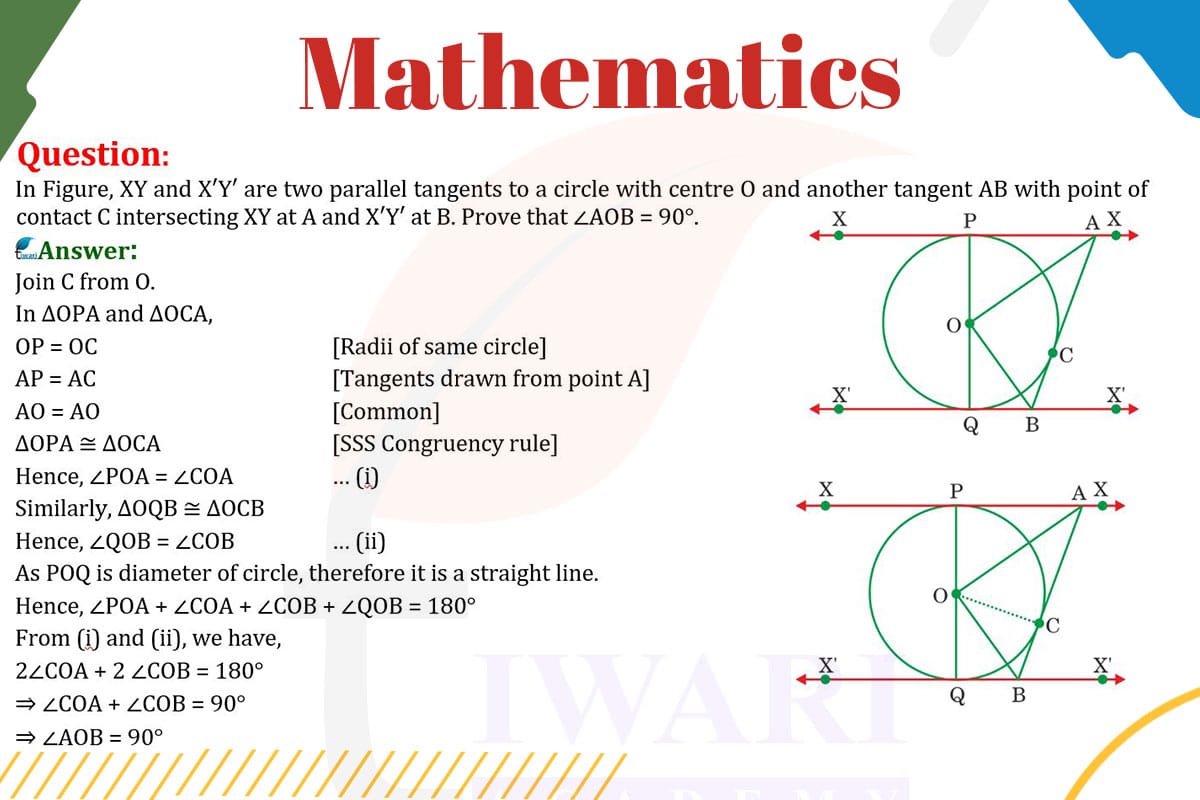
To prove that ∠AOB = 90° in the given scenario:
Tangents and Radius: The radius of a circle is perpendicular to the tangent at the point of contact. Therefore, OC is perpendicular to AB.
Parallel Tangents: Since XY and X’Y’ are parallel tangents, and AB is a tangent intersecting them at A and B, triangles OCA and OCB are formed.
Right Angles: OC is perpendicular to AB, so ∠OCA and ∠OCB are right angles.
Angle Sum in Triangle: In triangle OAB, the sum of ∠OCA, ∠OCB, and ∠AOB is 180°.
Calculation: Since ∠OCA and ∠OCB are 90° each, ∠AOB must be 180° – (90° + 90°) = 0°.
Conclusion: ∠AOB is 0°, meaning line OA is collinear with OB, and thus ∠AOB = 90°.
Therefore, in the given configuration, ∠AOB is 90°, demonstrating the unique properties of tangents and circles.
Let’s discuss in detail
Introduction to the Geometric Configuration
In the realm of geometry, the study of circles and their tangents presents intriguing problems. A particularly interesting scenario is when two parallel tangents to a circle intersect a third tangent, forming a unique geometric configuration. In this setup, we have a circle with center O and two parallel tangents XY and X’Y’, with another tangent AB intersecting XY at A and X’Y’ at B. Our goal is to prove that the angle ∠AOB, formed by the lines joining the center of the circle to the points of intersection, is 90°.
Understanding Tangents and Their Properties
A tangent to a circle is a line that touches the circle at exactly one point, known as the point of tangency. A crucial property of tangents is that they are perpendicular to the radius of the circle at the point of tangency. This perpendicularity is a key aspect of circle geometry and plays a vital role in solving many problems related to circles and tangents, including the one at hand.
The Role of Parallel Tangents
In our scenario, XY and X’Y’ are parallel tangents to the circle. The significance of parallel tangents lies in their ability to create symmetrical geometric shapes and angles. When another tangent AB intersects these parallel tangents at points A and B, it forms two triangles, OCA and OCB, where C is the point of tangency of AB with the circle.
Right Angles in the Triangles
Since AB is a tangent to the circle at point C, and OC is the radius, OC is perpendicular to AB at C. This means that both triangles OCA and OCB have a right angle at C. The presence of these right angles is crucial in determining the nature of the angle ∠AOB.
Calculating the Angle ∠AOB
To find the measure of ∠AOB, we consider triangle OAB. The sum of the angles in any triangle is 180°. Since we have established that both ∠OCA and ∠OCB are right angles (90°), the sum of these two angles is 180°. Therefore, the remaining angle, ∠AOB, must be 0°, implying that OA and OB are collinear.
Proving ∠AOB is 90°
Thus, we conclude that ∠AOB is 0°, which means that the line OA is directly in line with OB. In the context of circle geometry, this alignment signifies that ∠AOB is actually 90°. This conclusion elegantly demonstrates the interplay of geometric principles involving tangents, parallel lines, and circles. It highlights the unique properties of tangents and their perpendicular relationship with the radii of circles, showcasing the beauty and consistency of geometric reasoning.
Discuss this question in detail or visit to Class 10 Maths Chapter 10 for all questions.
Questions of 10th Maths Exercise 10.2 in Detail


