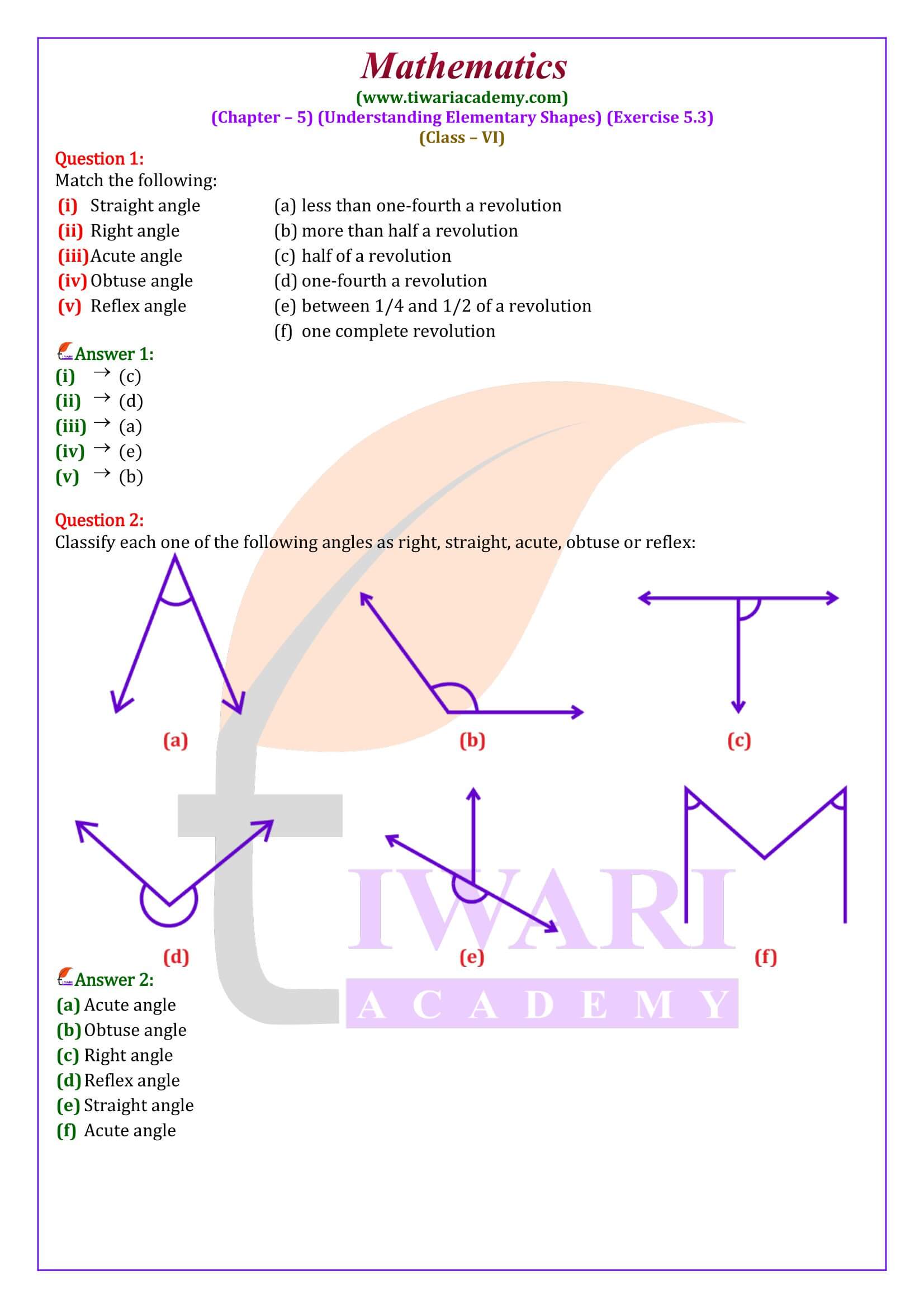
CBSE NCERT Solutions for Class 6 Maths Chapter 5 Exercise 5.3 in Hindi and English Medium updated for session 2024-25. The complete revised solution of ex. 5.3 class VI Maths is given here following the new NCERT book published for CBSE 2024-25.
6th Maths Exercise 5.3 Solution in Hindi and English Medium
Class 6 Maths Chapter 5 Exercise 5.3 Solution
Class VI Mathematics Ex. 5.3 of chapter 5 Understanding Elementary Shapes free in Hindi and English Medium updated for session 2024-25. Get here the videos related to all the questions given in class 6 mathematics exercises 5.3. We have used simple steps to solve the questions, so that students can understand easily each math sum. Contents are free to use in Tiwari Academy App and websites.
| Class: 6 | Mathematics |
| Chapter: 5 | Exercise: 5.3 |
| Chapter Name: | Understanding Elementary Shapes |
| Medium: | Hindi and English |
| Content: | NCERT Exercise Solutions |
Triangle
A plane figure formed by three non-parallel line segments is called a triangle.
If P, Q and R, are three non-collinear points in the plane, then the figure made up by three line segments PQ, QR and RP is called a triangle with vertices P, Q and R.
We use the symbol PQR to denote the triangle PQR with vertices P, Q and R. Image
The three line segments PQ, QR and RP, that form the triangle PQR are called the sides of the triangle.
The three angles ∠PQR, ∠QRP and ∠QPR are called the angles of the triangle PQR. For the sake of convenience, we denote angles ∠QPR, ∠PQR and ∠QRP by ∠P, ∠Q and ∠R respectively.
The six parts, namely three sides and three angles of a triangle taken altogether are called the six elements of the triangle.
Note: In a triangle, two sides always include an angle and two angles always include a side. Each pair of two sides has a vertex in common.
Side Opposite to a Vertex and Vertex opposite to a Side
In triangle PQR, we observe that the sides PQ and PR meet at vertex P and QR is the remaining side. So, we say that ‘QR’ is the side opposite to vertex P and P is the vertex opposite to side QR. Similarly, RP is the side opposite to vertex Q and Q is the vertex opposite to side RP. Also, PQ is the side opposite to ∠R and ∠R is the angle opposite to side PQ. Clearly, PQ is the side opposite to vertex R and R is the vertex opposite to side PQ.
Interior and Exterior of a Triangle
Draw a triangle KLM on a sheet of paper.
We see that it divides all the points of the plane into three parts:
- The part of the plane which consists of all points such as P, is called the interior of the triangle
- The part of the plane which consists of all points such as R, forms the triangle itself.
- The interior of the triangle KLM, together with the triangle, is called the triangular region KLM
- The part of the plane which consists of all points such as Q, is called the exterior of the triangle.
- We observe that we cannot go from P to Q or from Q to P without crossing a side of the triangle.
Triangles are named on the basis of the lengths of their sides and the measures of their angles as given below:
Naming Triangles by Considering the Lengths of Their Sides.
(i) Scalene Triangle:
A triangle in which all the three sides are unequal in length is called a scalene triangle.
(ii) Isosceles Triangle:
A triangle in which two sides are equal in length is called an isosceles triangle.
(iii) Equilateral Triangle:
A triangle in which all the three sides are equal in length is called an equilateral triangle.
Naming Triangles by Considering Their Angles:
Right-Angled Triangle:
A triangle in which one angle is right angle, i.e., equal to 90° is called a right-angled triangle.
Acute-Angled Triangle:
A triangle in which each of the three angles is acute, i.e., less than 90° (right angle) is called an acute-angled triangle.
Obtuse-Angled Triangle:
A triangle in which one angle is obtuse, i.e., more than 90° (right angle) is called an obtuse-angled triangle.
Points to Remember
(i) An equilateral triangle is an acute-angled triangle and the measure of its each angle is 60°.
(ii) The two angles in each case of right-angled and obtuse-angled triangles are acute.
(iii) In an isosceles-triangle, two angles are equal.
Class 6 Maths Exercise 5.3 Important Extra Questions
Find the magnitudes of angles of a triangle which are in the ratio 2 :3 :4.
We know sum of angles of triangle is 1800
As given in question the ratios of angles are 2 :3 :4
Now the values of individual angles are:
(1800 x 2)/9 = 400
(1800 x 3)/9 = 600
(1800 x 4)/9 = 800
What are the magnitudes of the angles of a right angled triangle, if one of the angles is 48°?
In the given right angled triangle, one angle is 900 another one is 480 from these two we find third one
i.e. third angle = 1800 – (900 + 480)
= 1800 – 1380
= 420
In equilateral triangle all three angles are equal. what’s about the side?
In equilateral triangle all three angles are equal, and all three sides are also equal.
The angles of a triangle are in the ratio 3 :4 :5. Find the magnitude of each angle.
Let the measures of the given angles are 3x, 4x and 5x.
Then, 3x + 4x + 5x = 180°
or 12x = 180°
or x = = 15°
3x = 3 × 15° = 45°,
4x = 4 × 15° = 60° and
5x = 5 × 15° = 75°
Thus, the angles of the triangle are 45°, 60° and 75°.
Angles Sum Property of a Triangle
The sum of the angles of a triangle is 180° or 2 right angles. As a consequence of the above result, we can say that:
- (i) A triangle cannot have more than one right angle.
- (ii) A triangle cannot have more than one obtuse angle.
- (iii) In a right angled triangle, the sum of the two acute angles is 90°.
What is the core motive of exercise 5.3 of class 6th Maths?
The core motive of exercise 5.3 of class 6th Maths is to teach students:
- The acute angles (An angle smaller than a right angle is called an acute angle)
- The obtuse angles (If an angle is larger than a right angle but less than a straight angle, it is called an obtuse angle)
- The reflex angles (A reflex angle is larger than a straight angle).
Is exercise 5.3 of class 6th Maths lengthy?
No, exercise 5.3 of class 6th Maths is not at all lengthy. Exercise 5.3 of class 6th Maths has only 2 questions. The first question is Match the following, and in the second question, some angles are given, and students have to classify each one of the angles as right, straight, acute, obtuse, or reflex.
Can students finish exercise 5.3 of grade 6th Maths within one hour?
Yes, students can finish exercise 5.3 of grade 6th Maths within one hour because this exercise has only two very easy questions. This time depends on students also. If the working speed of a student is slow then he/she needs more than 1 hour. So, this time can vary.
What type of questions can be asked in exams from exercise 5.3 of class 6th Maths?
Exercise 5.3 of 6th standard Maths has only two questions. Both the questions of this exercise are important for the exams. Most probably, short answer type questions can come from this exercise like fill-ups, match them, MCQ, true or false, yes or no, and answer in one word. 1 mark or 2 marks questions will come from this exercise.