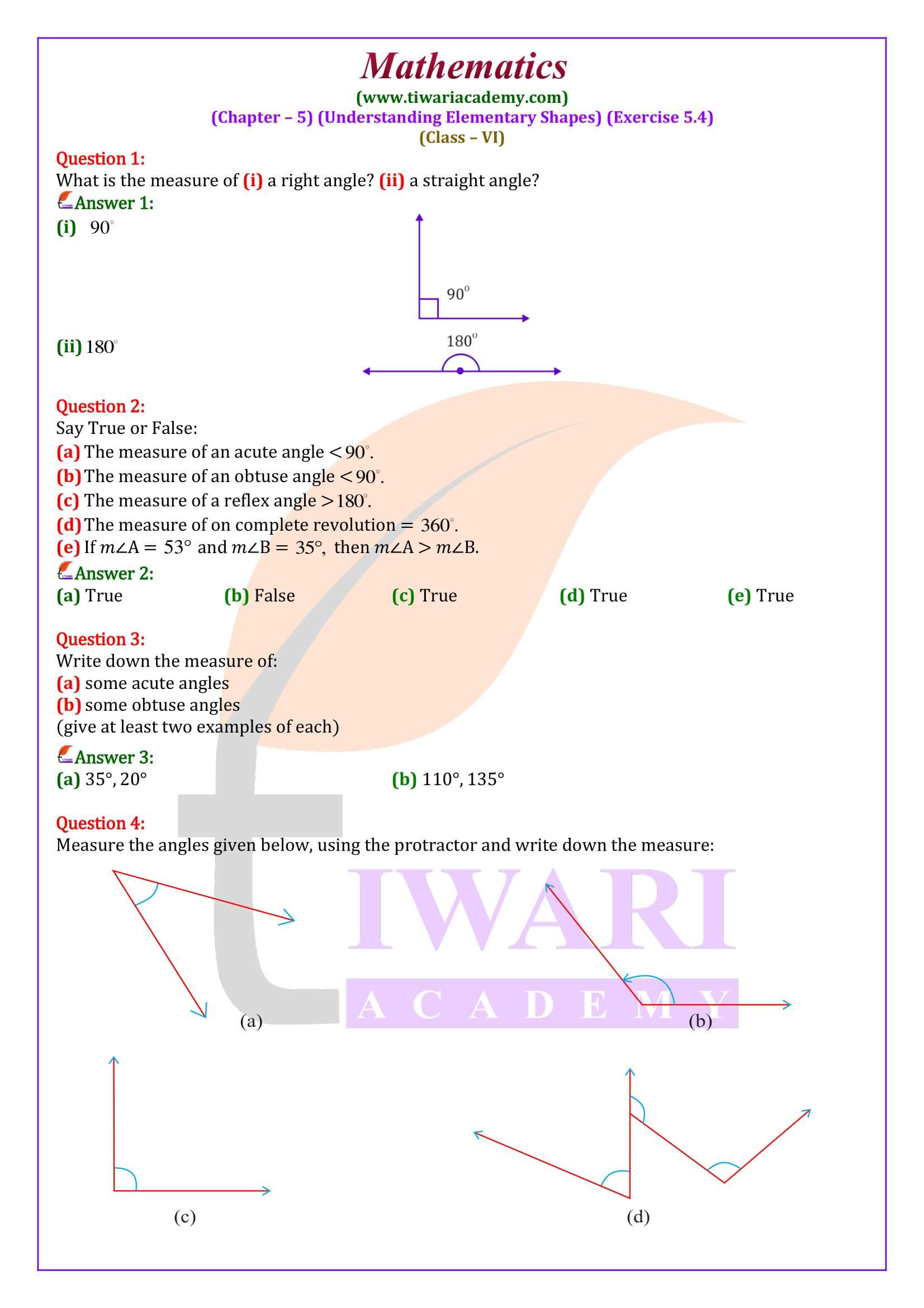
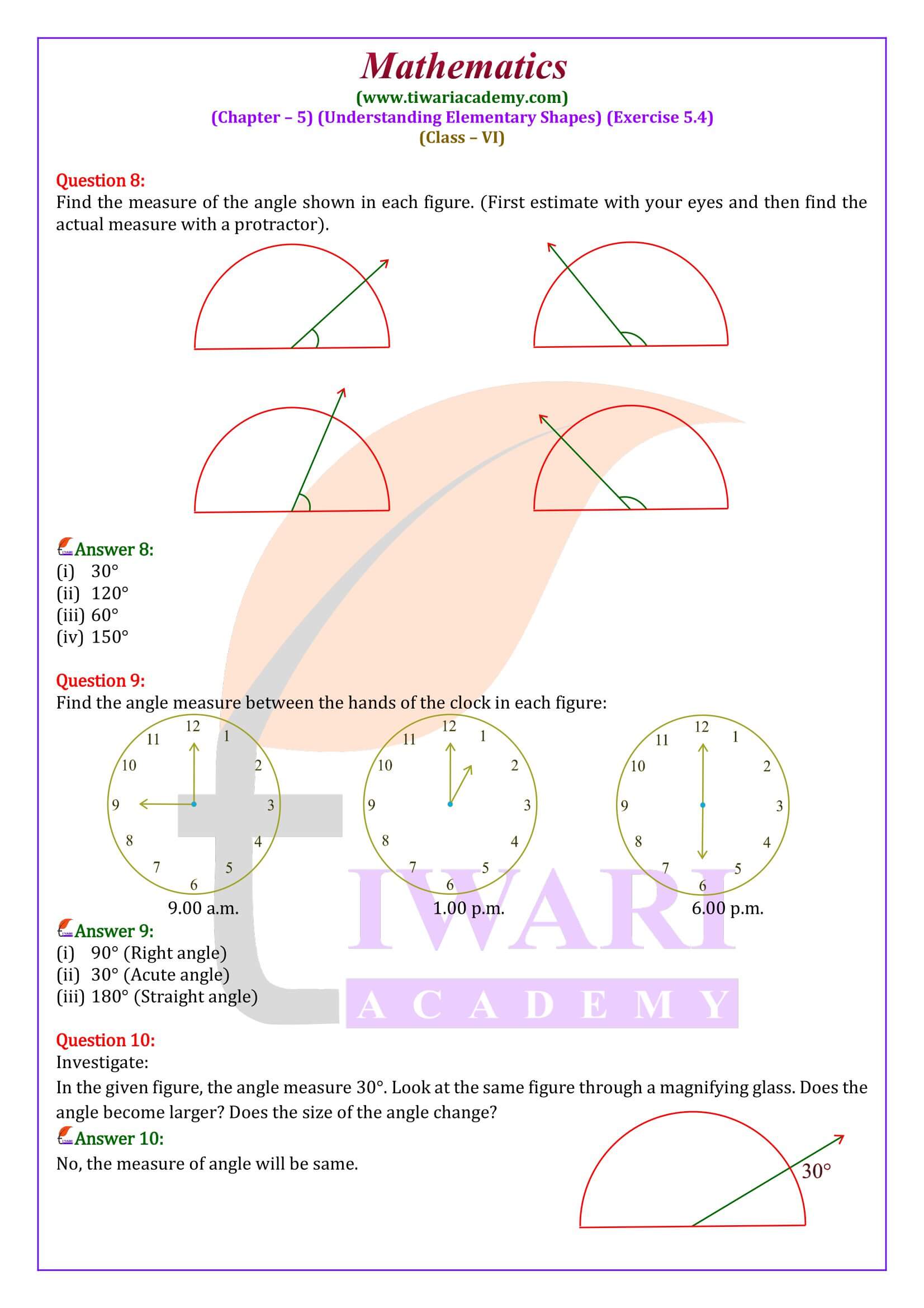
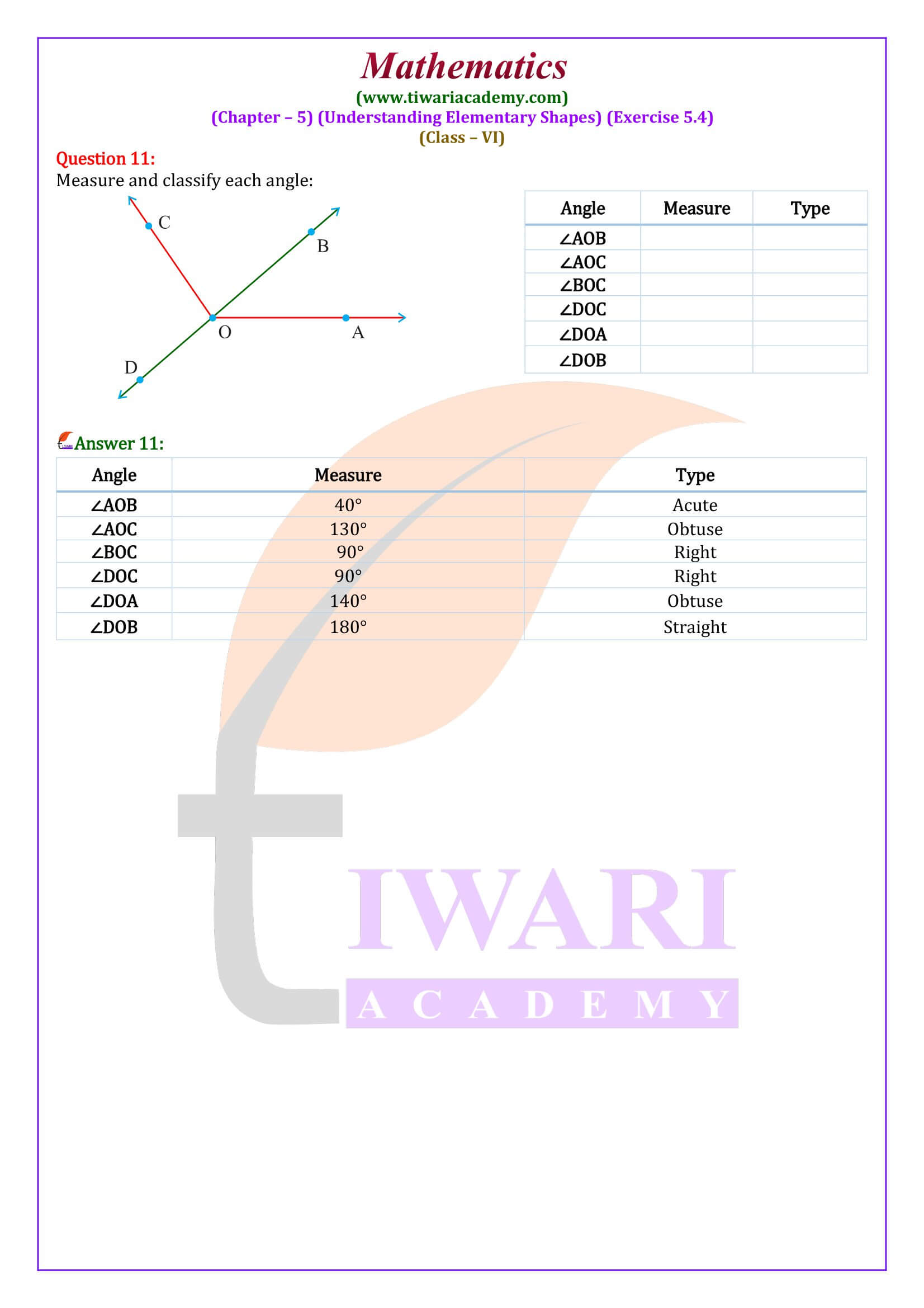
CBSE NCERT Solutions for Class 6 Maths Chapter 5 Exercise 5.4 in Hindi and English Medium for new session 2025-26. We have updated the solutions of ex. 5.4 class VI Maths following the rationalised syllabus and new NCERT textbooks issued for CBSE 2025-26 curriculum.
6th Maths Exercise 5.4 Solution in Hindi and English Medium
Class 6 Maths Chapter 5 Exercise 5.4 Solution
Class VI Mathematics NCERT textbook Ex. 5.4 of chapter 5 Understanding Elementary Shapes in Hindi and English Medium free to download. 6th NCERT Books PDF and Videos are updated for academic session 2025-26 free to download. If students are feeling difficulties to use the solutions, contact us immediately for help. We are here to help you without any charge. Our main motive is to help the students and make the study stress-free.
| Class: 6 | Mathematics |
| Chapter: 5 | Exercise: 5.4 |
| Chapter Name: | Understanding Elementary Shapes |
| Medium: | Hindi and English Medium |
| Content: | NCERT Exercise Solutions |
Circle
A circle is a closed plane figure consisting of all those points of the plane which are at a constant distance from a fixed point.
The fixed point is called the centre of the circle and the constant distance is known as the radius of the circle.
If O is the centre of the circle and OM = r is the radius of the circle.
If N is another point on the circle, then the line segment ON is another radius of the circle. All the radii of the circle have one end point common, which is the centre of the circle. Also, OM = ON = r.
Thus, all radii of a circle are equal.
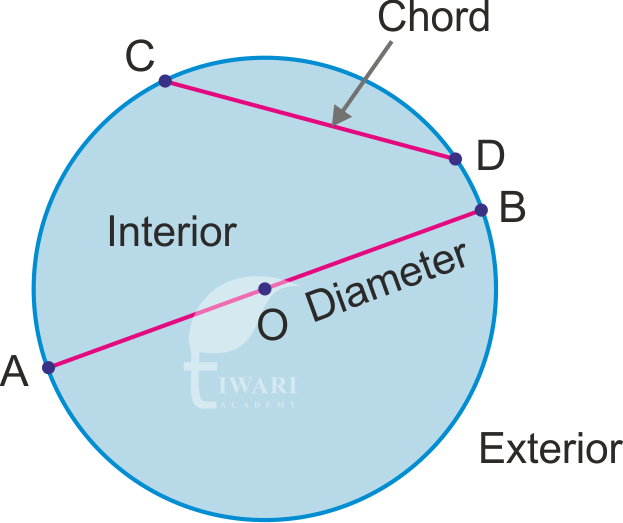
Diameter of Circle:
A line segment passing through the centre of a circle and having its end points on the circle, is called diameter of the circle.
If, PQ is a diameter of the circle having its centre at O. Also, OP and OQ are two radii of the circle.
So OP = OQ, because O is the mid-point of PQ.
Thus, the centre of a circle bisects a diameter into two equal parts.
Hence, Diameter = 2 × Radius
Just as we can draw an infinite number of radii through the centre of a circle, we can draw an infinite number of diameters.
As observed earlier, the centre O of a circle is the mid-point of every diameter of circle. Thus, the diameters of a circle are concurrent and the common point is the centre of the circle.
Interior and Exterior of a Circle
Consider a circle with centre O and radius r. This circle divides the plane into three parts:
- The part of the plane, consisting of those points P, for which OP < r, is called the interior of the circle, with centre O and radius r. In other words, the set of all those points which lie inside the circle is known as its interior.
- The part of the plane, consisting of those points P for which OP > r, is called the exterior of the circle, with centre O and radius r. In other words, the set of all those points which lie outside the circle is called the exterior of the circle.
- The part of the plane, consisting of those points P, for which OP = r, is the circle itself, i.e., the set of all points lying on the circle is the circle itself.
Class 6 Maths Exercise 5.4 Important Extra Questions
Find the diameter of a circle whose radius is: (i) 7 cm (ii) 4.5 cm
Diameter of circle = 2 x radius of circle
(i) Diameter of circle = 2 x 7 = 14 cm
(ii) Diameter of circle = 2 x 4.5 = 9 cm
Find the radius of a circle whose diameter is: (i) 6 cm (ii) 9.2 cm
Radius of a circle = diameter / 2
(i) Radius of a circle = 6 / 2 = 3 cm
(ii) Radius of a circle = 9.2 / 2 = 4.6 cm
How many radii of a circle can be?
Every circle has an infinite number of radii. This is because the number of points on the circumference of the circle is infinite. So there can be an infinite number of lines joining them to the center.
The longest chord of a circle is called.
A chord that passes through the center of a circle is called a diameter and is the longest chord.
What do mean by circumference of a circle?
The perimeter of a circle, often called the circumference, is proportional to its diameter and its radius.
Note: Clearly, the circle, its interior and exterior have no common point and together account for all points of the plane.
The part of the plane of the circle that consists of the circle and its interior is called the circular region.
How many questions are there in exercise 5.4 of class 6th Maths?
Exercise 5.4 of class 6th Maths has 11 questions and no example. All questions of this exercise are important. Students should practice all questions of this exercise. But, some questions of this exercise are most important which students can’t skip for the exams. These questions are 2, 5, 7, 9, and 11.
In how many days, students finish exercise 5.4 of class 6th Maths?
Students finish exercise 5.4 of grade 6th Maths in 3 days if they give 1 hour per day to this exercise. This time can vary because no students can have the same working speed, ability, efficiency, etc.
Is exercise 5.4 of 6th Maths complicated?
If concepts of angles (Acute angle, Obtuse angle, Right angle, Straight angle, Reflex angle, Complete angle) and how to measure angles using protractor is clear to students then, exercise 5.4 of class 6th Maths is easy otherwise complicated.
Which questions of exercise 5.4 of class 6 Maths are best for class test?
Exercise 5.4 of class 6th Maths has 11 questions and no example. Questions 4, 7, 8, and 11 are the best questions of exercise 5.4 of class 6th Maths.