NCERT Solutions for Class 6 Maths Chapter 7 Exercise 7.3 in English and Hindi Medium updated for CBSE 2024-25 exams. Class 6 math ex. 7.3 solutions are revised on the basis of new syllabus and latest NCERT book issued for academic session 2024-25.
6th Maths Exercise 7.3 Solutions in Hindi and English Medium
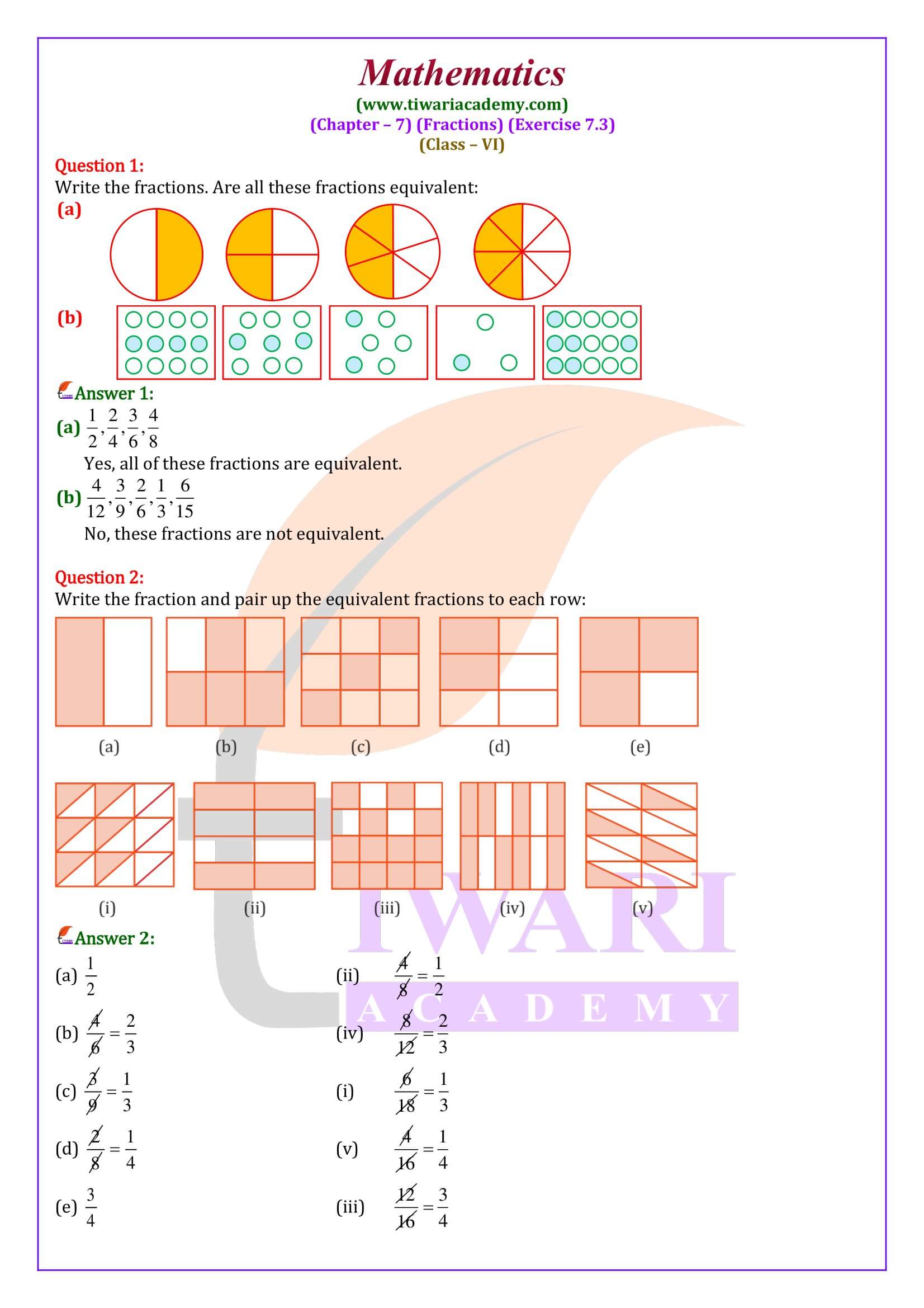
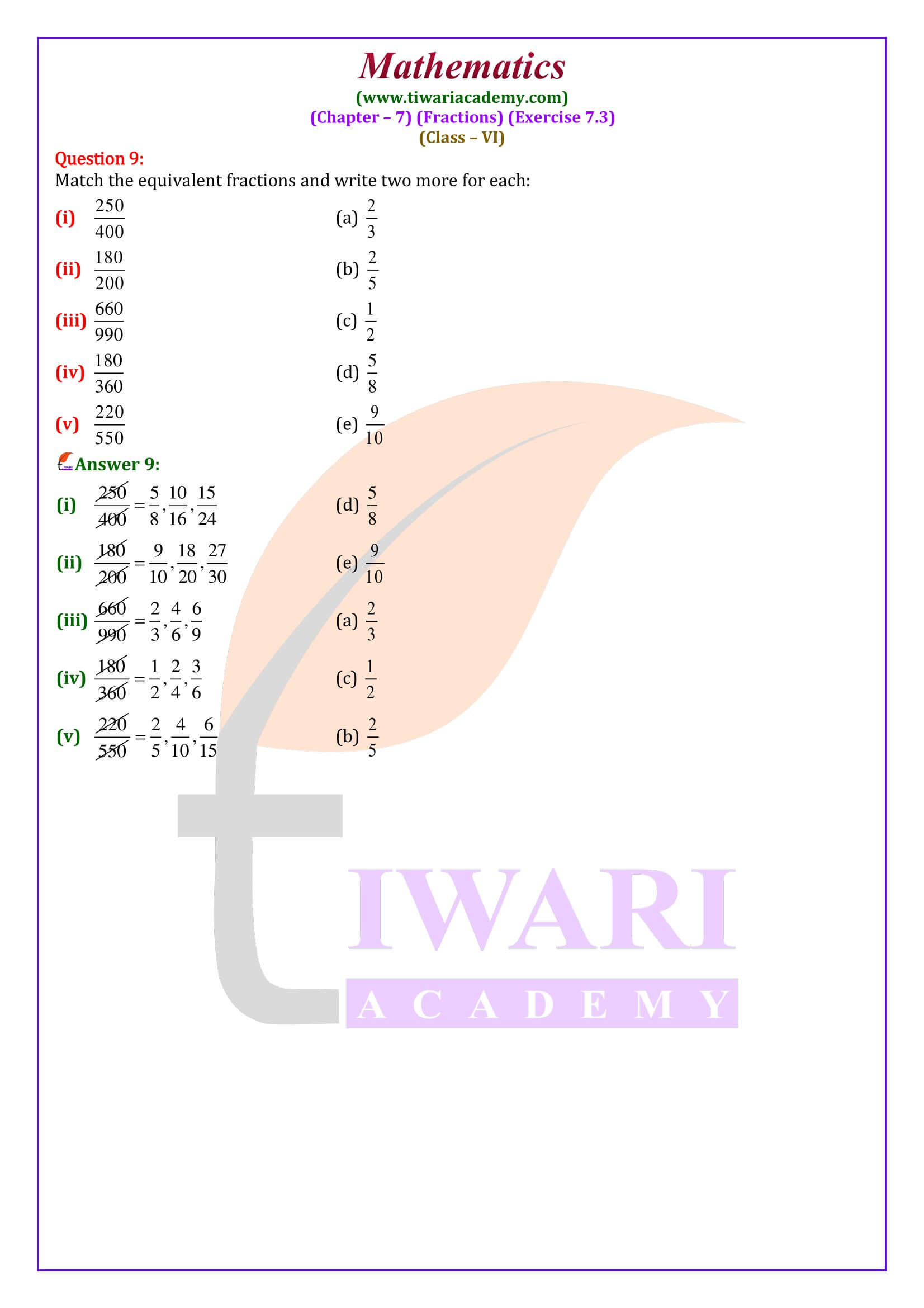
Class 6 Maths Chapter 7 Exercise 7.3 Solution
Class VI Mathematics NCERT (https://ncert.nic.in/) Textbook Ex. 7.3 of chapter 7 Fractions updated for CBSE academic session 2024-25 Hindi and English Medium free. All the contents are designed according to latest CBSE Syllabus for CBSE and state Board students. Class 6 NCERT Book mathematics exercise 7.3 is based on comparison of fractions. PDF solutions and videos help the students to clear their doubts. Practice all the questions and use solutions if any doubt occurs.
| Class: 6 | Mathematics |
| Chapter: 7 | Exercise: 7.3 |
| Chapter Name: | Fractions |
| Medium: | Hindi and English |
| Session: | CBSE Board 2024-25 |
| Content Type: | Text and Online Videos |
Unit Fractions:
A fraction having 1 as numerator is called a unit fractions.
For example, 1/5, 1/8, 1/20, 1/23, 1/12 etc. are all unit fractions.
Proper Fractions:
A fraction having numerator less than its denominator is called a proper fraction.
For example, 2/5, 8/13, 7/15, 4/23 etc. are all proper fractions.
Improper Fractions:
A fraction having numerator greater than its denominator is called an Improper Fraction.
For example, 17/8, 25/13, 37/30, 18/14 etc. are all improper fractions.
Mixed Fractions
A combination of a whole number and a proper fraction is called a mixed fraction
For example, 1(3/4), 4(2/3), 6(5/7) etc. are all mixed fractions.
In 1(3/4), and 4(2/3), 1 and 4 are whole numbers and ¾ and 2/3 are proper fractions.
Class 6 Maths Exercise 7.3 Extra Question with Answer
Convert each of the following mixed fractions into improper fractions: (i) 4(2/5), (ii) 3(1/5), (iii) 6(4/7)
Convert each of the following mixed fractions into improper fractions:
(i) 4(2/5), (ii) 3(1/5), (iii) 6(4/7)
(i) 4(2/5) = {(4 x 5) + 2}/5 = 22/5
(ii) 3(1/5) = {(3 x 5) + 1}/5 = 16/5
(iii) 6(4/7) = {(6 x 7) + 4}/5 = 46/7
Convert each of the following into a mixed fraction: (i) 15/7, (ii) 23/14, (iii) 47/9
(i) On dividing 15 by 7, we get the quotient = 2 and the remainder = 1.
So, 15/7 = 2(1/7)
On dividing 23 by 14, we get the quotient = 1 and the remainder = 9.
So, 23/14 = 1(9/14)
(iii) On dividing 47 by 9, we get the quotient = 5 and the remainder = 2.
So, 47/9 = 5(2/9)
Conversion of Mixed Fractions into Improper Fractions and Vice-Versa
To convert a mixed fraction into an improper fraction, we take the following steps:
Step-1: In the given mixed fraction, identify the whole number, the numerator and the numerator and the denominator of the proper fraction.
Step-2: Multiply the whole number by the denominator of the proper fraction and add the result to the numerator of the proper fraction.
Step-3: Write the fraction having numerator equal to the number obtained in step 2 and denominator same as the denominator of the fraction in step 1. Thus,
Improper fraction = {(Whole number × Denominator) + Numerator} / Denominator
Class 6 Maths Exercise 7.3 Important Questions
What is proper fraction?
A fraction in which the numerator is less or of lower degree than the denominator.
What are the 7 types of fractions?
The six kinds of fractions are, proper fractions, improper fractions, mixed fractions, like fractions, unlike fractions and equivalent fractions.
How do you express fractions in words?
To express the fraction in words, write the numerator, add a hyphen and then spell out the denominator. In word form, the fraction 3/10 would be spelled out as three-tenths.
To convert an improper fraction into a mixed fraction, we follow the following steps:
Step-1: Divide the numerator by the denominator and obtain the quotient and the remainder.
Step-2: Write the mixed fraction as: Quotient (Remainder/Denominator).
What are the main topics that students will study in class 6 Maths Exercise 7.3?
The main topics that students will study in exercise 7.3 of class 6th Maths are:
1. Equivalent fractions
2. The simplest form of a fraction (A fraction is said to be in the simplest (or lowest) form if its numerator and denominator have no common factor except 1).
Does exercise 7.3 of grade 6th Maths has any important example?
Yes, exercise 7.3 of grade 6th Maths has three examples (examples 3, 4, and 5). All examples are quite easy. In all three examples students have to find the equivalent fraction of the given fraction. Examples 3, 4, 5, and questions 4, 5 are of the same type.
Which questions of exercise 7.3 of grade 6th Maths can have a maximum chance to come in the terminal exams?
Exercise 7.3 of grade 6th Maths has 3 examples and 9 questions. The most important problems of this exercise that have a chance to come in the terminal exams are questions 2, 3, 4, 6, 7, and 8.
How much time, students need to solve exercise 7.3 of grade 6th Maths?
Students need a maximum of 2 days to finish exercise 7.3 of grade 6th Maths if they give 1 hour per day to this exercise because this exercise has 3 examples and 9 questions. This time is not fixed and can vary also.