NCERT Solutions for Class 6 Maths Chapter 7 Exercise 7.5 in English and Hindi Medium updated for CBSE session 2025-26. Get the complete revised solutions of ex. 7.5 class 6th Maths based on rationalised syllabus and new NCERT textbook issued for CBSE 2025-26 exams.
6th Maths Exercise 7.5 Solution in Hindi and English Medium
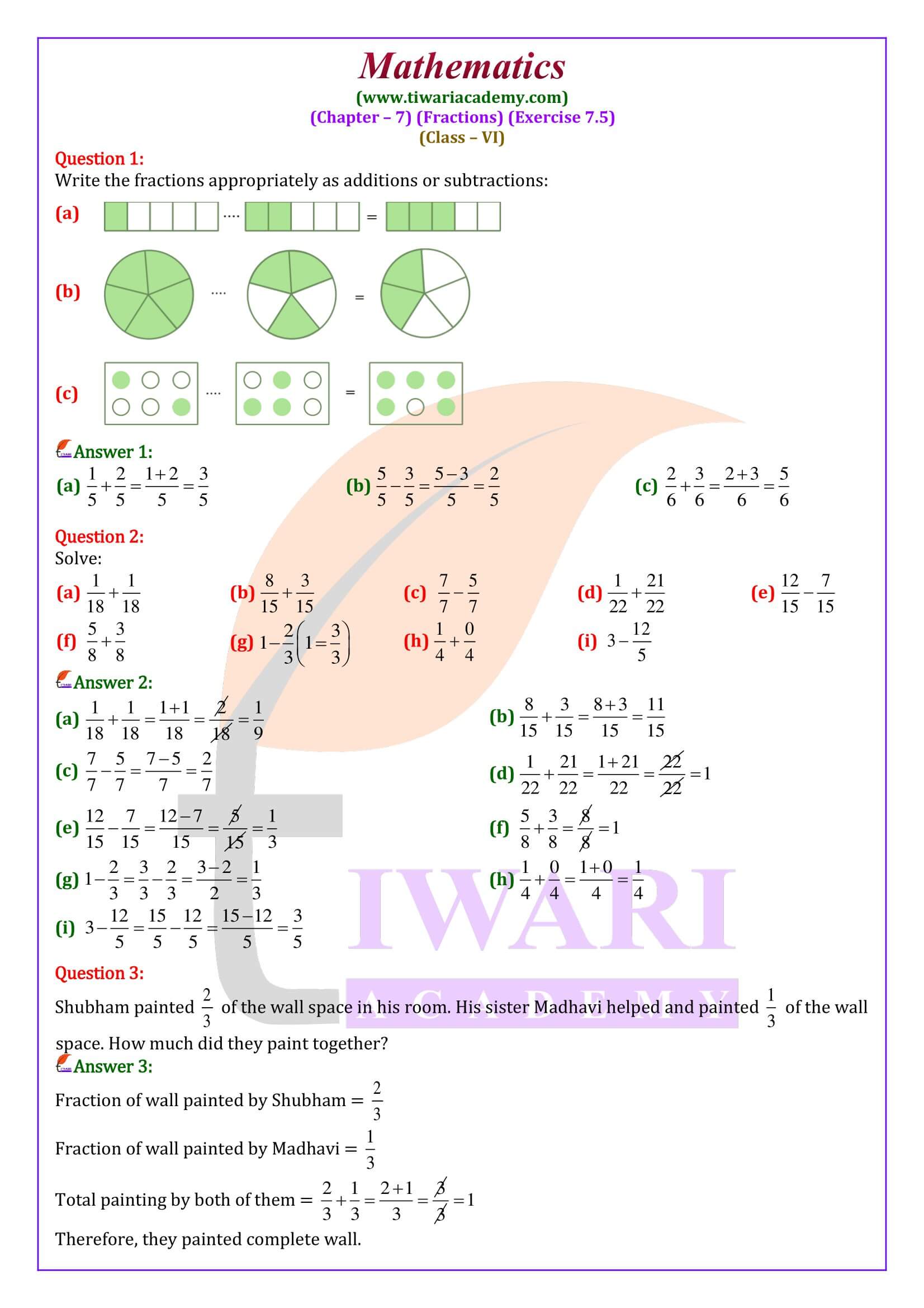
Class 6 Maths Chapter 7 Exercise 7.5 Solution
Class VI Mathematics Ex. 7.5 of chapter 7 Fractions all question answers free to use online or download in PDF file format. All the contents are updated according to latest CBSE Syllabus 2025-26. In exercise 7.5 of class 8 Maths NCERT, questions are based on addition subtraction of simple fractions with some word problems. Take help from videos solution, if someone face difficulty to understand in NCERT textbook PDF question answers.
| Class: 6 | Mathematics |
| Chapter: 7 | Exercise: 7.5 |
| Chapter Name: | Fractions |
| Content Type: | Text and Video Solutions |
| Session: | Academic Year 2025-26 |
| Medium: | Dual Language – Hindi and English |
Comparing Like Fractions
Examples:
(i) 4/9 < 7/9 or 7/9 > 4/9
(ii) 17/19 > 12/19 or 12/19 < 17/19
We have also learnt that three or more like fractions can be arranged in ascending or descending order by arranging their numerators in ascending or descending order.
For example, the fractions
7/10, 1/10, 4/10, 3/10 can be arranged in the ascending order as 1/10 < 3/10 < 4/10 < 7/10
Similarly, the fractions
5/17, 2/17, 6/17, 9/17 can be arranged in the descending order as 9/17 > 6/17 > 5/17 > 2/17
Out of two fractions with the same numerator, the one with smaller denominator is greater of the two.
Examples:
- (i) 4/7 > 4/10
- (ii) 2/3 > 2/5
- (iii) 10/13 > 10/15
For comparing two unlike fractions we have the following rule.
To compare two unlike fractions, we convert them into equivalent fractions by finding LCM of their denominators. Then the fractions having the larger numerator is larger than the one having the smaller numerator.
Alternative Method of Comparing Two Fractions
Let a/b and c/d be the two given fractions. To compare these fractions, we cross multiply, as shown:
Then we find the cross products ad and bc.
(i) If ad > bc then a/b > c/d.
(ii) If ad < bc then a/b < c/d.
(iii) If ad = bc then a/b = c/d.
Class 6 Maths Exercise 7.5 Important Questions
What is the meaning of unlike fraction?
Unlike fractions are fractions that have different denominators. Examples. The first fraction below has a denominator of two and the second fraction below has a denominator of three. Since the denominators are different, they are unlike fractions.
Compare the fractions 2/5 and 3/8.
The LCM of denominators 5 and 8 is 40
Therefore, we convert 2/5 and 3/8 into like fractions each having denominator 40.
2/5 = (2 x 8)/(5 x 8) = 16/40
And 3/8 = (3 x 5)/ (8 x 5) = 15/40
Now, 16/40 and 15/40 are like fractions.
Clearly, 16 > 15
So, 16/40 > 15/40
How do you find unlike fractions?
If the denominators are not the same, then you have to use equivalent fractions which do have a common denominator. To do this, you need to find the least common multiple (LCM) of the two denominators. To add fractions with unlike denominators, rename the fractions with a common denominator. Then add and simplify.
How do you add and subtract unlike fractions?
When the Denominators Are Unlike or Different
When all denominators are alike, simply add or subtract the numerators and place the result over the common denominator. The resulting fraction can be simplified to lowest terms or written as a mixed number.
Compare the fractions 5/9 and 6/13.
By cross multiplying, we get:
5 × 13 = 65 and 9 × 6 = 54
Clearly, 65 > 54
Hence, 5/9 > 6/13
Can short answer-type questions come in the exam from class 6 Maths Exercise 7.5?
Yes, Exercise 7.5 of class 6th Maths contains five questions. Fill in the blanks, true or false (yes or no), one-word answer, MCQ, match them type questions can come from exercise 7.5 of class 6th Maths in the exam. One mark and two marks questions can come from this exercise.
Which questions are important questions of exercise 7.5 (class 6th Maths)?
There are five questions and no examples in exercise 7.5 of class 6th Maths. All the questions of this exercise are important for the exams. Students should practice all the questions of this exercise for exams. But, the most important questions of this exercise which have more chance than other questions of this exercise to come in the exams are questions 4 and 5.
Can students complete exercise 7.5 of class 6 Maths in 2-3 hours?
Students can complete exercise 7.5 of class 6th Maths in 2-3 hours or not depends on student’s working speed, efficiency, capability, and many other factors. But if they honestly and seriously try to complete exercise 7.5 of class 6th Maths in 2-3 hours, they can easily do that because exercise 7.5 has only five questions.
Is exercise 7.5 of class 6th Maths easy to solve?
Yes, exercise 7.5 of class 6th Maths is very easy to solve. In this exercise students study topic “Adding or subtracting like fractions”. Exercise 7.5 of class 6th Maths contains straightforward and good questions.