NCERT Exercise Solutions for Class 12 Mathematics Chapter 4 Determinants, play a crucial role in mastering the fundamental concepts of determinants. NCERT Class 12th Mathematics solutions cover all exercises, including Exercise 4.1 and NCERT Exercise 4.2, in a step-by-step manner. Determinants help solve systems of linear equations and are widely used in various branches of mathematics, including algebra and calculus. By practicing these NCERT PDF Solutions for Class 12 Maths Chapter 4, students can strengthen their understanding of topics like properties of determinants, minors, and cofactors. NCERT Textbook solutions for the Miscellaneous Exercise Chapter 4 offer advanced practice, ensuring students are well-prepared for board exams.
NCERT Textbook Solutions for Class 12 Maths Chapter 4 Determinants
Whether working on Exercise 4.3 or solving complex problems in Exercise 4.6, students can rely on NCERT Simple Solutions for a structured approach. The solutions are available in PDF format, making them accessible for quick revisions before exams. NCERT Revised Solutions for class 12 Maths chapter 4 Determinants all exercise with miscellaneous in Hindi and English Medium new session 2025-26. The questions of each exercise is changed as per the new syllabus for CBSE 2025-26.
Key Features of Class 12 Mathematics Determinants NCERT Textbook Solutions
Class 12th Mathematics Determinants NCERT Detailed Solutions are designed to help students develop problem-solving skills with clear explanations. NCERT Exercise 4.4 introduces the application of determinants in real-life scenarios, such as calculating areas of triangles and verifying collinearity. Similarly, NCERT Book Exercise 4.5 focuses on determinants of matrices and their role in finding the inverse of a matrix. Class 12 NCERT Mathematics Book solutions emphasize the properties of determinants, ensuring students grasp key concepts easily.
NCERT Class 12th Math Textbook Chapter 4 solutions are comprehensive and include detailed methods for solving problems, making them ideal for both beginners and advanced learners. The Miscellaneous Exercise Chapter 4 offers challenging problems to test overall understanding. Downloading the PDF solutions for Class 12 Mathematics Chapter 4 allows students to study offline at their convenience. Practicing these solutions regularly builds confidence in tackling determinant-based questions in exams.
Important Points for Class 12 Maths Chapter 4 Determinants
Key points for exams include the properties of determinants, calculation of minors and cofactors, adjoint and inverse of matrices and solving linear equations using determinants. Focus on NCERT exercises like 4.3, 4.5 and the Miscellaneous Exercise for advanced problems. Practice applications in geometry, such as collinearity and area of triangles.
| Day | Topics to Cover | Exercises to Practice | Notes/Highlights |
|---|---|---|---|
| Day 1 | Introduction to Determinants, Properties of Determinants | Exercise 4.1 | Focus on understanding properties and simple problems. |
| Day 2 | Minors and Cofactors | Exercise 4.2 | Practice cofactor expansions and simplify expressions. |
| Day 3 | Adjoint and Inverse of a Matrix | Exercise 4.3 | Learn the formula and practice finding the inverse of matrices. |
| Day 4 | Applications of Determinants in Geometry | Exercise 4.4 | Focus on area of triangles and verifying collinearity. |
| Day 5 | Miscellaneous Problems | Miscellaneous Exercise | Attempt higher-level problems to strengthen concepts. |
| Day 6 | Revision of All Topics | Key Examples and Selected Questions | Summarize formulas, revisit mistakes and clear doubts. |

Benefits of Solving NCERT Class 12 Mathematics Chapter 4 Exercises
Solving NCERT Textbook Class 12 Maths Chapter 4 exercises is essential for students aiming to excel in the topic of determinants. The step-by-step NCERT Mathematics solutions for exercises such as Exercise 4.1, Exercise 4.2 and NCERT Book Exercise 4.3 simplify complex mathematical operations, like evaluating determinants and finding minors and co-factors. NCERT Textbook Math solutions for Class 12 Determinants Miscellaneous Exercise ensure students get ample practice for advanced problems.
Class 12 Mathematics Book solutions are well-structured to align with board exam requirements and help students understand the application of determinants in solving real-world problems, such as system equations. NCERT Solutions for Class 12 Maths Chapter 4 PDF downloads provide easy access to study materials anywhere. By distributing their study time across all exercises, including Exercise 4.6, students can thoroughly cover the topic. These solutions make learning determinants simple and effective, boosting confidence for exams.
| Class: 12 | Mathematics |
| Chapter 4: | Determinants |
| Content: | NCERT Exercises Solution |
| Content Type: | Text, Videos and PDF Format |
| Session: | CBSE 2025-26 |
| Medium: | English and Hindi Medium |
Class XII Maths Chapter 4 solutions is given here. UP board solutions for class 12 Maths Chapter 4 are same as the NCERT Sols for 12th Maths Chapter 4. UP Board intermediate students are also using following NCERT Textbooks for new session, so they also can use these solutions for their help in problem solving. Other boards students like MP Board, Uttarakhand, and Gujrat Board can use these textbook solutions to prepare their exams. The solutions of questions are helpful for all the students who are using 12th NCERT Books. To understand the 12th Maths Chapter 4 properly, we must know everything about matrices. So, first learn the concepts of the chapter 3 Matrices to do Chapter 4 Determinants.
12th Maths Chapter 4 Solutions
In 12th Mathematics chapter 4 we shall study determinants up to order three only with real entries. The history about determinant is given below to know more about this fact. Download NCERT solutions for class 12 Maths chapter 4 determinants all six exercise with miscellaneous in PDF format. UP Board Solutions for Class 12 Maths Chapter 4 is same as NCERT Sols for 12th Maths Chapter 4 Determinants. So, UP Board students can also take the benefits of these solutions.

Class 12 Maths Chapter 4 Study Material
- Download Class 12 Maths NCERT Chapter 4
- Class 12 Maths Revision Book Chapter 4
- Class 12 Maths Revision Book Answers
- Class 12 Maths Download Assignment 1
- Class 12 Maths Download Assignment 2
- Class 12 Maths Download Assignment 2 Answers
- Class 12 Maths Download Assignment 3
- Class 12 Maths Download Assignment 4
- Class 12 Maths NCERT Solutions
- Class 12 all Subjects NCERT Solutions
Properties of Determinants
If all the rows of a determinant are converted into the corresponding columns, the value of the determinant remains same.
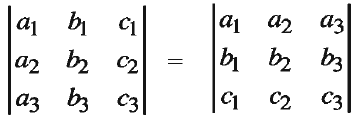
If two rows (columns) of a determinant are interchanged, the value of the new determinant is the additive inverse of the value of the given determinant.
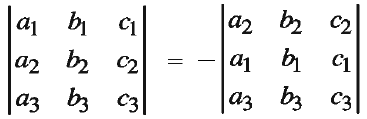
The value of a determinant gets multiplied by k, if every entry in any of its row (column) is multiplied by k.
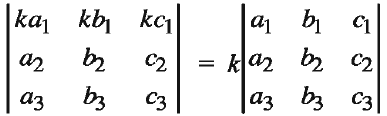
If some or all elements of a row or column of a determinant are expressed as sum of two (or more) terms, then the determinant can be express as sum of two (or more) determinants.
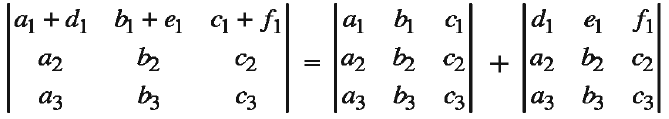
If the corresponding entries in any two rows ( or columns) are identical, the value of the determinant is zero.
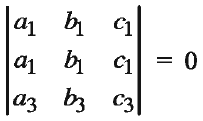
The value of a determinant does not changes if any of its rows (columns) is multiplied by non-zero real number k and added to another row (column).
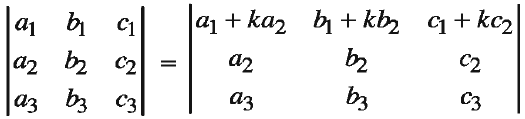
MINORS AND COFACTORS
Minor – Removing entries of the column and the row containing a given element of a determinant and keeping the surviving entries as they are, yields a determinant called the minor of the given element.
Cofactor – If we multiply the minor of an element by (-1)^(i+j), where i is the number of the row and j is the number of the column containing the element, then we get the cofactor of that element.
Historical Facts
- The Chinese early developed the idea of subtracting columns and rows as in simplification of a determinant using rods. Seki Kowa, the greatest of the Japanese Mathematicians of seventeenth century in his work ‘Kai Fukudai no Ho’ in 1683 showed that he had the idea of determinants as well as their expansion.
- T. Hayashi, “The Fakudoi and Determinants in Japanese Mathematics,” in the proc. of the Tokyo Math. Soc., V. Vendermonde was the first to recognise determinants as independent functions. He may be called the formal founder.
- Laplace (1772), gave general method of expanding a determinant in terms of its complementary minors.
- Lagrange, in 1773, treated determinants of the second and third orders and used them for purpose other than the solution of equations.
- Gauss, in 1801, used determinants in his theory of numbers.
- Jacques – Philippe – Marie Binet, in 1812, stated the theorem relating to the product of two matrices of m-columns and n-rows, which for the special case of m = n reduces to the multiplication theorem.
- Cauchy, in 1812, presented one on the same subject. He used the word ‘determinant’ in its present sense. He gave the proof of multiplication theorem more satisfactory than Binet’s.
- The greatest contributor to the theory was Carl Gustav Jacob Jacobi, after this the word determinant received its final acceptance.
Why are NCERT Solutions for Class 12 Maths Chapter 4 Determinants important for board exams?
NCERT Textbook Solutions for Class 12 Maths Chapter 4, Determinants, are essential for board exams because they provide a clear understanding of the topic and help students solve determinant-based problems efficiently. The solutions cover all exercises, including Exercise 4.1 and Exercise 4.3, explaining concepts like minors, co-factors and properties of determinants step-by-step. Miscellaneous Exercise Chapter 4 offers advanced practice for solving complex problems. With downloadable PDFs, students can easily revise solutions before exams. By practicing these solutions regularly, students can develop problem-solving skills and apply determinants to real-world problems like solving linear equations and verifying collinearity, ensuring better exam preparation.
In which practical fields can students use determinants chapter 4 of 12th Maths?
Determinants have wide applications in Engineering, Science, Economics, Social Science, etc. Determinants have wonderful algebraic properties and occupied their proud place in linear algebra because of their role in higher-level algebraic thinking.
How can NCERT Solutions for Class 12 Maths Chapter 4 PDF help students study effectively?
NCERT Verified Solutions for Class 12 Mathematics Chapter 4 PDF provides students with a convenient way to study and revise determinants. These PDF solutions cover all exercises, including Exercise 4.2, NCERT Exercise 4.4 and Exercise 4.6, offering detailed explanations for each question. The solutions simplify complex topics like calculating determinants of matrices, finding the inverse of a matrix and solving system equations. With offline access, students can study at their own pace and focus on specific problem areas. Practicing Class 12 Mathematics Determinants Miscellaneous Exercise questions from the PDF ensures students are well-prepared for both board exams and competitive exams, making the solutions a valuable resource.
Which main topics will students study in chapter 4 of class 12th Maths?
In chapter 4 of class 12th Maths, students will study determinants up to order three only with real entries. Also, students will study various properties of determinants, minors, cofactors and applications of determinants in finding the area of a triangle, adjoint and inverse of a square matrix, consistency and inconsistency of the system of linear equations and solution of linear equations in two or three variables using the inverse of a matrix.
What topics are covered in Class 12 Maths Chapter 4 Determinants NCERT Solutions?
Class 12 Maths Chapter 4 Determinants NCERT Textbook Solutions cover a variety of topics essential for mastering the subject. The exercises, such as Exercise 4.5 and NCERT Exercise 4.6, focus on calculating determinants, using their properties and applying them to find minors, cofactors and the adjoint of matrices. The solutions also include the application of determinants in solving linear equations, calculating the area of triangles and verifying collinearity. The Miscellaneous Exercise Chapter 4 offers advanced-level problems, enhancing problem-solving skills. By practicing these solutions, available in PDF format, students can strengthen their understanding and prepare thoroughly for exams.
Can students do chapter 4 Determinants of 12th Maths without going through chapter 3?
Students can’t do chapter 4 of class 12th Maths without doing chapter 3 of class 12th Maths. Before starting chapter 4, Determinants of class 12th Maths, students should first do chapter 3 Matrices of grade 12th Maths. Chapter 3 Matrices of class 12th Maths works as a base for chapter 4 Determinants of grade 12th Maths.
Does chapter 4 of grade 12th Maths has any miscellaneous exercise?
Chapter 4 of grade 12th Maths has a miscellaneous exercise. There are six exercises in chapter 4 of class 12th Maths, and the last exercise is the miscellaneous exercise of chapter 4 of grade 12th Maths. In the first exercise, there are eight questions. The second exercise has 16 questions. The third exercise contains five questions. There are five questions in the fourth exercise. In the fifth exercise, there are 18 questions. There are 19 questions in the last (Miscellaneous) exercise.


