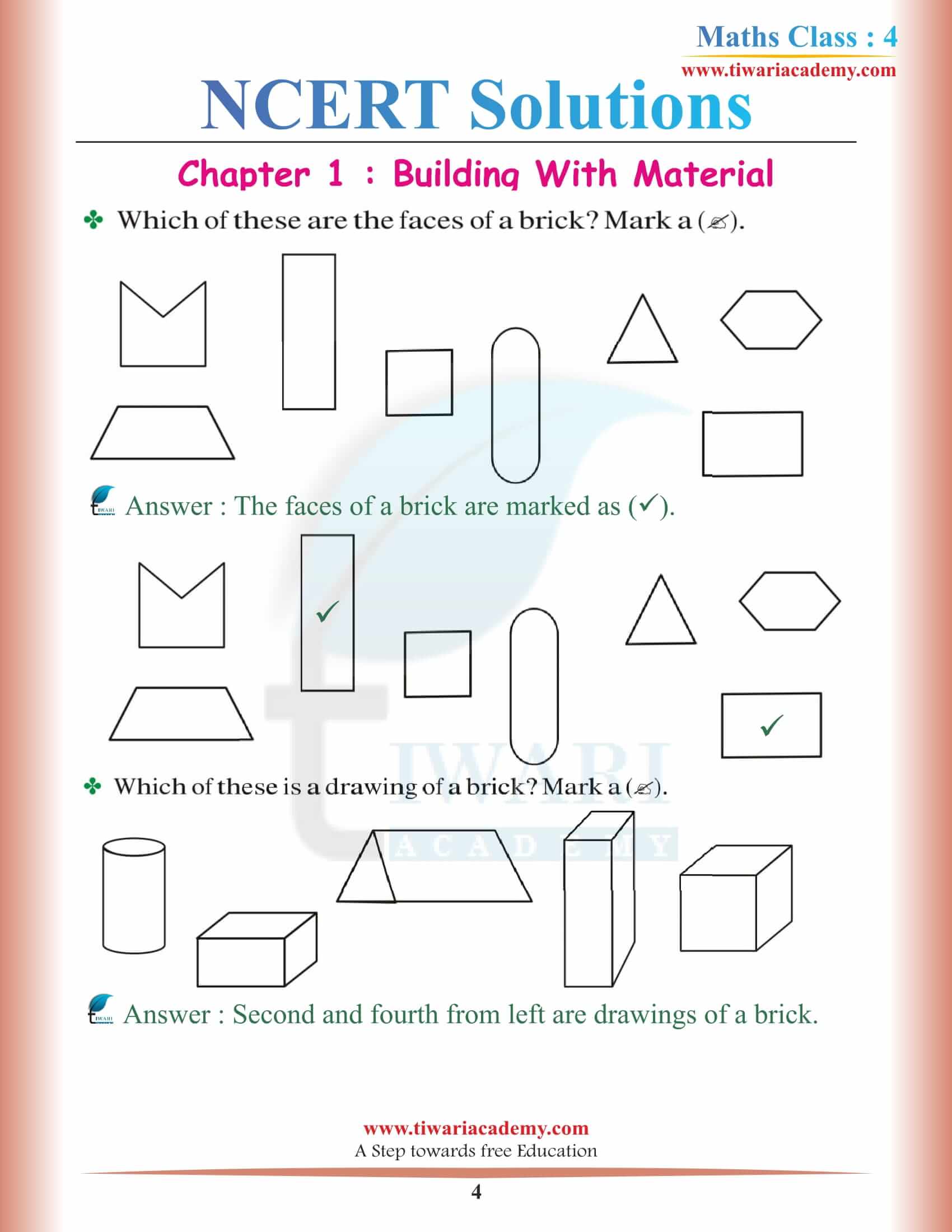
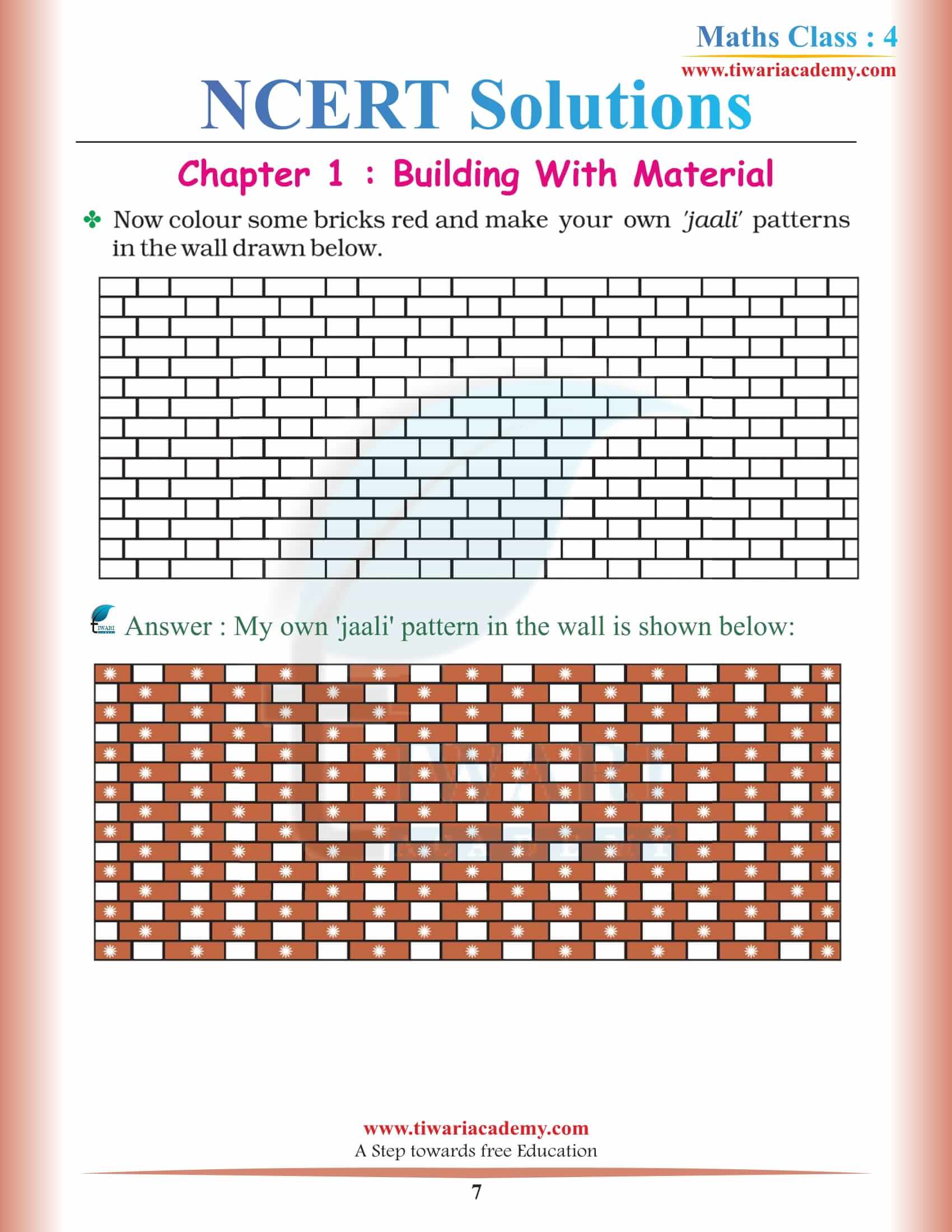
NCERT Solutions for Class 4 Maths Mela Chapter 1 Shapes Around Us

Page 1

Try to make a model of the buildings shown here using blocks.

1. What parts of the building have you shown in your model (for example, roof, pillars, base, etc.)?
See AnswerThe model of India Gate include parts like base, pillars, arches and the top structure.

2. Why did you select these parts?
See AnswerThese parts were selected because they represent the main structural elements of India Gate that make it recognizable.

3. What shapes will model these parts well?
See AnswerRectangular blocks for the base, cylindrical shapes for pillars, arch-shaped blocks for the archway and cuboid blocks for the top structure.

4. How is your model similar to the picture of the real building?
See AnswerThe model is almost similar in its overall structure, proportions and arrangement of key elements like the arches and pillars.

5. How is it different from the real building?
See AnswerThe model is different in scale, lacks detailed carvings and inscriptions. It is made of simple geometric shapes rather than stone.

Discussion:

1. What would happen if you removed one piece of your model? Would the model still look like the original building?
See AnswerIf a key piece like an arch or pillar was removed, the model would no longer resemble India Gate properly.
2. In what ways could you make the model even better?
See AnswerThe model could be improved by adding more details, using better proportions, adding color or creating inscriptions with paper.

Page 2

Project Work

Encourage learners to observe a street carefully and make a modal showing the main buildings on the street. 
See AnswerMaterials You Can Use:
1. Empty matchboxes or cardboard
2. Chart paper
3. Glue and scissors
4. Sketch pens or crayons
5. Straws (for lamp posts or poles)
6. Small boxes or bottle caps (for huts and tanks)
What to Include in the Model:
Here are some main buildings/structures you can make:
1. Houses (use small boxes or draw them on paper)
2. Shops (colorful and a bit bigger than houses)
3. School or Hospital (a taller box with a name label)
4. Streetlights (use straws)
5. Road (use black paper with white stripes)
6. Water tank or Dustbin (bottle caps or small containers)
7. Trees (green paper or draw them)

1. Do you think it looks like the Qutub Minar?
See AnswerYes, the model shown has a tall, tapering structure similar to Qutub Minar.

2. What shape would you use if you made a model of the Qutub Minar? Why?
See AnswerI would use cylindrical shapes stacked in decreasing sizes (from bottom to top) because Qutub Minar is a tapering tower with circular cross-sections at different levels.

3. How many such shapes will you use?
See AnswerFive cylindrical shapes, as the Qutub Minar has 5 storeys.

4. Earlier, people made buildings with clay bricks, stone blocks or wood. Today we also use concrete blocks, hollow blocks, etc.  What is common to all bricks (clay bricks, stone blocks, wood, concrete blocks, hollow blocks)?

See AnswerAll these bricks have a defined geometric shape, flat surfaces, straight edges and can be arranged in a pattern to create structures.

Page 3

Craft

1. Make a sphere-like shape with paper strips.
See AnswerThis is a craft activity where paper strips are interwoven in a crisscross pattern to create a sphere-like structure.
2.  Use the nets given at the end of the book to make the models shown (prisms and pyramids).

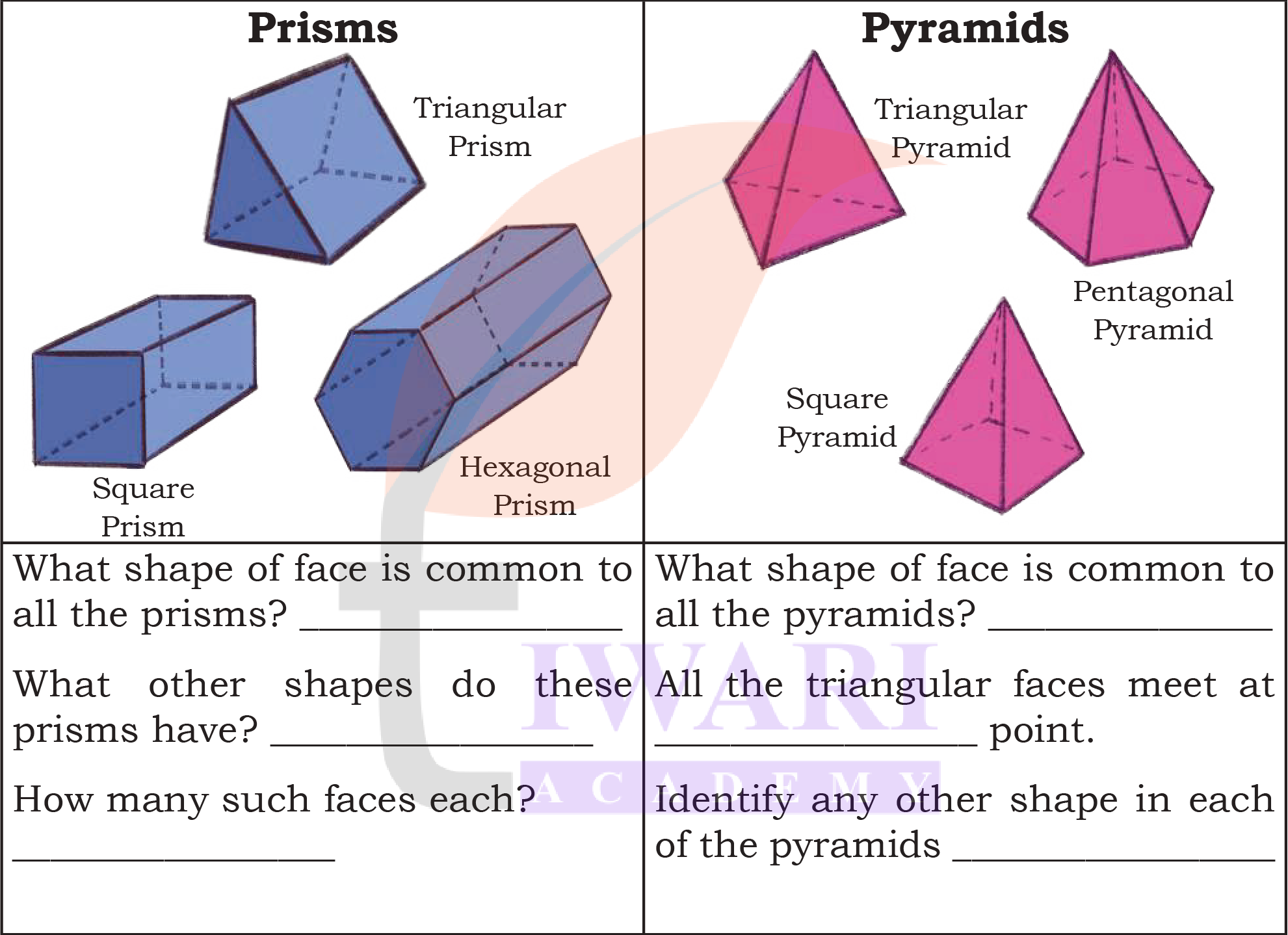
See AnswerFor Prisms:
(a) Rectangles (or squares) are common to all prisms.
(b) Triangles (in triangular prism), squares (in square prism), pentagons (in pentagonal prism) and hexagons (in hexagonal prism).
(c) 2 faces each (at the ends of the prism).
For Pyramids:
(a) Triangular faces are common to all pyramids.
(b) All triangular faces meet at one point (the apex or vertex).
(c) Triangular base (in triangular pyramid), square base (in square pyramid) and pentagonal base (in pentagonal pyramid).

Is a cube also a prism?
See AnswerYes, a cube is a special type of prism where all faces are squares. It’s specifically a square prism with equal length, width and height.

What is the difference between a prism and a pyramid?
See AnswerA prism has two identical polygon bases connected by rectangular faces, while a pyramid has one polygon base connected to a single vertex (apex) by triangular faces.

Page 4

3. Now try to make the above shape using straws and plasticine/ thread and fill in the table.

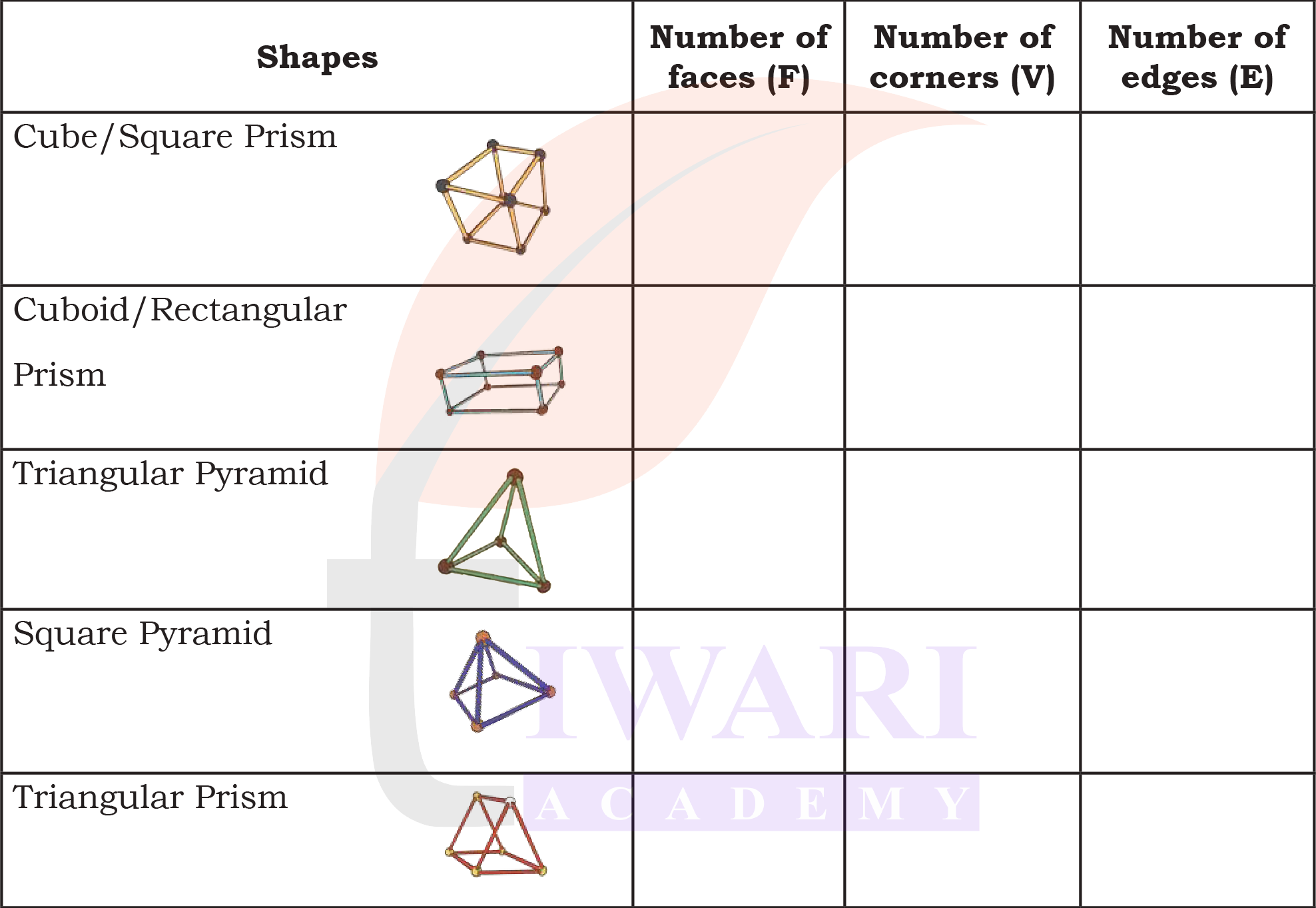
See AnswerShapes
(a) Cube/Square Prism
(b) Cuboid/Rectangular Prism
(c) Triangular Pyramid
(d) Square Pyramid
(e) Triangular Prism
Number of faces (F)
(a) 6
(b) 6
(c) 4
(d) 5
(e) 5
Number of corners (V)
(a) 8
(b) 8
(c) 8
(d) 5
(e) 6
Number of edges (E)
(a) 12
(b) 12
(c) 6
(d) 8
(e) 9

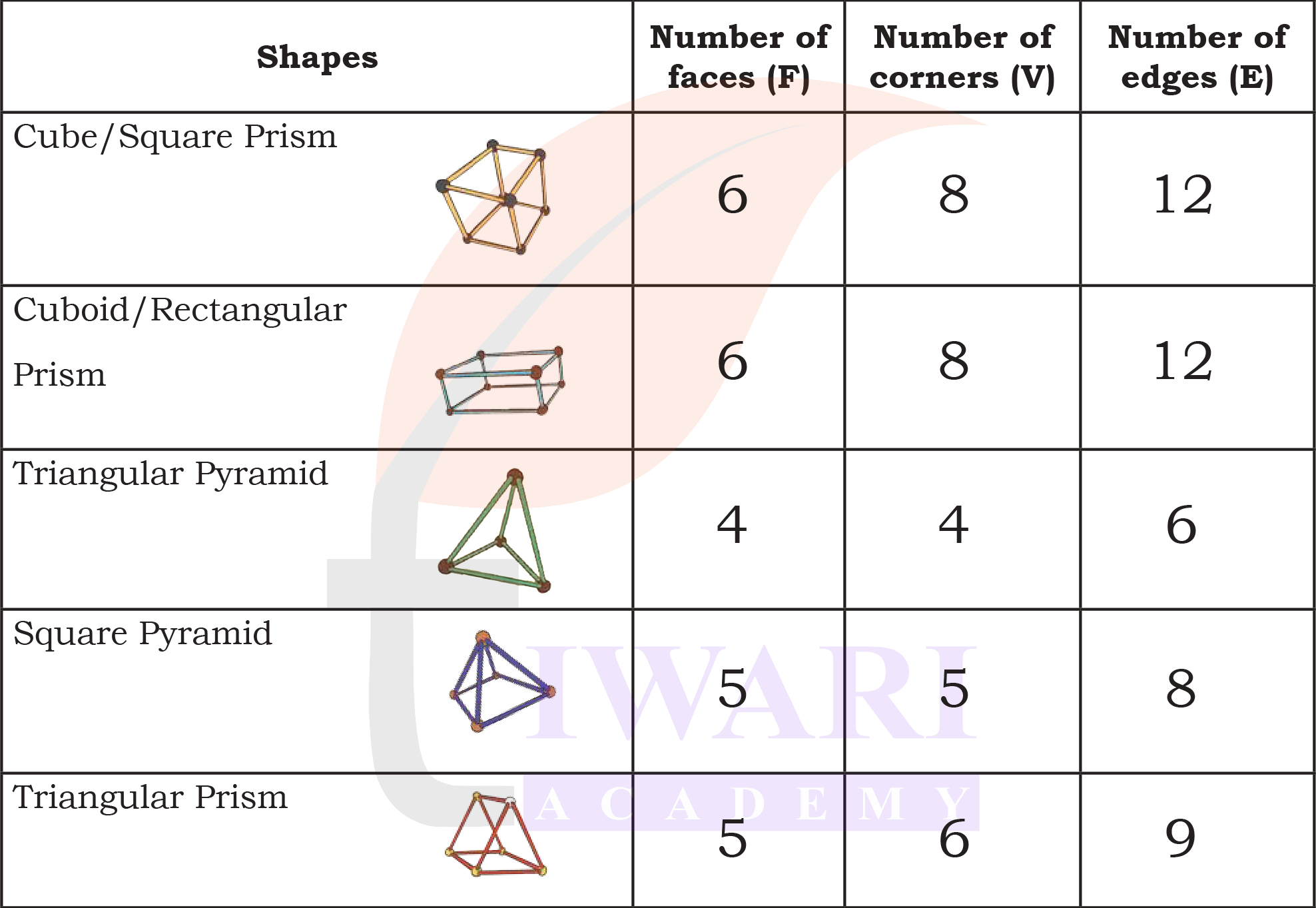
Identify any relationship that you may find between the number of faces (F), edges (E) and corners (V). Calculate F+V–E in each case. What do you notice?

See AnswerIn each case, F+V-E = 2. This is known as Euler’s formula for polyhedra.
Name of the shape
1 flat face: Cone
2 flat faces: Cylinder
4 flat faces: Triangular Pyramid
5 flat faces: Square Pyramid, Triangular Prism
6 flat faces: Cube, Cuboid
8 flat faces: Octahedron

Can you construct a 3D shape with 3 flat faces?

See AnswerYes, a tetrahedron (triangular pyramid) has 4 faces, but if one face is removed (making it open at the bottom), it would have 3 flat faces.
Name of the shape
6 straight edges: Triangular Pyramid
8 straight edges: Square Pyramid
9 straight edges: Triangular Prism
12 straight edges: Cube, Cuboid

Page 5

Let Us Observe

1. Take a die. Look at the face that has number 1. The face numbered 6 is opposite to the face numbered 1.
What is the face opposite to the
(a) face numbered 2?
See AnswerThe face opposite to 2 is 5.
b) What is the face opposite to the face numbered 3?
See AnswerThe face opposite to 3 is 4.
c) What is the face opposite to the face numbered 4?
See AnswerThe face opposite to 4 is 3.

2. a) Which faces have common edges with the face numbered 1?
See AnswerFaces numbered 2, 3, 4 and 5 have common edges with face 1.
b) Which face has no common edge with the face numbered 1?
See AnswerFace 6 has no common edge with face 1 (as it’s directly opposite).

3. Look at three different views of the same cube.

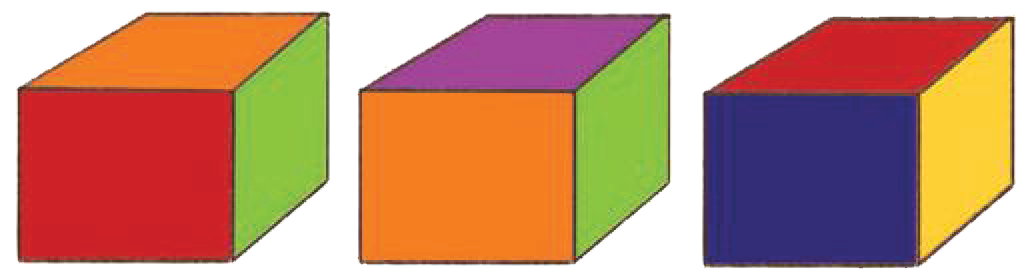
a) What colour is the face that is opposite to the red face?
See AnswerBlue is opposite to the red face.
b) What colour is the face that is opposite to the yellow face?
See AnswerGreen is opposite to the yellow face.

Page 6

Sorting 3D shapes

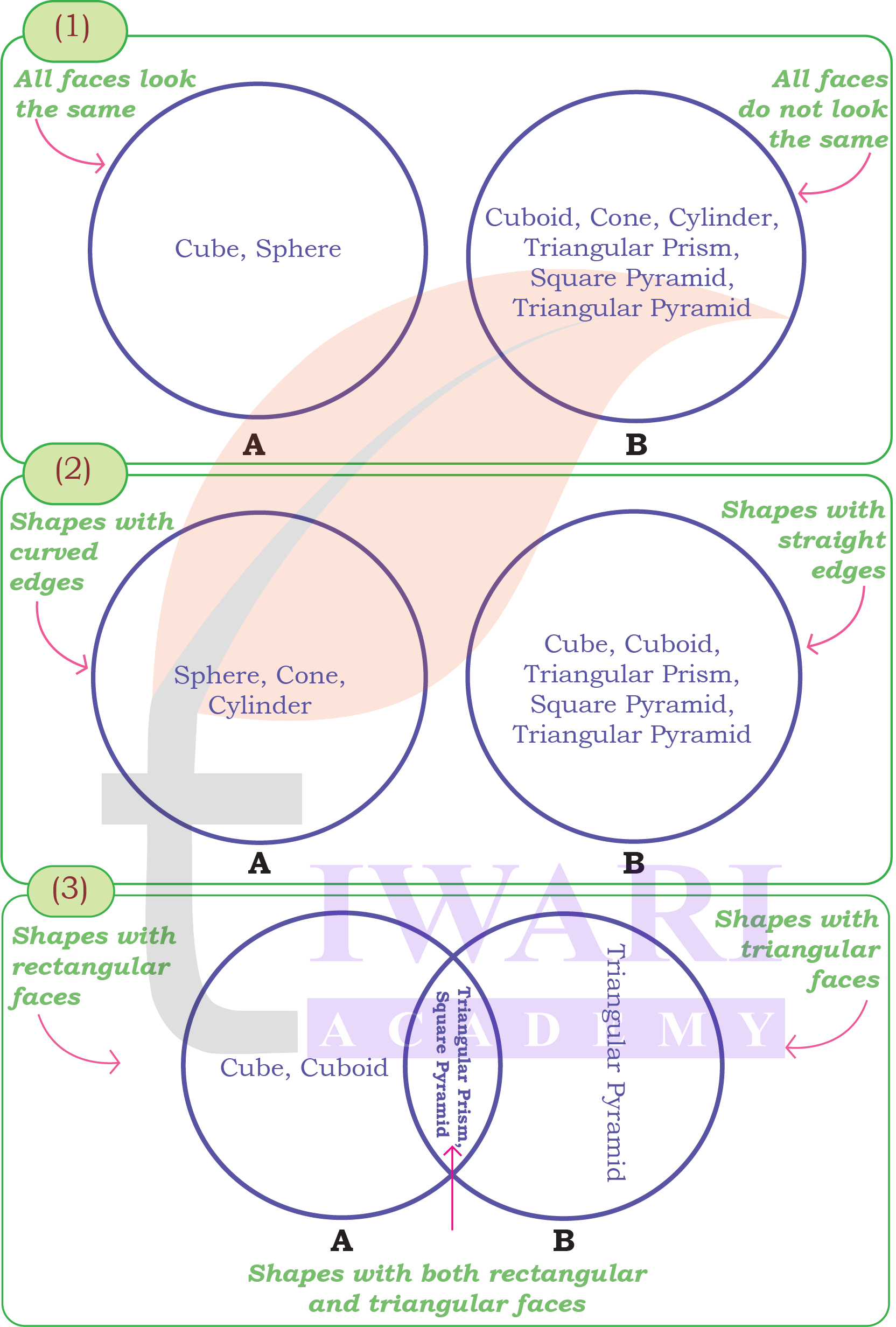
Write the names of 3D shapes in the correct places.

See AnswerFor Venn diagram (1):
Set A (All faces look the same): Cube, Sphere
Set B (All faces do not look the same): Cuboid, Cone, Cylinder, Triangular Prism, Square Pyramid, Triangular Pyramid
Intersection (shapes that fit both categories): None
For Venn diagram (2):
Set A (Shapes with curved edges): Sphere, Cone, Cylinder
Set B (Shapes with straight edges): Cube, Cuboid, Triangular Prism, Square Pyramid, Triangular Pyramid
Intersection (shapes that fit both categories): None
For Venn diagram (3):
Set A (Shapes with rectangular faces): Cube, Cuboid
Set B (Shapes with triangular faces): Triangular Pyramid
Intersection (shapes with both rectangular and triangular faces): Triangular Prism, Square Pyramid

Page 7

In which circle did you write triangular prism and rectangular pyramid?
See AnswerTriangular prism and rectangular (square) pyramid go in the intersection of Sets A and B in Venn diagram (3), as they have both rectangular and triangular faces.

Cube Towers

How many cubes are there in each of these cube towers?

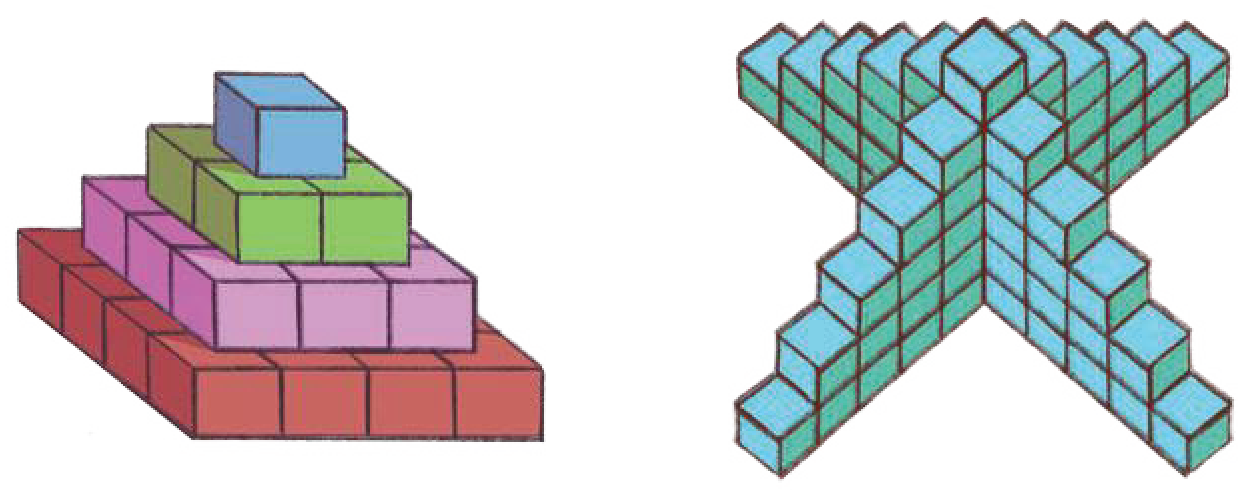
See AnswerIn first tower (rectangular tower) there are 30 cubes.
In Second tower, there are 66 cubes.

Page 8

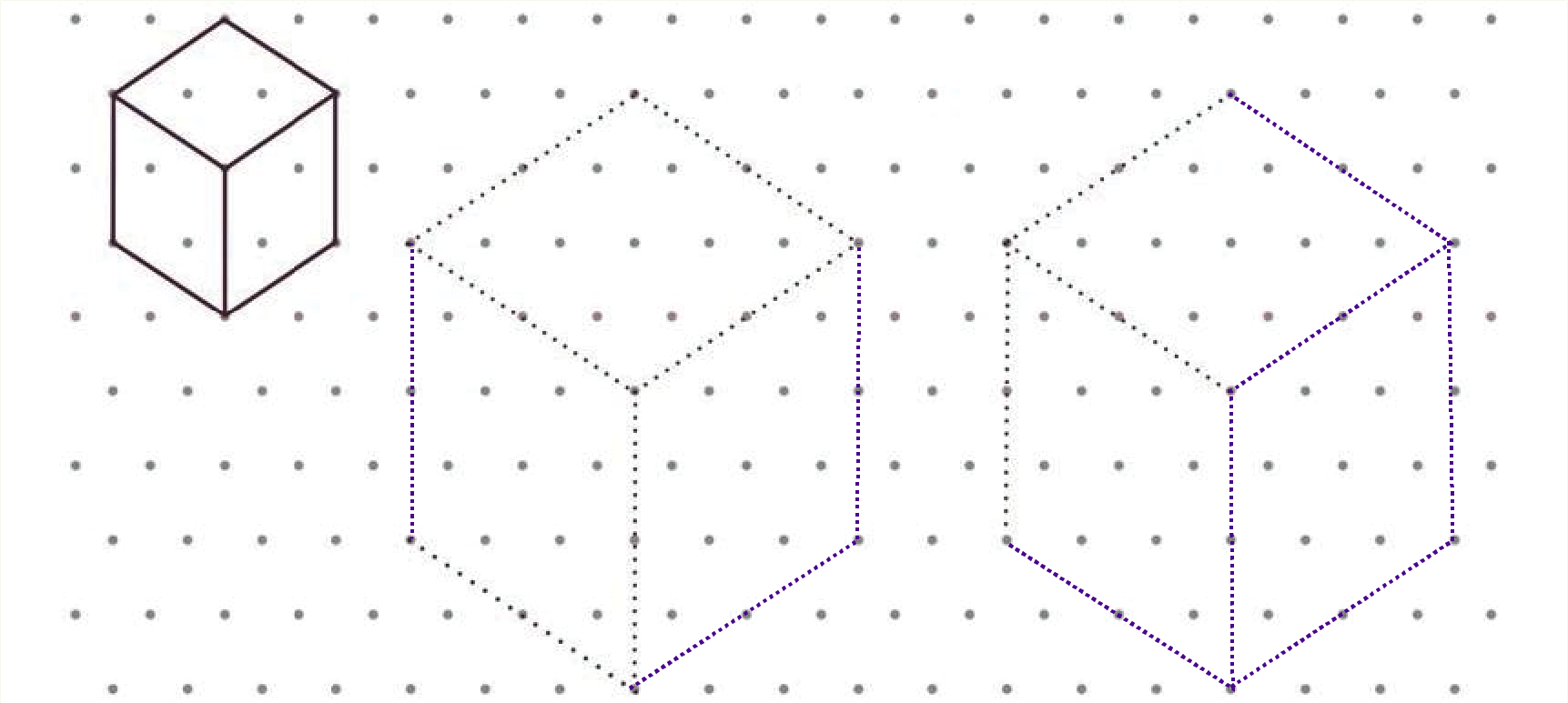
Drawing Cubes on a Triangular Dot Paper

Can you complete the following cubes?

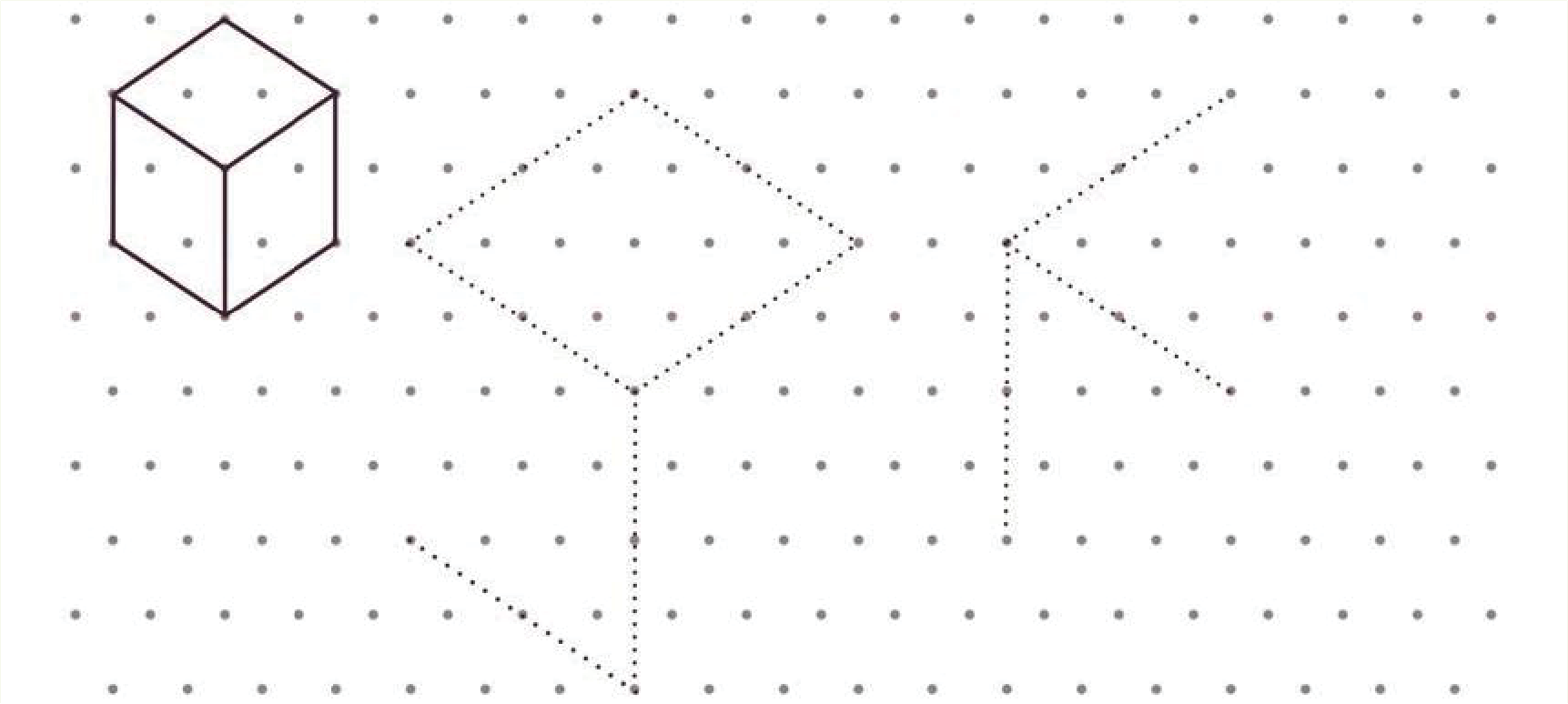
In the following way, we can complete the cubes:

1. Match the pictures to the descriptions and name the shapes.
a) I have 5 faces and 5 corners. I have 8 edges. 1 of my faces is a square and 4 of my faces are triangles.
AnswerSquare Pyramid
b) I have 1 flat face, 1 curved face, and 1 edge.
AnswerCone
c) I have 1 curved face. I have no edges or corners.
AnswerSphere
d) I have 2 flat faces, 1 curved face, and 2 edges. I have no corners.
AnswerCylinder
e) I have 5 faces, 6 corners, and 9 edges, and 2 of my faces are triangles.
AnswerTriangular Prism
f) I have 6 faces, 12 edges, and 8 corners.
AnswerCube or Cuboid

2. Each one is different. How? Discuss.

See Answer1. Red sphere: This is a perfectly round 3D shape with no edges or vertices. Every point on its surface is equidistant from its center.
2. Gold cone: This shape has a circular base that tapers to a single point (vertex) at the top. It has one curved surface and one flat circular surface.
3. Blue triangular pyramid (tetrahedron): This has four triangular faces, four vertices, and six edges. All faces are flat.
4. Green cube: This has six equal square faces, eight vertices and twelve edges. All faces are flat and meet at right angles.
5. Purple rectangular prism: Similar to the cube but with rectangular faces instead of squares. It has six rectangular faces, eight vertices and twelve edges.

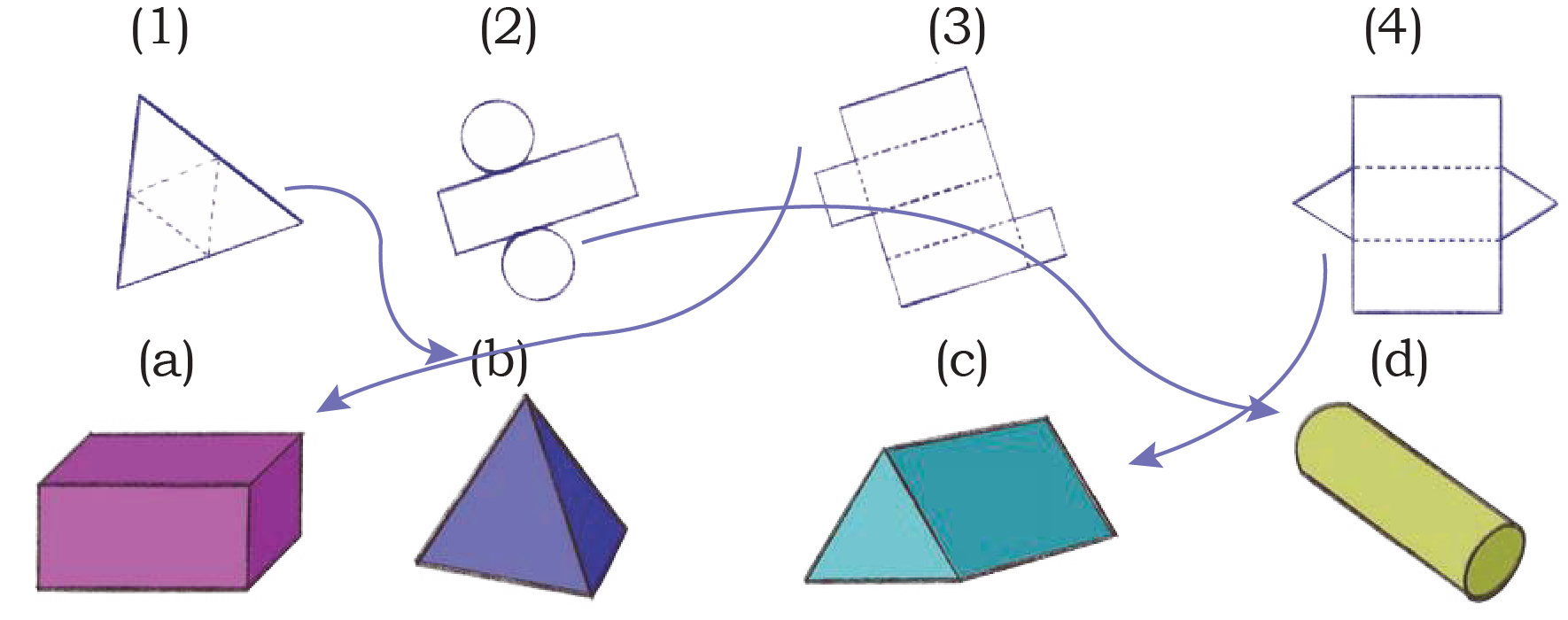
3. Match the following nets to the appropriate solids given below.

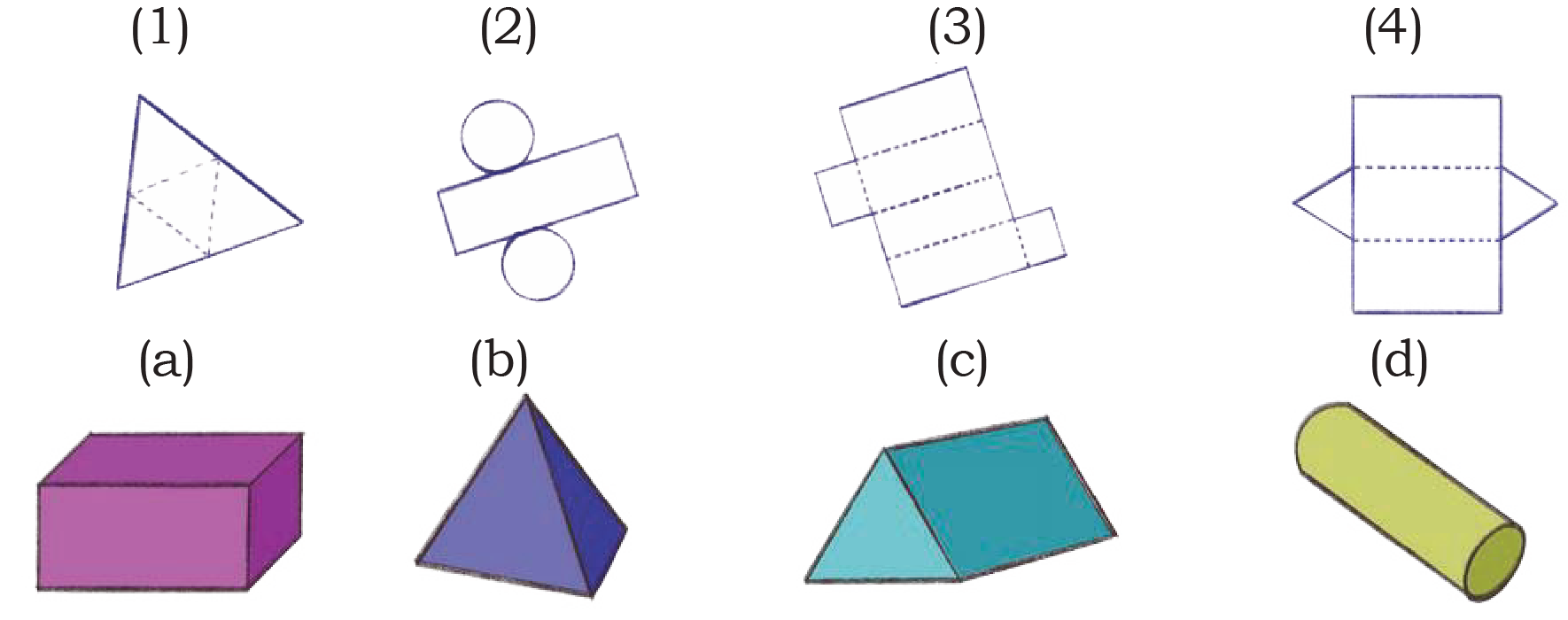
AnswerNet (a) matches with solid (3) – Triangular Prism
Net (b) matches with solid (4) – Cube
Net (c) matches with solid (1) – Triangular Pyramid
Net (d) matches with solid (2) – Square Pyramid

4. Which of these nets can be folded to make a solid of the kind given below?

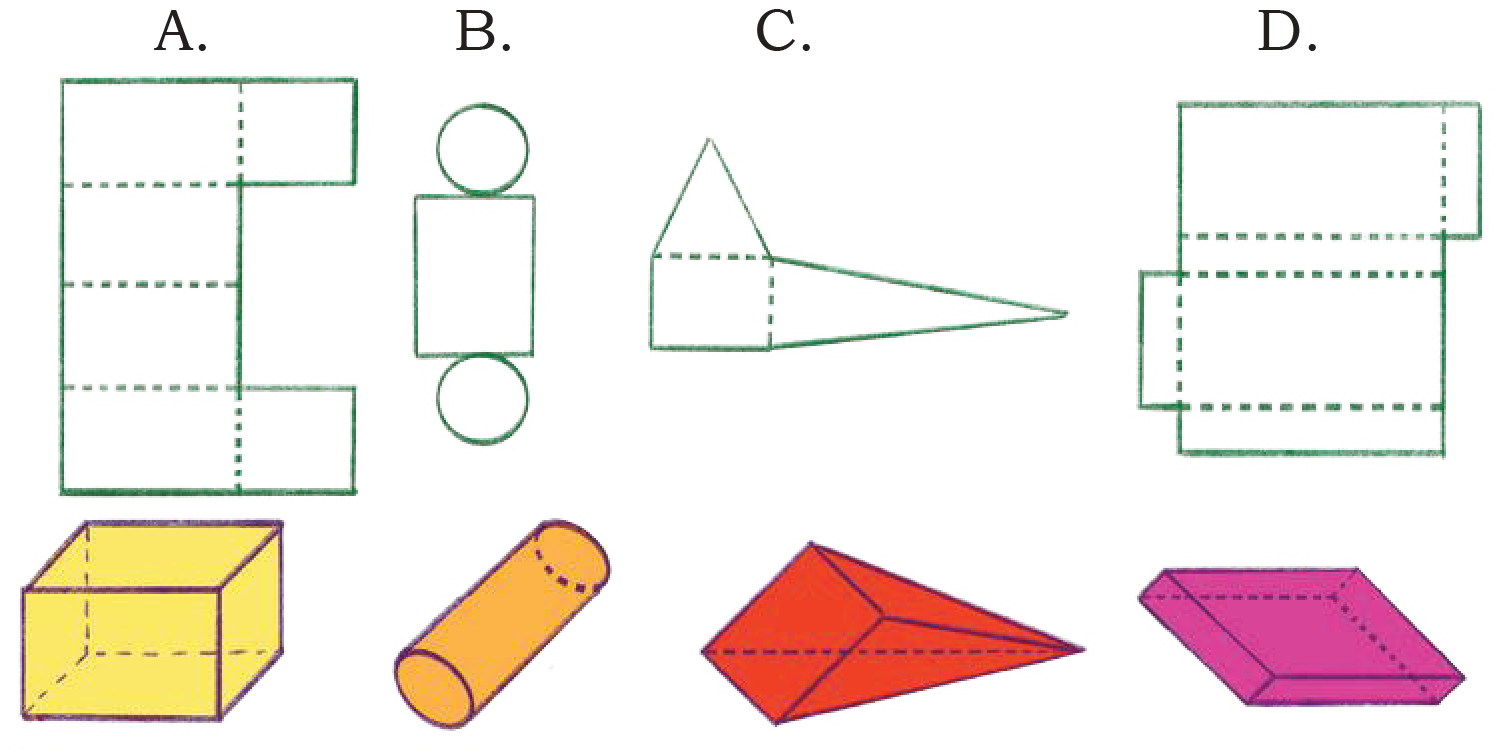
AnswerNets (a), (c) and (d) can be folded to make a cube.

5. Nitesh cuts up a net on the folds. Here are its pieces.

Which solid has the above pieces in its net?

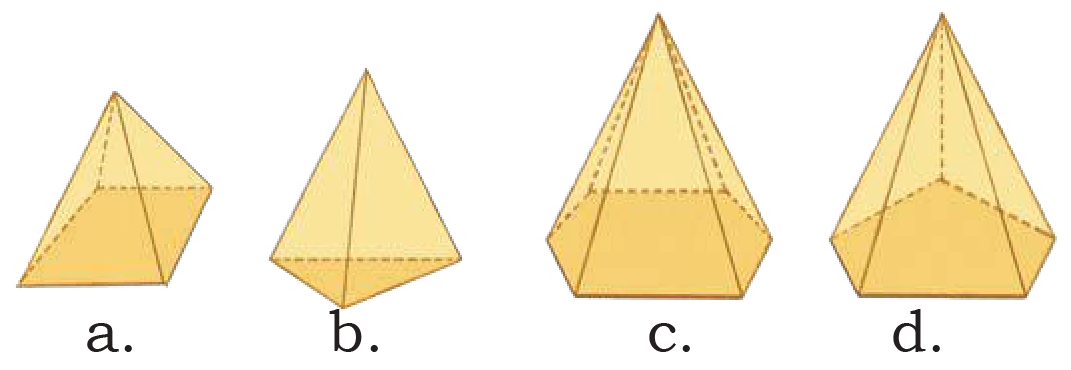
See AnswerThe pieces shown (a, b, c, d) form the net of a triangular prism.

Page 10

Let Us Do

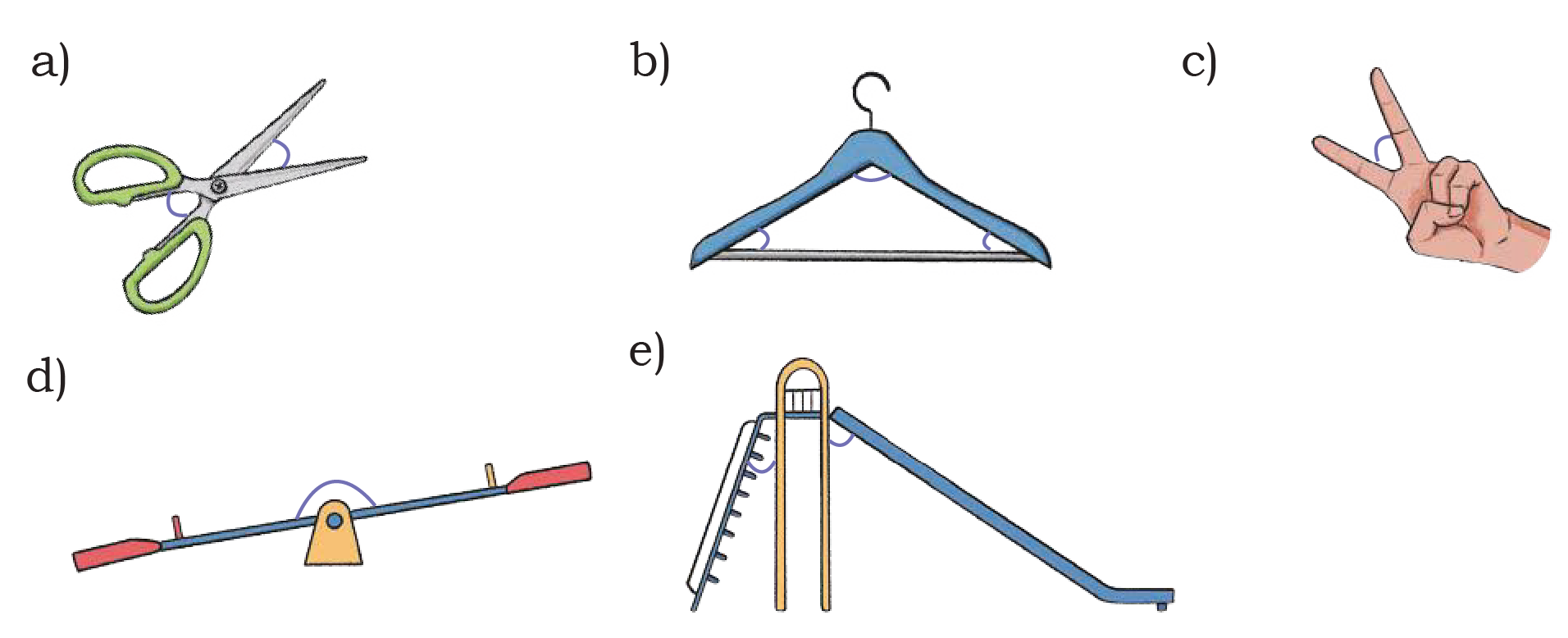
1. Mark the angles in the following pictures.

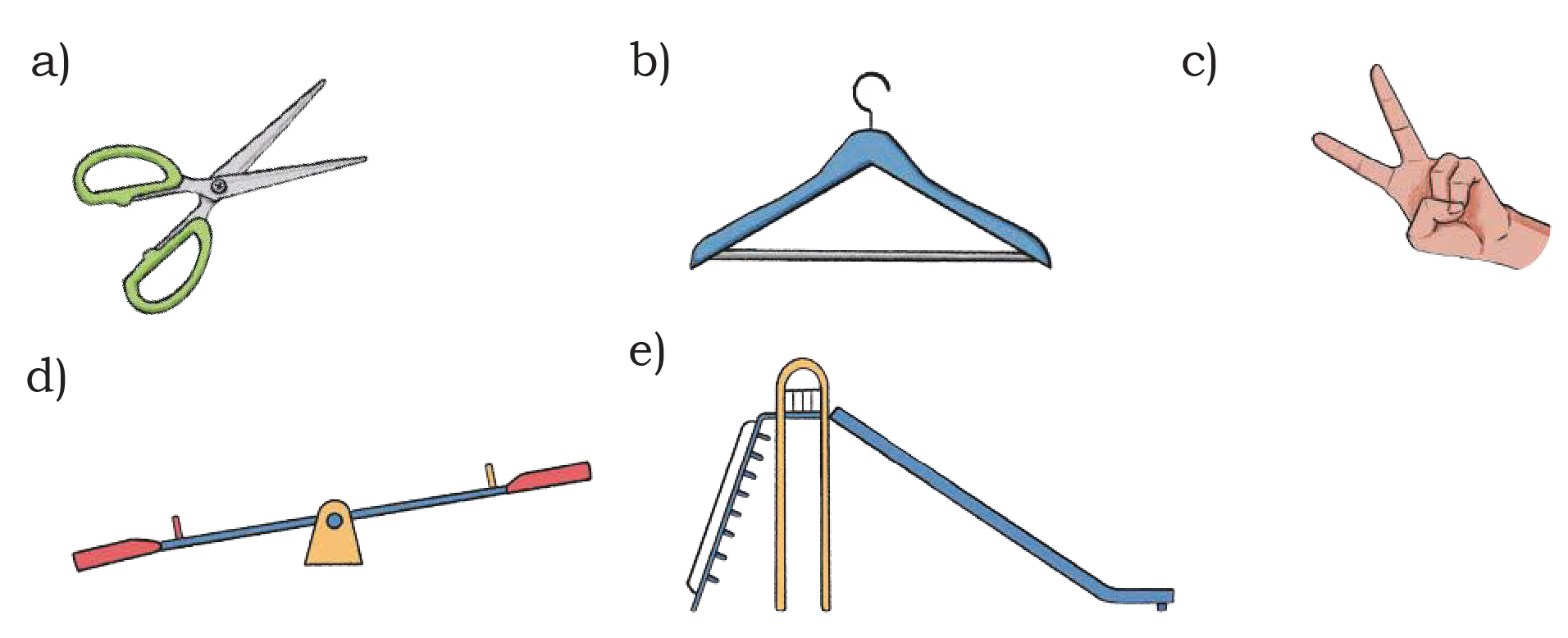
See Answera) Scissors: The angle is formed between the two blades of the scissors. When open, they form an acute angle (less than 90°).
b) Clothes hanger: The main angle is at the top/peak of the hanger where the two sides meet, forming an acute angle. There are also angles where the sides meet the bottom horizontal part.
c) Hand gesture: The fingers form an acute angle between them.
d) Seesaw: The angle changes depending on which side is up. When balanced, it would form a straight angle (180°) with the horizontal. When tilted, it forms obtuse and acute angles with the horizontal.
e) Playground slide: There are several angles here:
An acute angle between the slide and the ground
An acute angle between the ladder and the ground
Various angles where different components connect

2. Where do you see angles in the classroom? Give a few examples.
See AnswerAngles can be seen in corners of the room, edges of desks and tables, corners of books and notebooks, corners of blackboard/whiteboard, in scissor blades, in the hands of a clock, etc.

Page 11

Right Angles

(a) Let’s make a right angle with a piece of paper as shown.
See AnswerPerform this activity in your class.

(b) Identify the angles that you think are right angles and circle them in the dot grid below. Check using your angle checker.

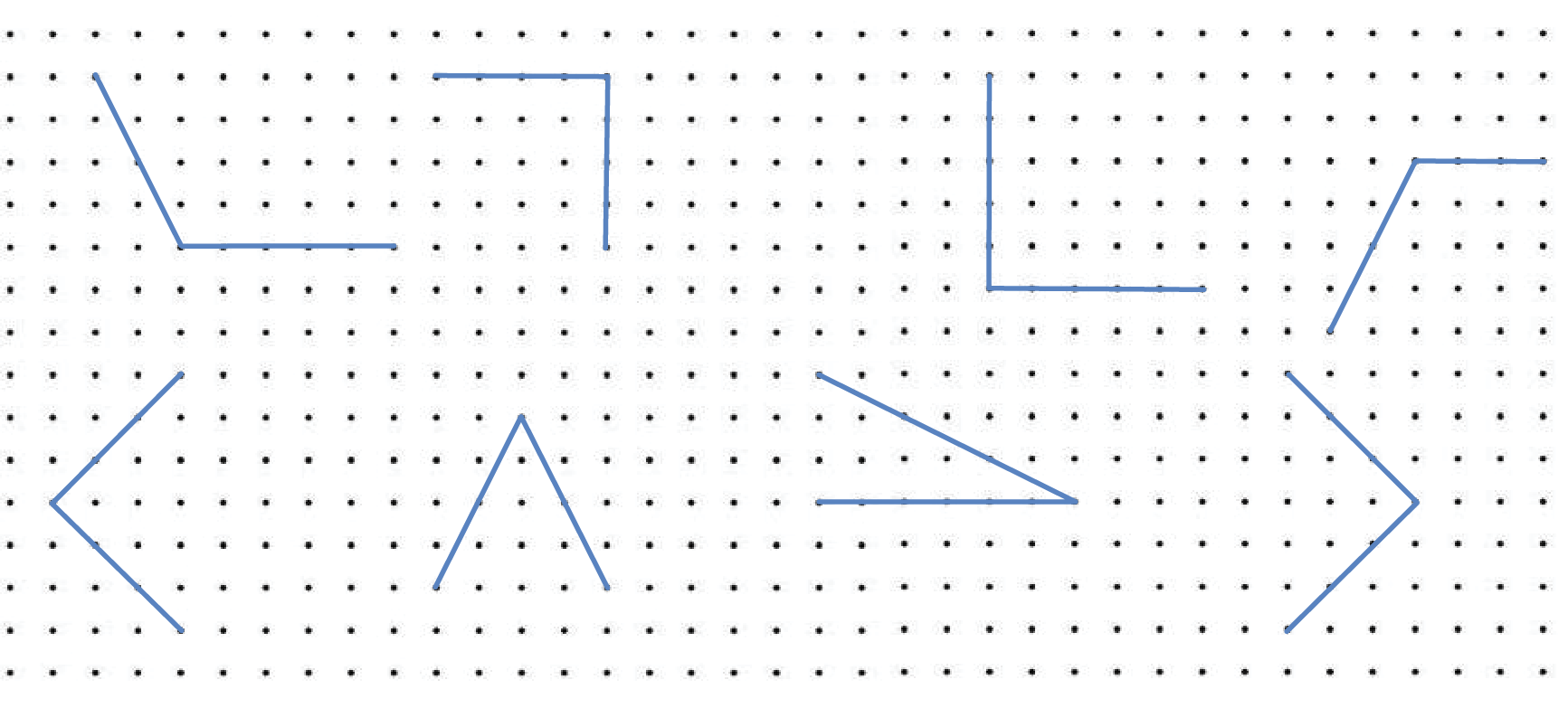
The following encircled are right angles:

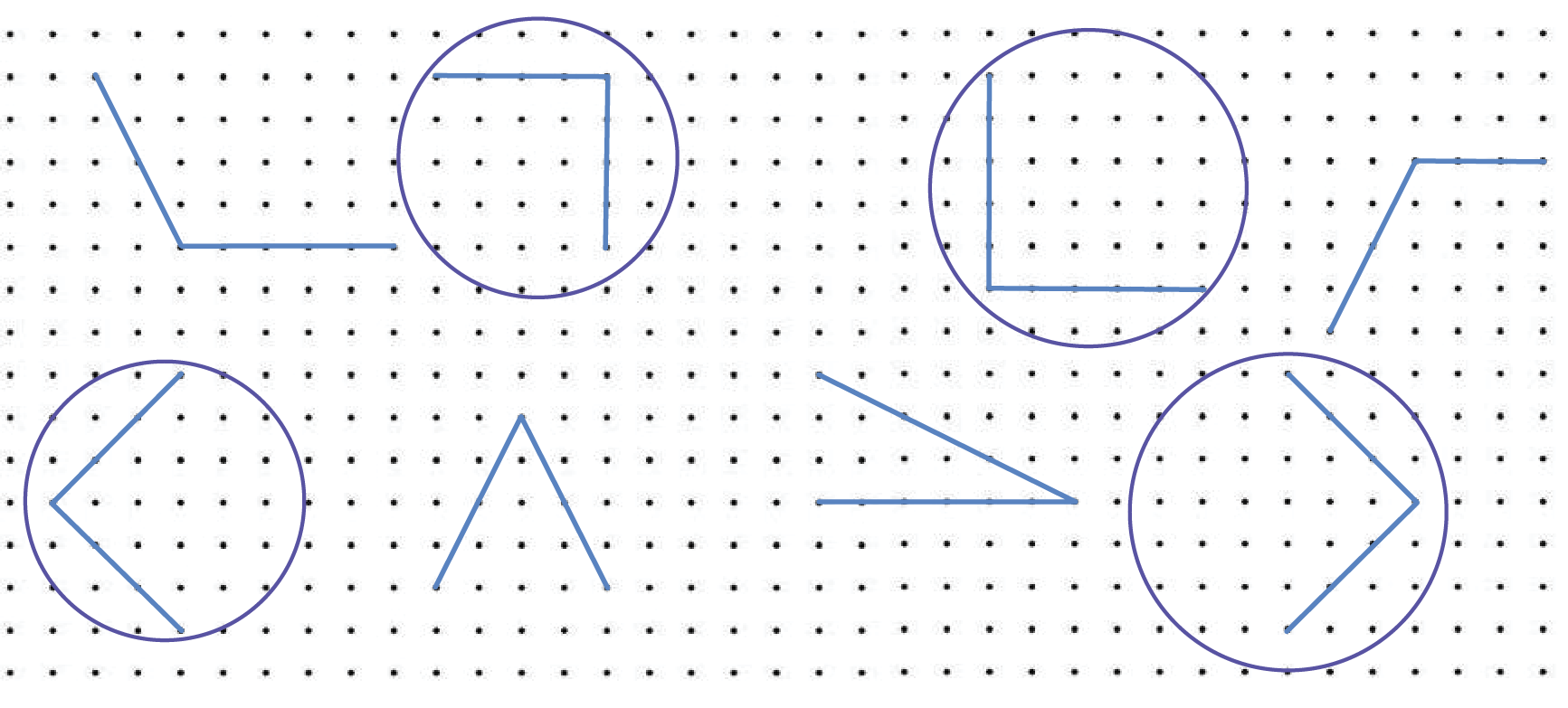
(c) Check for right angles in a book, window and any other object. Write the names of object where you find right angles.
See AnswerBook corners, window corners, door corners, table corners, blackboard corners, etc.

Page 12

Let Us Do

1. Draw some right angles on the dot grid.

The suggested answer is given below:

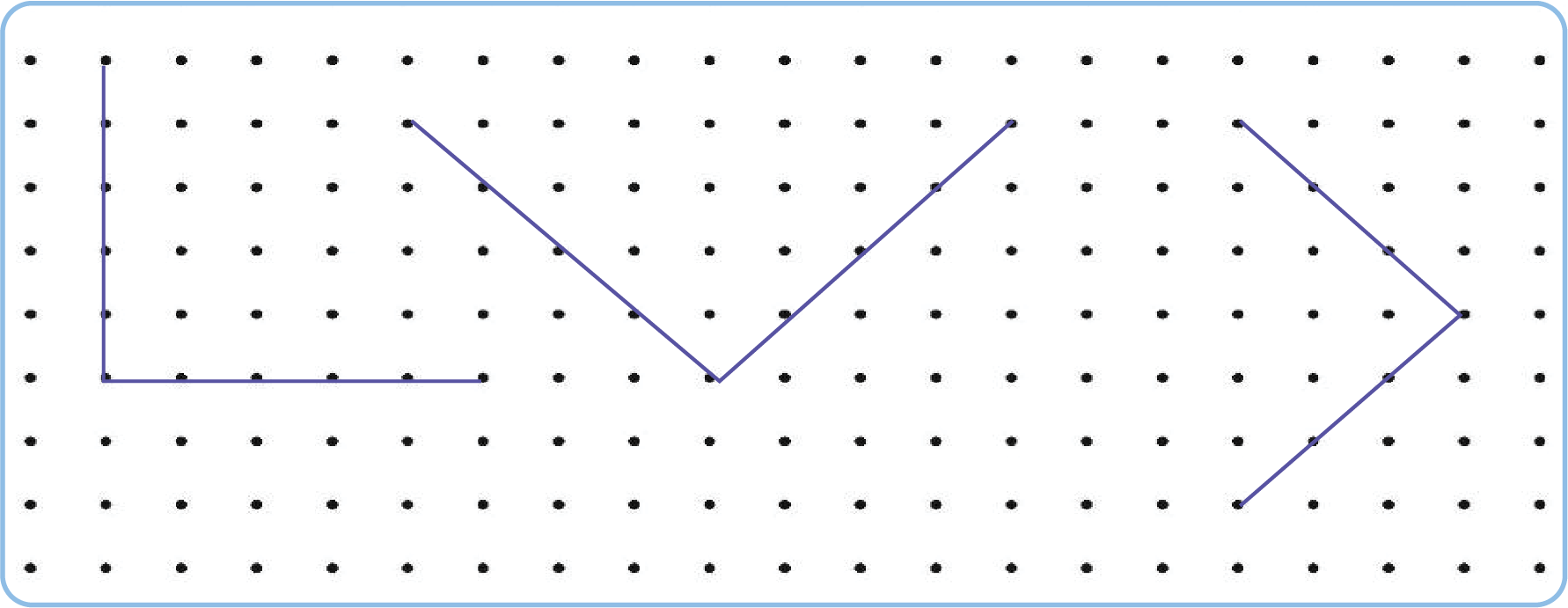
Name some objects from your classroom which have an acute angle.
See AnswerOpen scissors, clock hands at certain times (e.g., 11:30), slant of a pen stand, some chair designs.

Name some objects from your classroom which have an obtuse angle.
See AnswerOpen compass, certain roof designs, certain chair positions, partially open doors.

Identify all angles in the following letters.

See AnswerLetter V:
Contains 1 angle at the bottom point where the two lines meet (marked with a small curved line in the image)
Letter A:
Contains 2 angles: The top point where the two slanted lines meet
The interior angle where the horizontal crossbar meets the left slanted line (marked with a small curved line in the image)
Letter Z:
Contains 2 angles:
1. The upper right angle where the top horizontal line meets the diagonal line (marked with a small curved line in the image)
2. The lower left angle where the diagonal line meets the bottom horizontal line

Page 13

Let Us Do

1.

Answer:

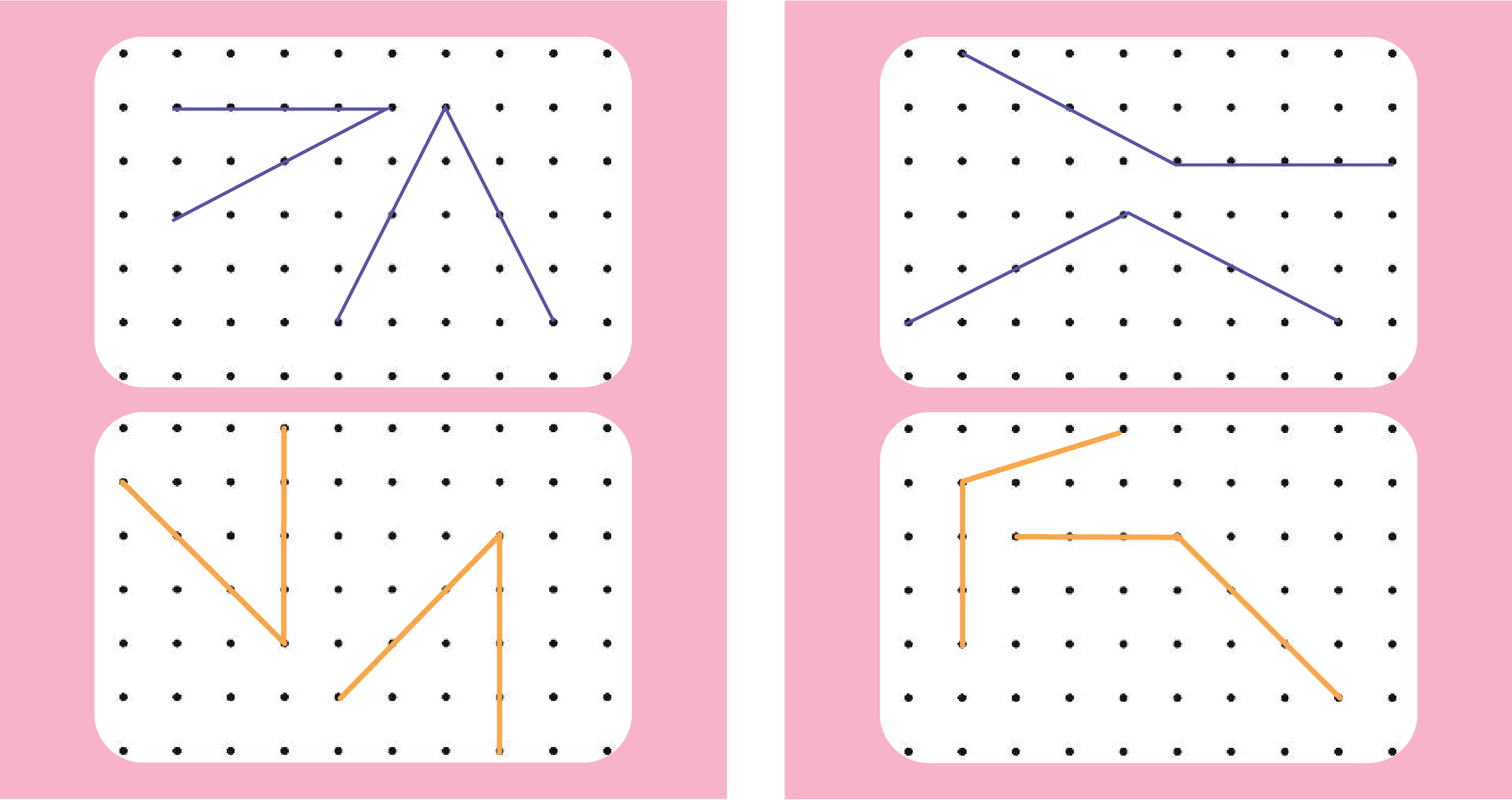
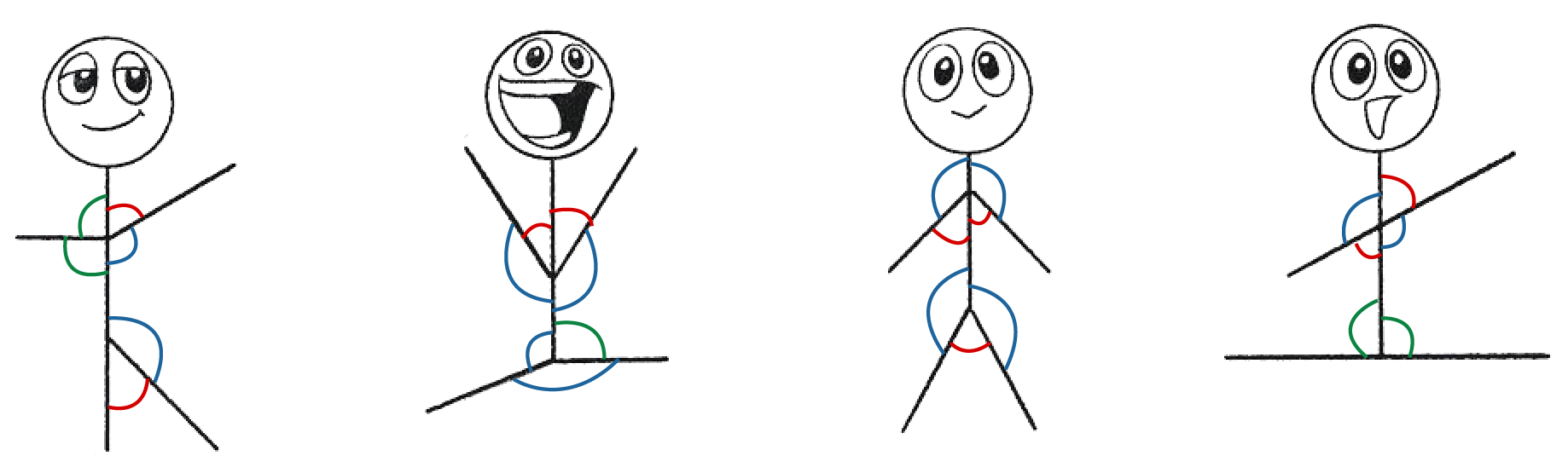
2. In the figures given below, mark the acute angles in red, right angles in green and obtuse angles in blue.

See AnswerFirst Figure (Leftmost):
Left Arm and Body: Forms a right angle (marked in green).
Right Arm and Body: Forms an acute angle (marked in red).
Right Leg and Body: Forms an obtuse angle (marked in blue).
Second Figure:
Both Arms: Form acute angles with the body (marked in red).
Right Leg and Body: Forms a right angle (marked in green).
Third Figure:
Both Arms and Legs: Appear to form acute angles (marked in red).
Fourth Figure (Rightmost):
Left Arm and Body: Forms an acute angle (marked in red).
Right Arm and Body: Forms a right angle (marked in green).

Page 14

Shapes with Straws

Make a triangle with straws of different sizes and clay/plasticine.
1. Does the shape of the triangle change if we gently push one of its sides?
See AnswerNo, triangles are rigid shapes.

2. What kinds of angles does a triangle have?
See AnswerA triangle can have acute, obtuse or right angles, depending on the specific triangle.

3. What kinds of angles do you see in the rectangle?
See AnswerFour right angles (90°).

4. Does the shape of the rectangle change if we gently push one of its sides?
See AnswerYes, it changes to a parallelogram.

5. What has happened to the angles of the new shape? Are they still right angles? What types of angles have been formed?
See AnswerThe angles are no longer right angles. Two acute angles and two obtuse angles have been formed.

6. Similarly, push one side of a square. Are they still right angles? What types of angles have been formed?
See AnswerNo longer right angles. Two acute angles and two obtuse angles have been formed.

7. How are the angles of triangles and rectangles similar or different?
See AnswerTriangles maintain their shape when pushed (rigid), while rectangles deform. A rectangle always has four right angles, while a triangle can have different types of angles.

Page 15

Use the dot grid given below to draw several three- angle and four-sided shapes. Circle the shapes that have one or more right angles.

See the figures encircled with one or more right angles:

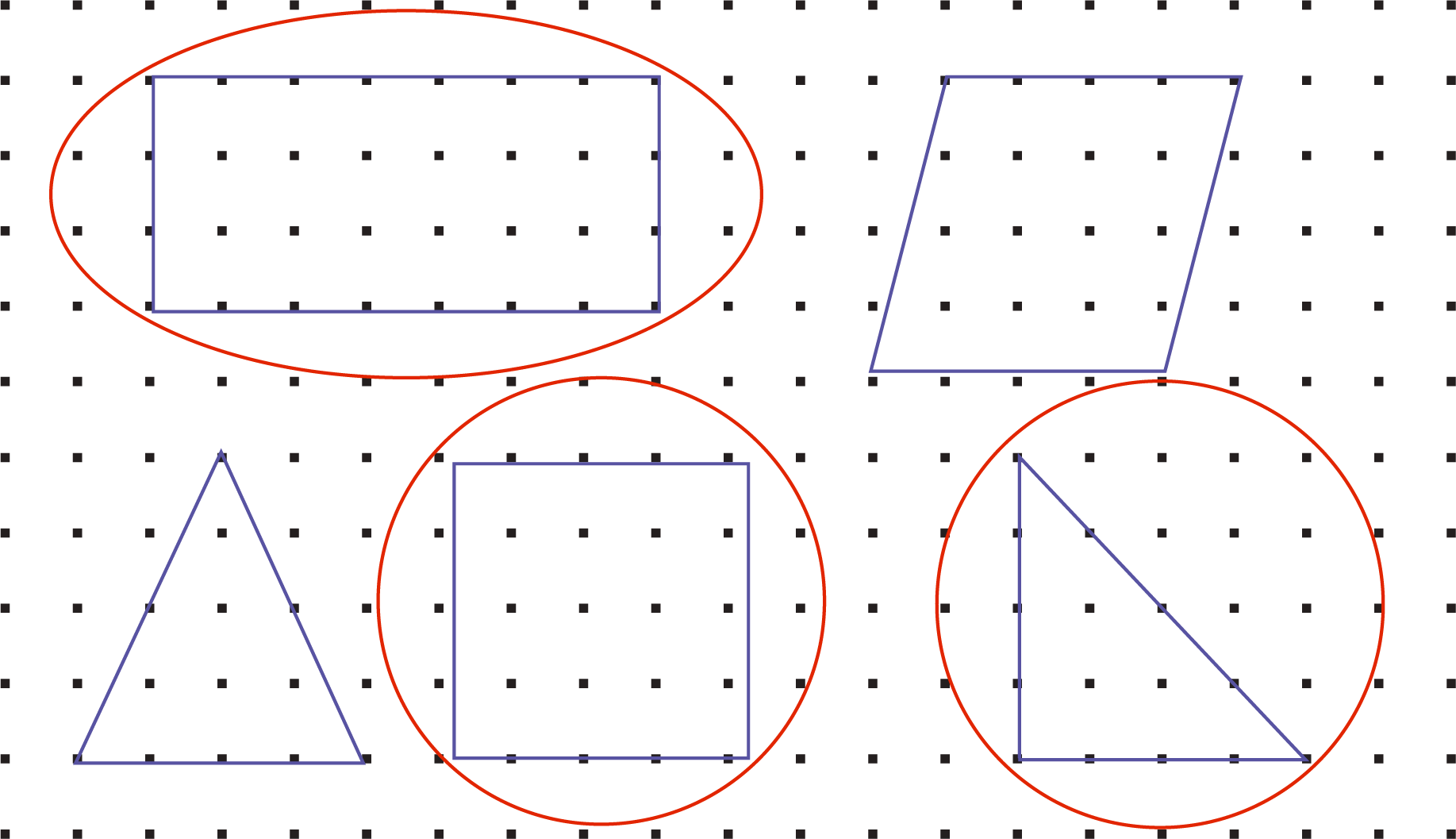
What shapes did you make? How many shapes have you made with:
a) 1 right angle
b) 2 right angles
c) 3 right angles
d) all right angles
See Answera) 1 Shape with 1 right angle
b) 0 Shape with 2 right angles
c) 0 Shape with 3 right angles
d) 2 Shapes with 4 right angles)

In what ways are rectangle and square different from these shapes?
See AnswerRectangles and squares have all right angles (4 right angles), while the other shapes have varying angles. Squares additionally have all sides equal.

Page 16

Try to make this 5-sided shape with all sides equal (Pentagon)
1. Are these right angles?
See AnswerNo, the angles in the pentagon are not right angles.
2. Does the shape of the pentagon change if we gently push one of its sides?
See AnswerYes, it changes shape.
3. How does this change the angles?
See AnswerSome angles become bigger (obtuse) and some become smaller (acute).

Can you make a circle using straws?
1. Look at the picture. The lengths of the straws in this picture are…
(Equal/Unequal)
See AnswerEqual
2. What will happen if we take straws of unequal lengths?
See AnswerThe circle will look uneven and will not be a perfect circle.

Page 17

Amazing Circles

1. The length of all the creases are _____.
See AnswerEqual
2. These creases are called diameters of the circle.
See AnswerYes, that’s correct.
3. Discuss where the centre is. Do you notice that all the diameters pass through the centre?
See AnswerThe center is where all diameters intersect. Yes, all diameters pass through the center.
4. Measure the length of the creases from the center to the border of the circle. This is called the radius of the circle.
See AnswerThe measurement would depend on the size of the circular paper used.
5. Discuss if there is any relationship between the radius and the diameter of a circle.
See AnswerThe diameter is twice the radius, or the radius is half the diameter.

Let Us Do

The length of the diameter is _____ (half/double) of the length of radius.
See AnswerDouble
Look at the carpet design. A beautiful circle, right?
Mark the centre, radius, and the diameter of the circular design with any colour of your choice.

See AnswerThis is a practical activity where students mark these elements on the given carpet design. For the help, a sample design is given below.

Page 19

Look at the wheels

All wheels look like……….
See AnswerCircles
Name the wheel with the:
1. Longest radius………. 
See AnswerB
2. Shortest radius………. 
See AnswerD
3. Longest diameter……….
See AnswerB
4. Shortest diameter……….
See AnswerD

Puzzling Shapes

1. Identify the hidden shapes and write their names.

See AnswerSquare, Rectangle, Triangle, Circle

2. Draw 2 lines to divide the triangle into 1 square and 2 triangle.

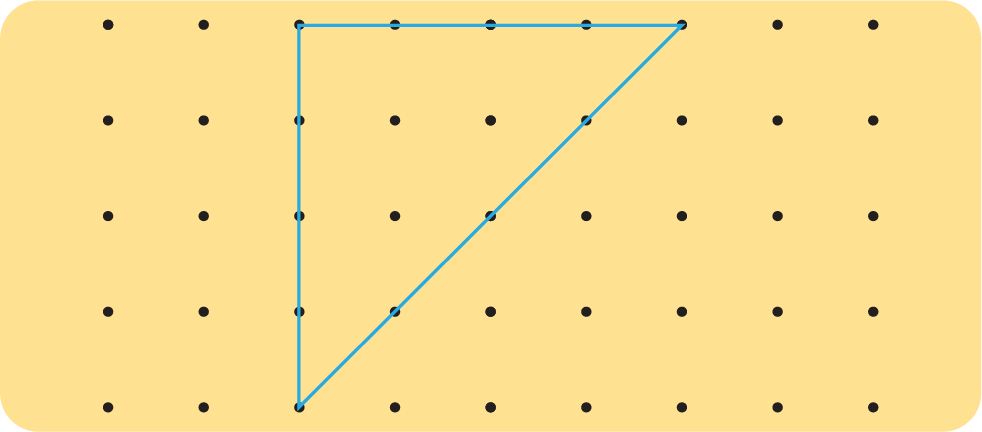
See AnswerYou can draw:
1 vertical line to make a square on the left
1 diagonal line from the top of the square to the bottom right corner of the triangle

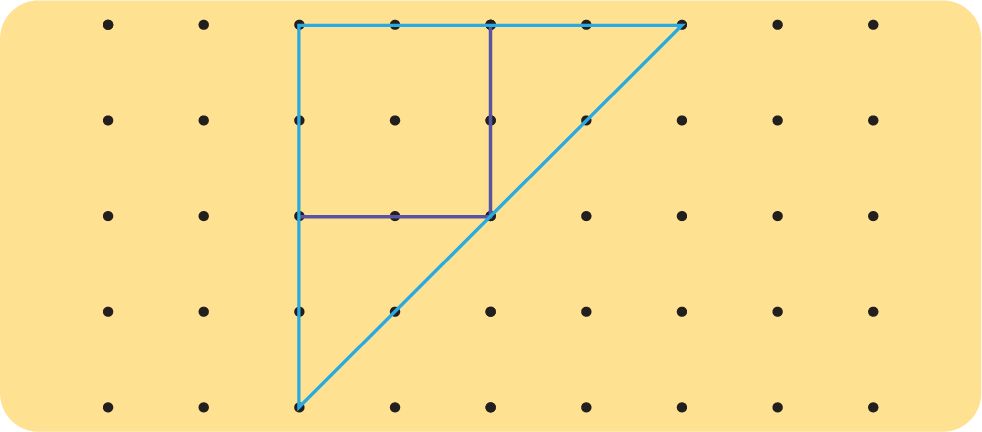
3. Draw 2 lines to divide the square into 3 triangles.

See AnswerYou can:
Draw 1 diagonal from top-left to bottom-right
Draw another line from bottom-left to the midpoint of the top side

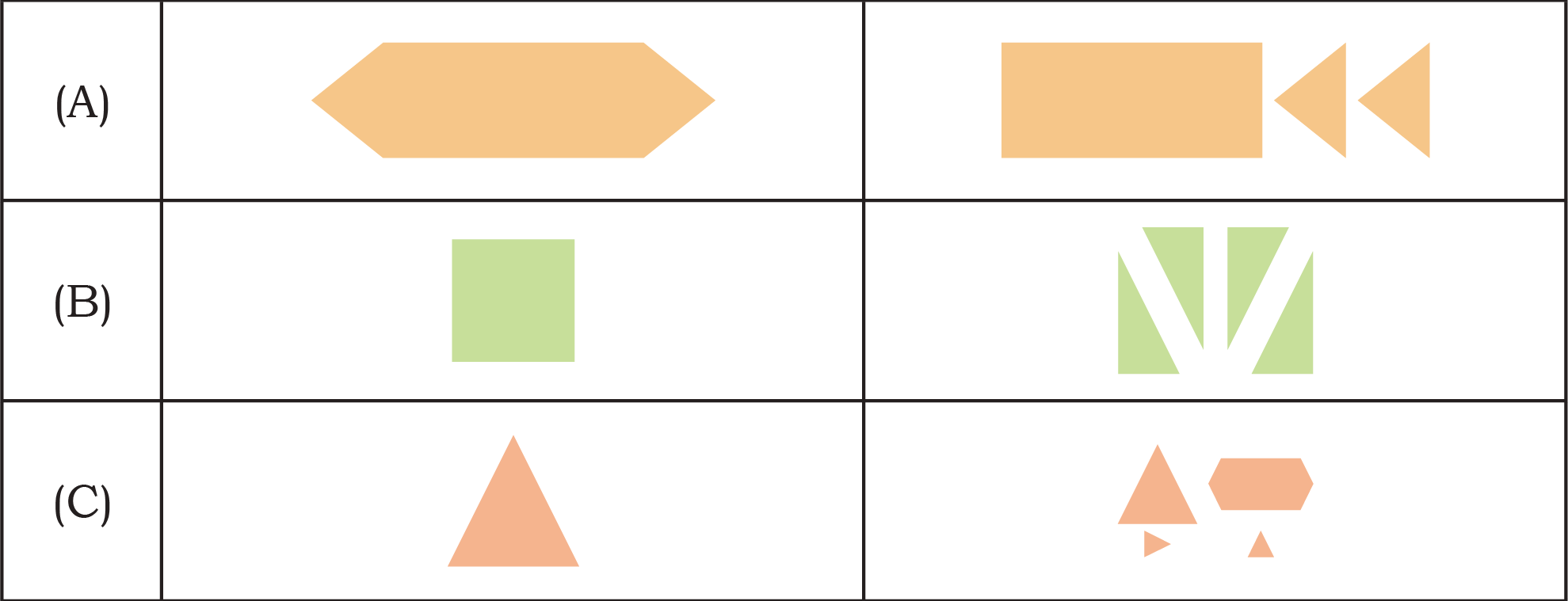
4. Draw lines to show the cuts needed on the shapes in the left column to get the smaller shapes on the right.

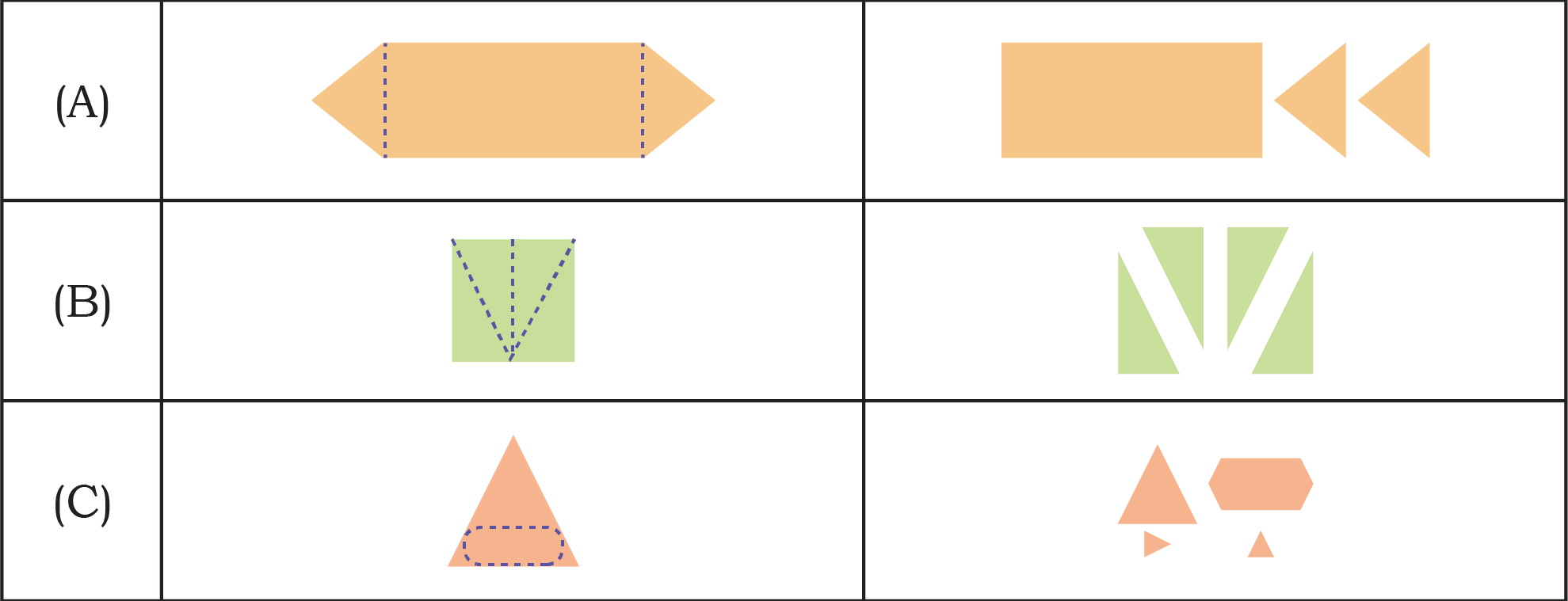
See AnswerThis is a practical activity requiring drawing specific cut lines on the shapes.

Page 21

Let Us Try

1. Squiggly spiders
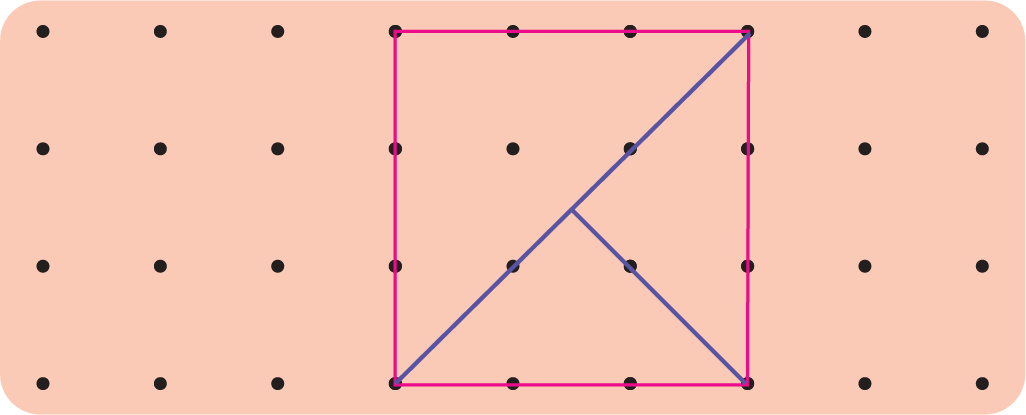
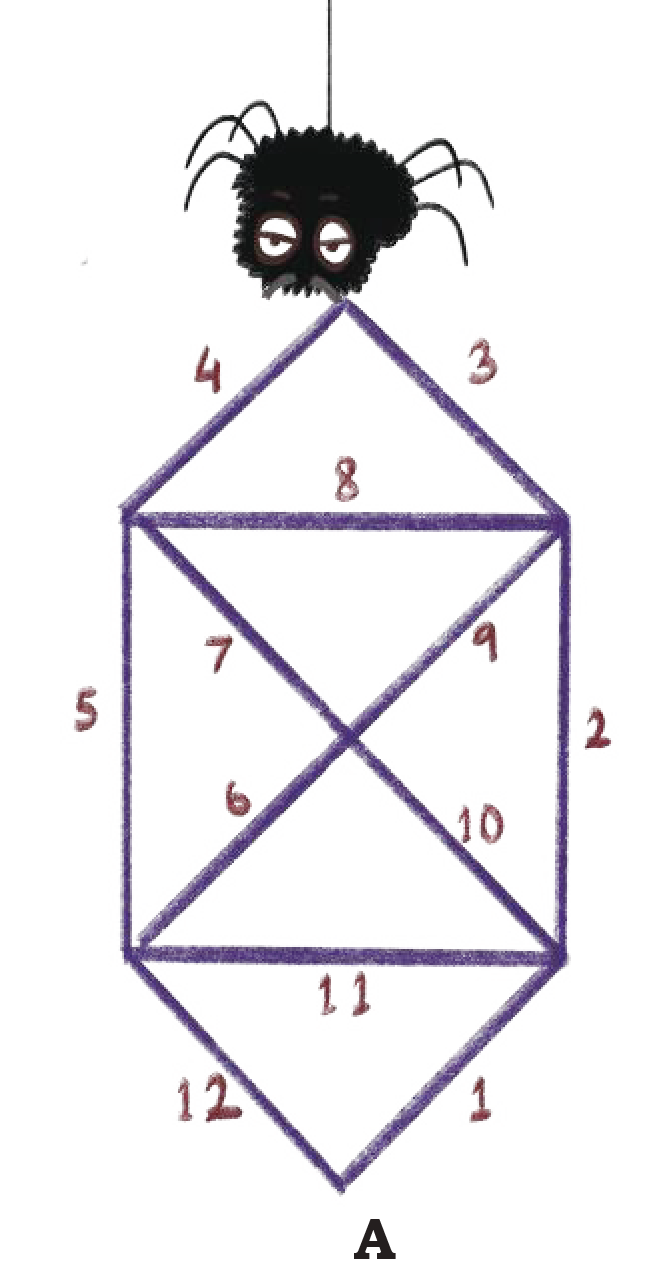
Squiggly, the spider, likes to make webs in different shapes. One day she begins to make triangular webs.
How many triangles are in her web?
See Answer6 triangles

She likes to take a walk each morning and check id the walls of her web are strong.
Can she begin at point A and reach back to the same point without walking on any wall more than once?
See AnswerYes, if she follow the web like 1, 2, 3, 4, 5, …, 11, 12.
Her brother, Wiggly made a web using rectangles.

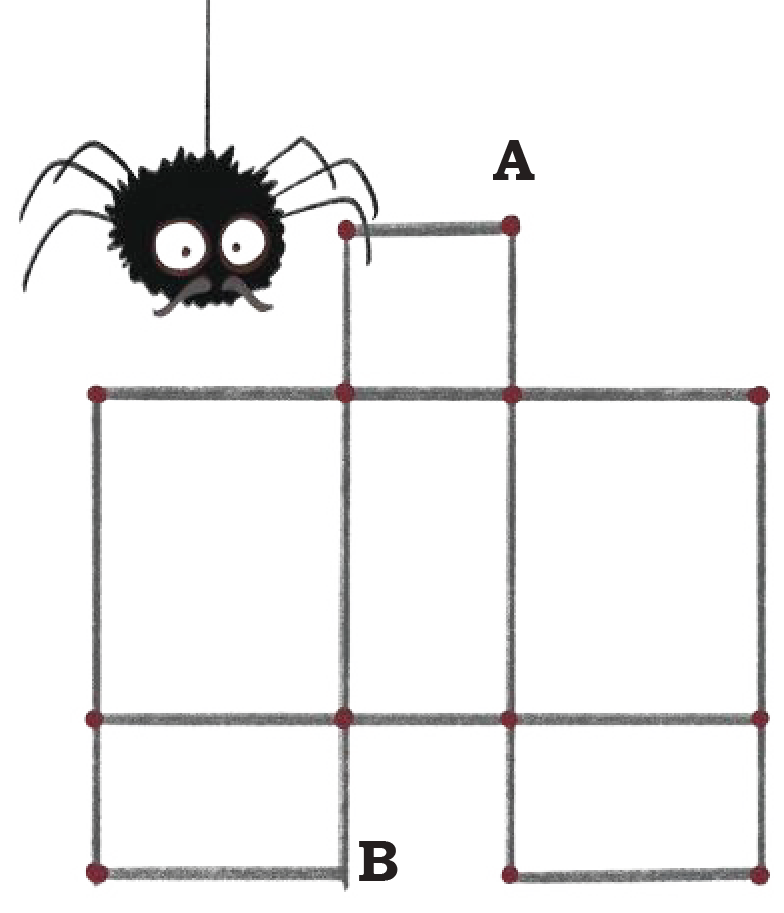
How many rectangles can you see in his web?
See AnswerThere are 6 rectangles.

Can he begin at point A and leave from point B without walking on any wall more than once?
See AnswerYes, he can!
A possible path:
A → right → down → left → down → right → B
(No wall is repeated.)
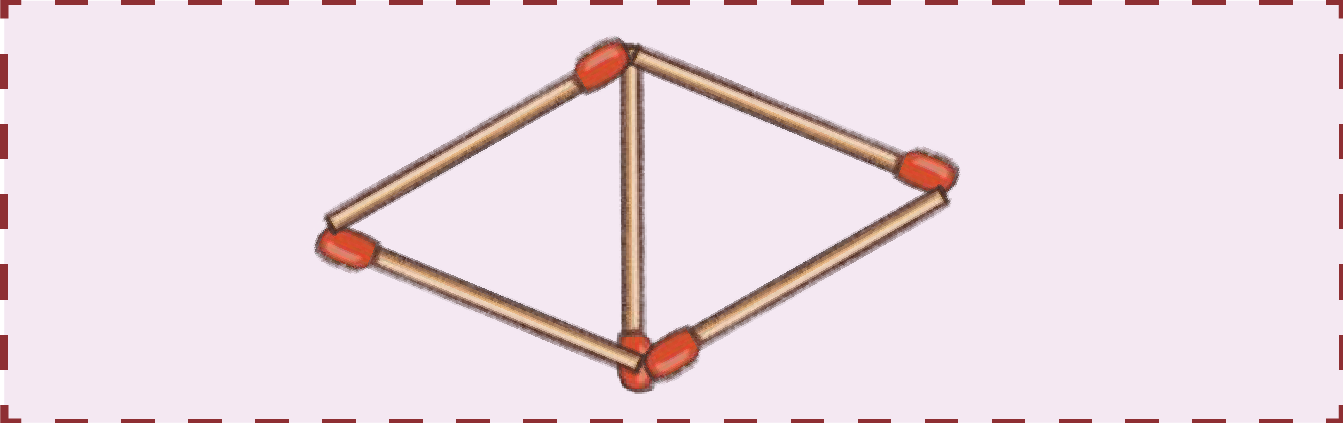
2. Use 5 matchsticks to make 2 triangles. Then draw it in the space provided.

See AnswerHere’s how you can do it:
Make one big triangle using 3 matchsticks.
Use the remaining 2 matchsticks to make a smaller triangle inside or beside the big one, sharing one side.
This forms 2 triangles using only 5 matchsticks.

3. Move two matchsticks to make 4 triangles.

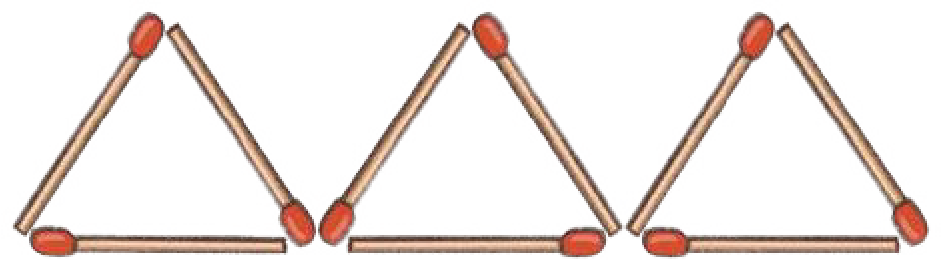
See AnswerForm a small triangle inside one big triangle.
(So now 1 big triangle is made up of 3 small ones + 1 big one = 4 triangles.)

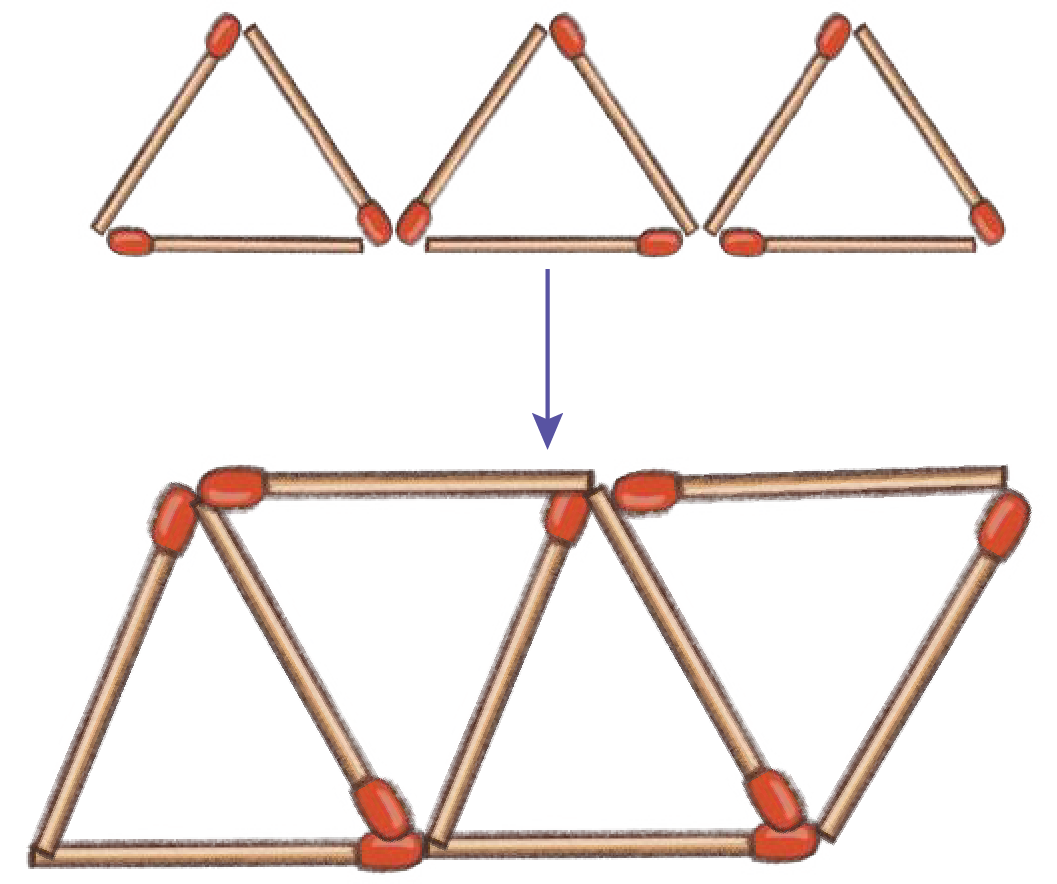
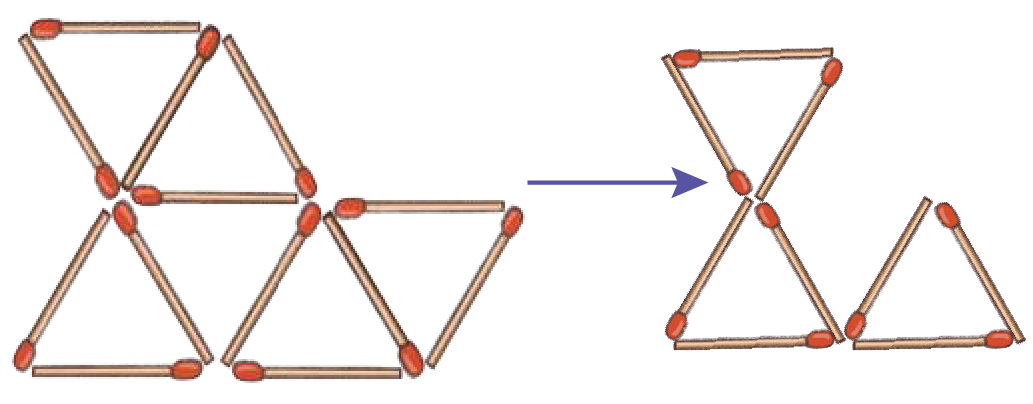
4. Remove 4 matchsticks to leave only 3 triangles

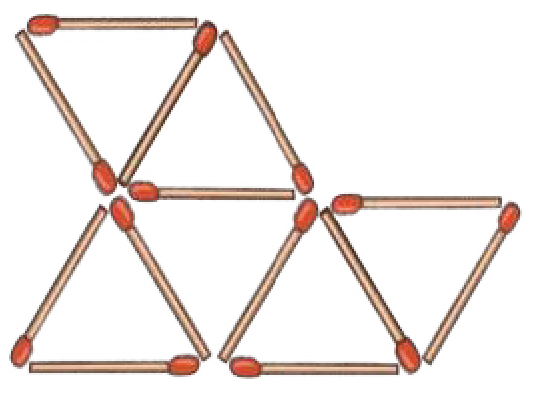
See AnswerRemove the top triangle and one side of a triangle on the bottom row.
Now, only 3 connected triangles will remain.

5. Model Challenge

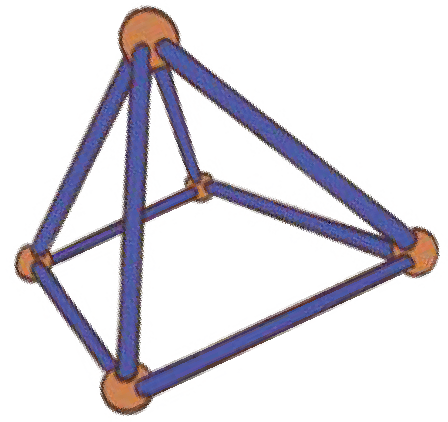
Can you make a model of solid shapes which has
a)12 straws and 8 clay balls?

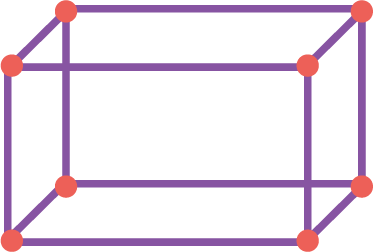
See AnswerYes, you can make a cube
b) 9 straws and 6 clay balls?

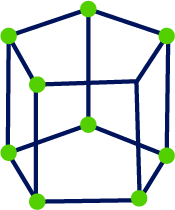
See AnswerYes, a triangular prism or pyramid
c) 15 straws and 10 clay balls?

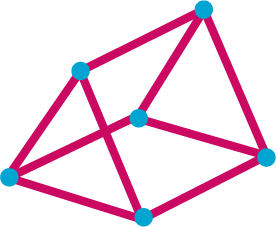
See AnswerYes, for example, a pentagonal shape
d) 10 straws and 6 clay balls?

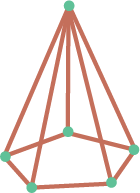
See AnswerYes, a square pyramid
6. Classify these shapes based on the number of angles.

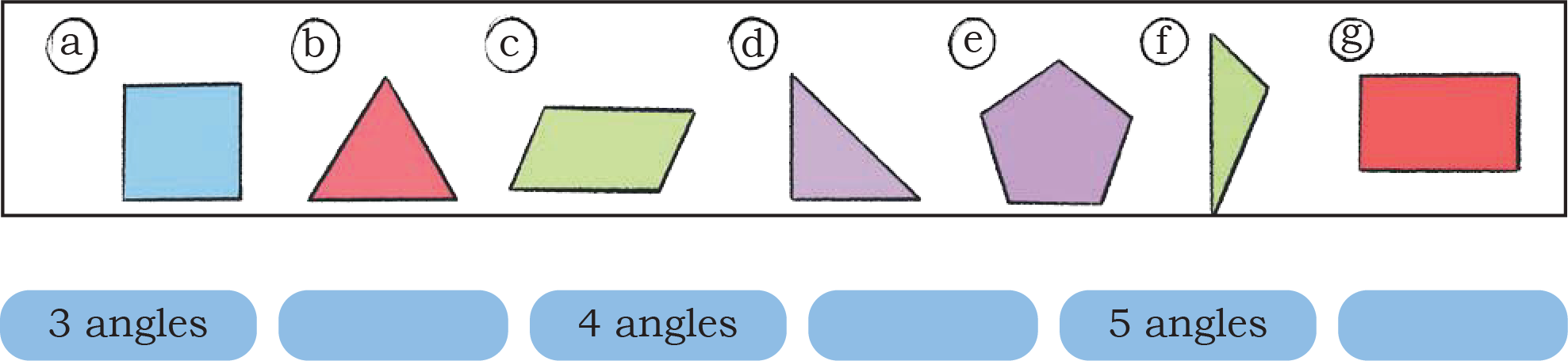
What relation do you notice between the number of sides and the number of angles?
See Answer3 angles: b, d, f
4 angles: a, c, g
5 angles: e
The number of angles = number of sides in each shape!

7. Draw a 2D shape that has less than 5 angles.
Draw a 2D shape with more than 5 angles.

See Answer2D Shapes with less than 5 angles: Triangle (3 angles) or quadrilateral (4 angles) – students would draw one of these.
2D Shapes with more than 5 angles: Hexagon, heptagon, octagon, etc. (student drawing)

8. Mark the right angles and write the number of right angles in each figure.

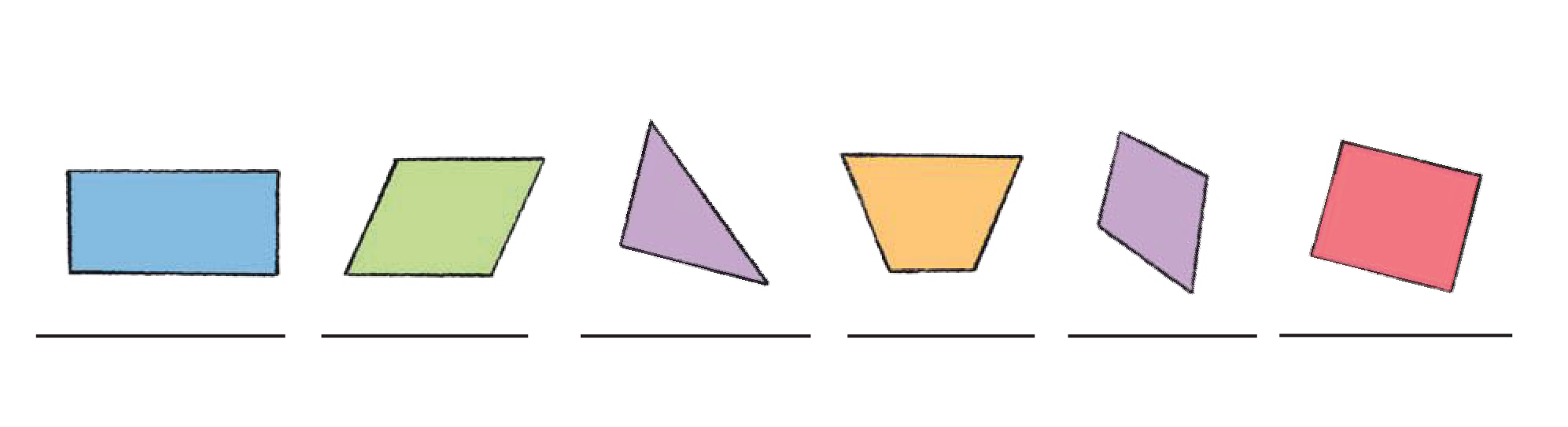
See Answer1st shape (blue rectangle): 4 right angles
2nd shape (green parallelogram): 0 right angles
3rd shape (purple triangle): 1 right angle
4th shape (yellow quadrilateral): 1 right angle
5th shape (violet irregular): 1 right angle
6th shape (red square): 4 right angles

Which shapes have only right angles?
See AnswerRectangle (1st shape) and Square (6th shape)
9. Observe the shapes and answer

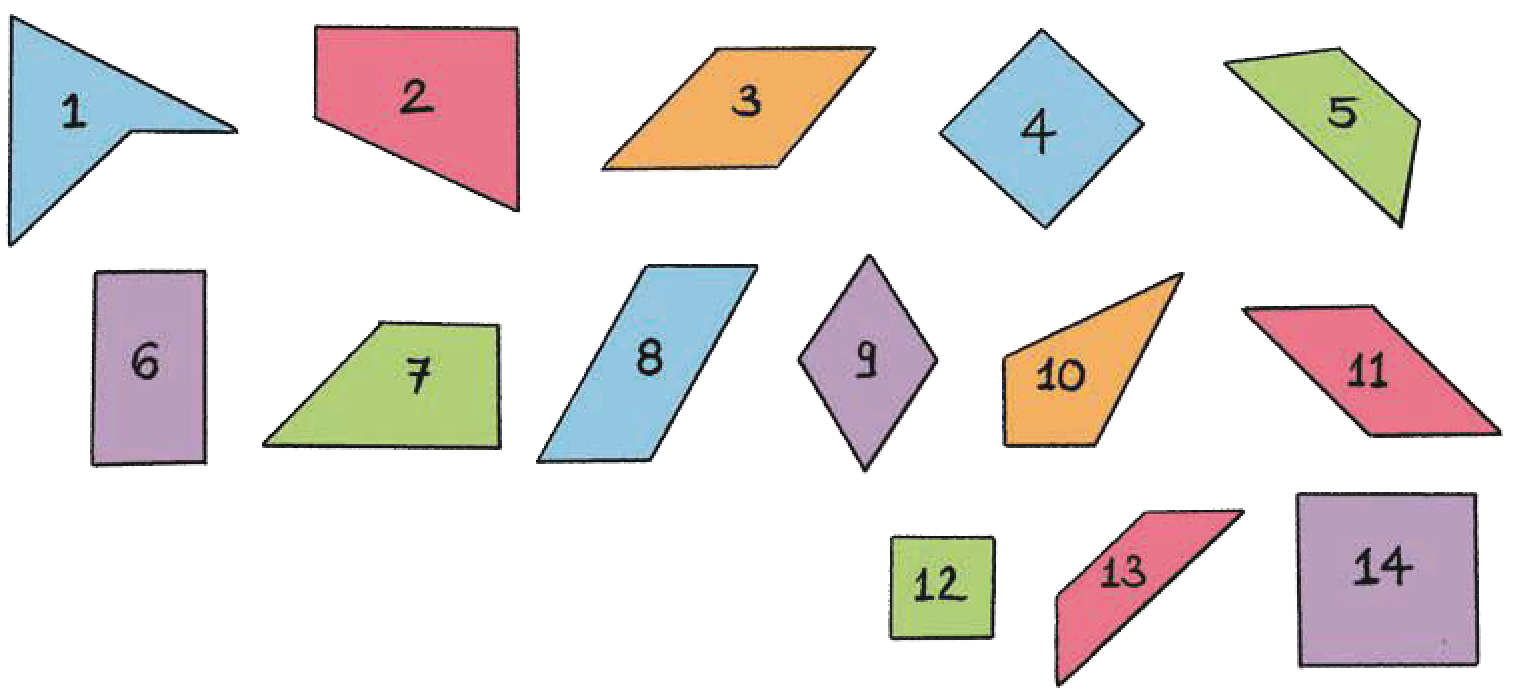
See Answer1. 2 right, 1 acute, 1 obtuse → Shape 14
2. 1 right, 2 obtuse, 1 acute → Shape 2
3. 2 obtuse, 2 acute → Shape 13
4. 4 right angles → Shape 6

These place is one of the major attractions for such things because in such places you are not only learning things you can have family time and also play. When you visit look around the fort and check each and every walls that has been created there. Then think about the yourself when you don’t know about the answer of some of the question.

In the book also you will found the designs with the help of bricks because in that time they did not have such types of tiles but that did not stop them because they had still made the designs that is not only looks beautiful but also functional and gave this structure strength.

If you haven’t get the idea how they do it or if you missed such walls and floors. You can check the designs in the picture of this chapter. You will found now the new designs and everything replaced this art but the inspiration is still taken from the designs that are done in the past not year of 10 years but more than 300 years ago. This chapter will teach you something that you have done in the past about the shapes and with shapes the design you can create.