by Tiwari Academy
NCERT Solutions for Class 4 Maths Chapter 10 Play with Patterns in English and Hindi Medium free to use online without any login or password. All the contents are updated according to new CBSE Syllabus 2024-25. NCERT books ensure that you are learning the subject in an interesting way. Class 4 Maths Chapter 10 does this by presenting you with patterns. By identifying patterns, it will help you in developing your analysis skills.
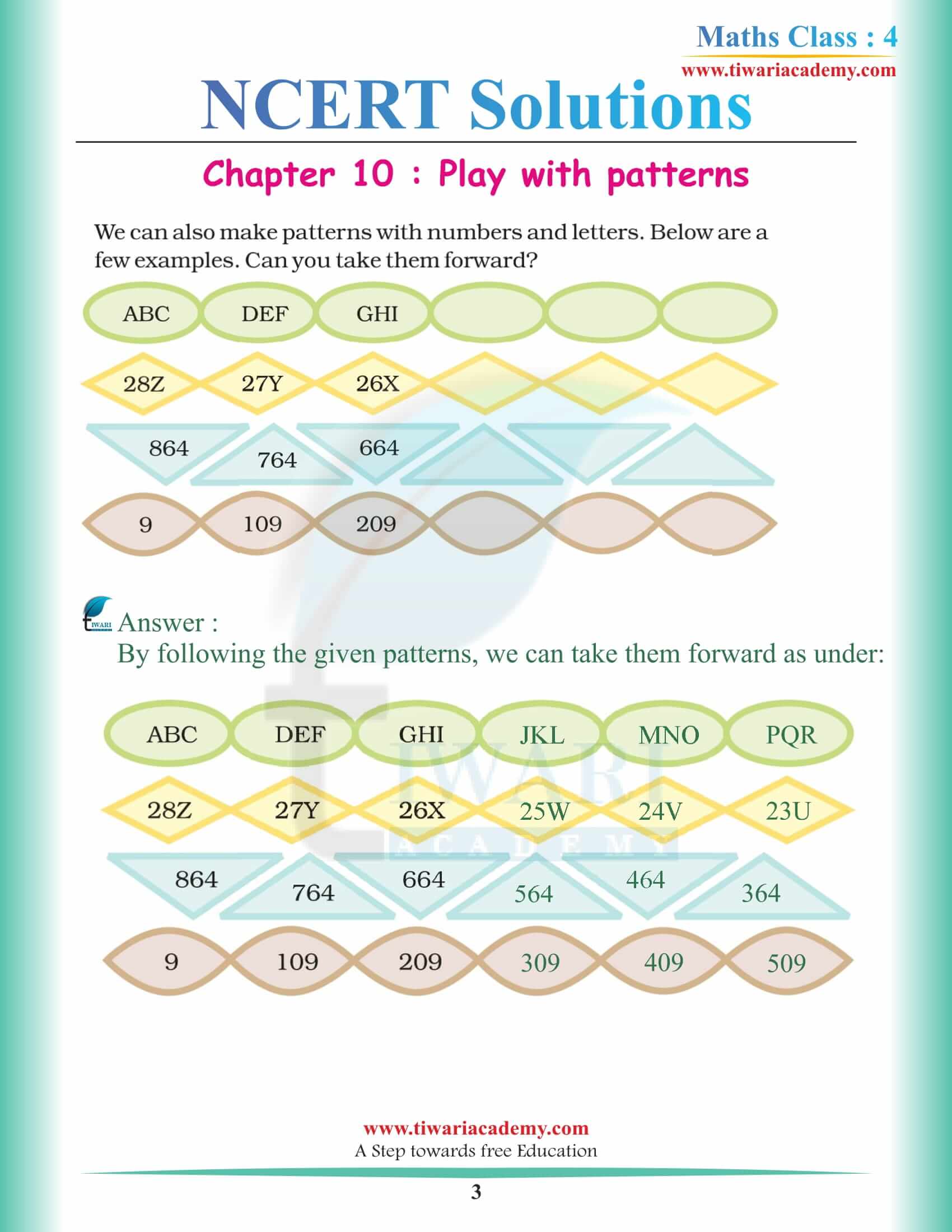
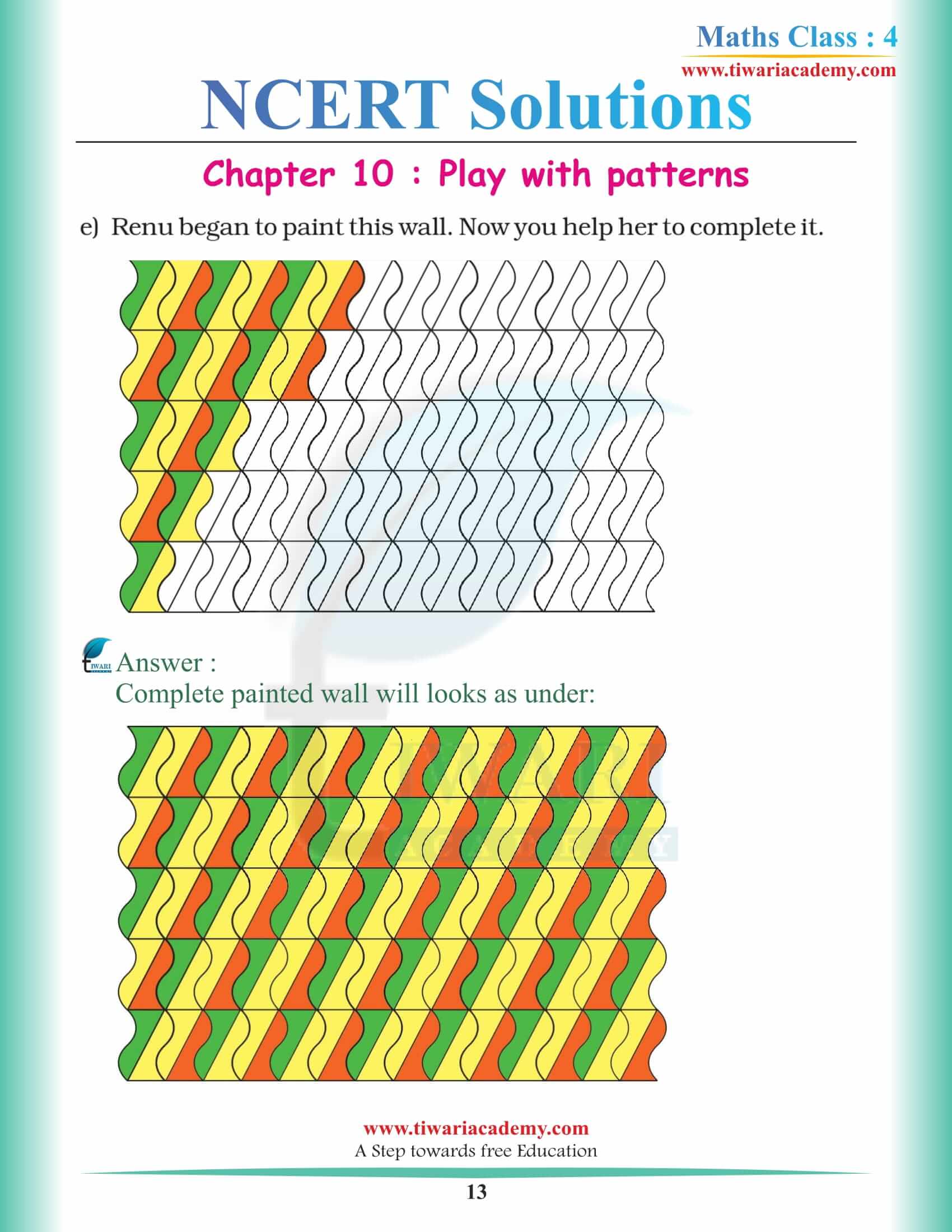
NCERT Solutions for Class 4 Maths Chapter 10 Play with Patterns
NCERT Solutions for Class 4 Maths Chapter 10
Download CBSE App Class 4
Class 4 NCERT Maths Chapter 10 Use of Patterns
We have already studied to make the patterns and how the patterns look like and what are the places where we can look for the patterns and now the question is where we can use the patterns?
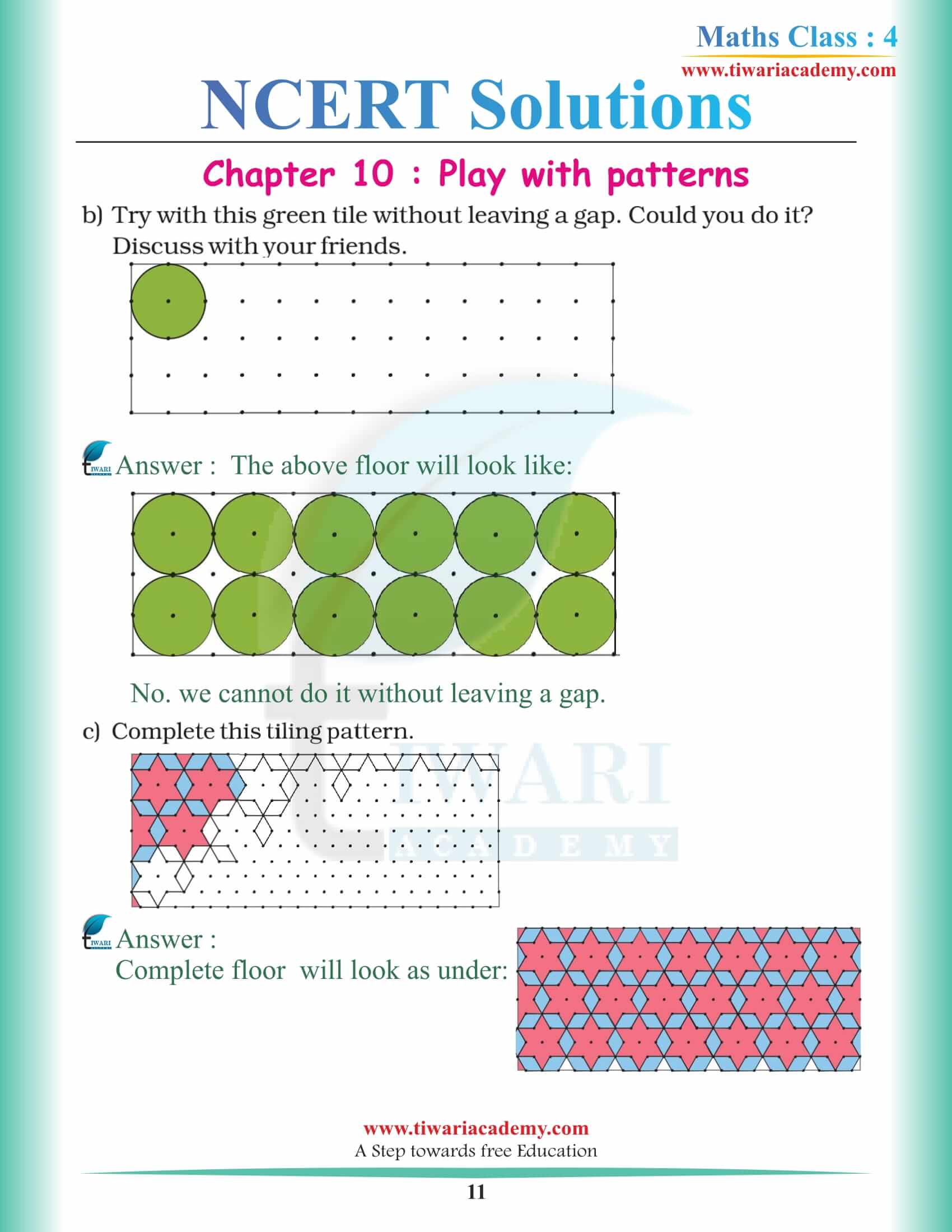
Well, I can answer this question in one Word. Everywhere! You can look around you and you will see even the clothes you are wearing contains patterns and Saree that your teacher is wearing right now much have patterns. Now the thing is to remember is that pattern does not necessarily contain big prints only some plain are also patterns. Anything that justifies its design we can call it a pattern. Now the point is how and where you want to draw these patterns. You will see the patterns on the wall of your home and you can spot it even where no one is looking on the wheels of your car and maybe on the tire.
CBSE Class 4 NCERT Maths Chapter 10 Fun with Patterns
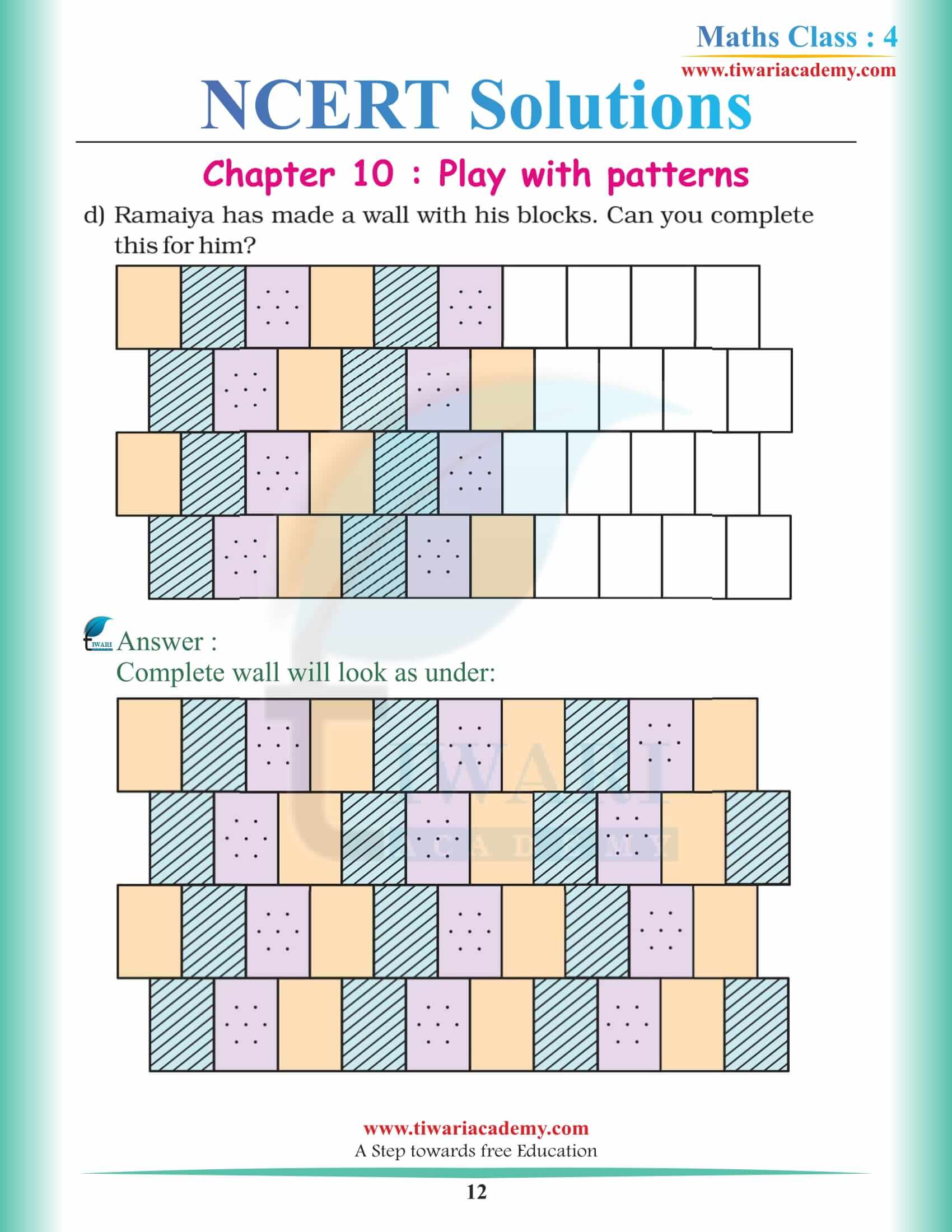
This is how you can find the patterns but how can you use the patterns to make fun is another interesting topic to discuss in the chapter you will learn how to make the fun stuff that can make you wonder how does that happen and how amazing it is. So if you want to know where and how you can implement the designs in your work you can study the chapter because it is important to understand how that pattern worked before you start making one yourself.
4th Standard NCERT Maths Chapter 10 Pattern Design on Saree
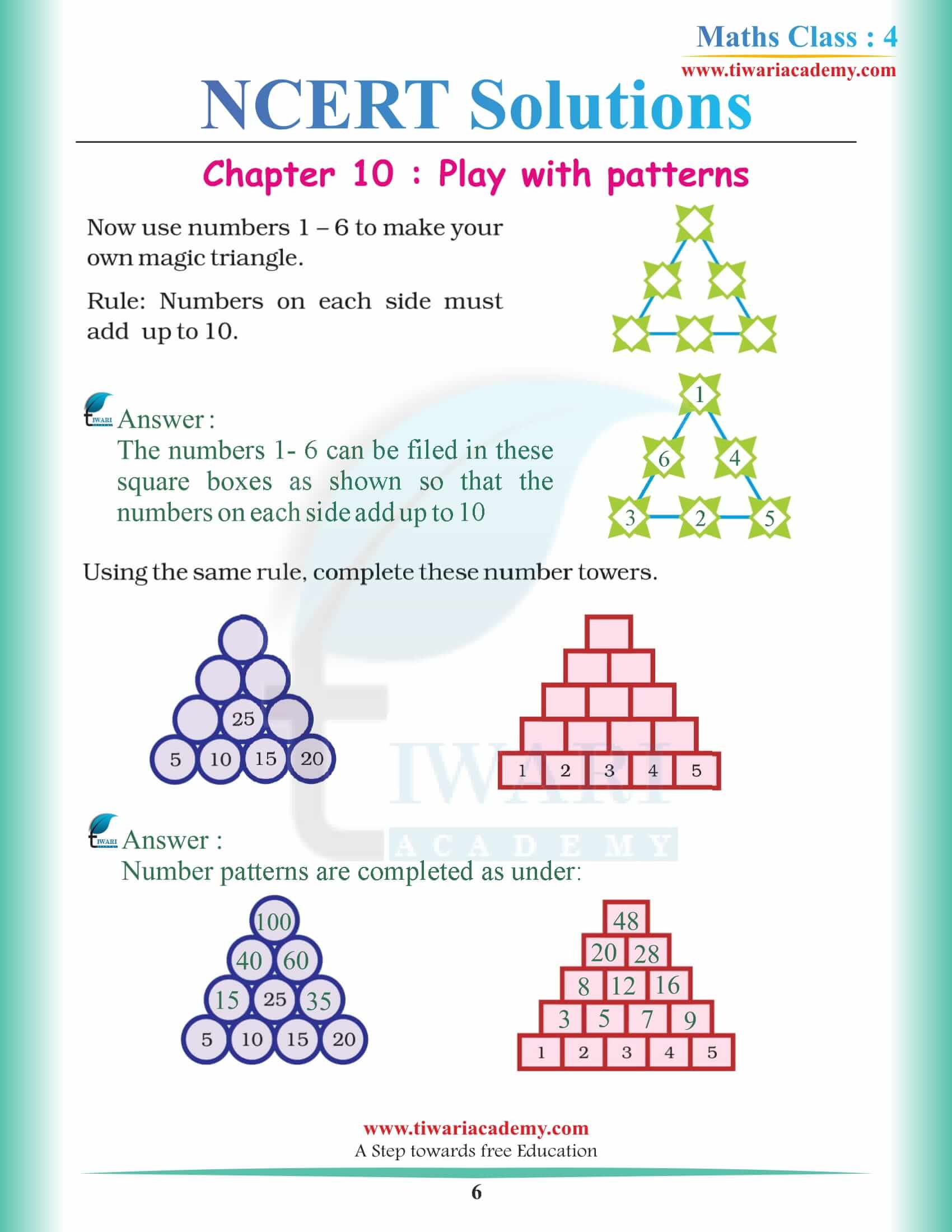
Like the other kid in the chapter, Raju started to make a Saree. Number Tower and Magic triangles are one of the designs with numbers are beings set up in such a way so that not only you can use it to make a number that can give you one desired result irrespective of the fact the number and design you choose under the result.
Class 4 NCERT Maths Textbook Chapter 10 Activity
Can you make some designs that are not given in the chapter and you can show them to your friends and amaze them with the results?
Class 4 NCERT Maths Book Chapter 10 Coding and Decoding
Coding and decoding secret messages is also a part of recognizing patterns. Recognizing rules is important for the development of mathematical thinking.
In unit 10 what students of class 4th will be able to learn?
In unit 10 students will be able to learn different types of patterns and shapes and how to use them in designs. Basically, this chapter is an advanced form of what the students of class 4th math already learned in the previous chapters.
How do you suggest students of class 4th Maths cover chapter 10?
I think the best way to understand the core knowledge of class is to learn through preparing the designs through the patterns to understand how the shapes are like. This will develop the understanding of shapes and how to name them so that they can use the knowledge to solve the question.
Do you think the students of class 4th Mathematics can cover unit 10 themselves?
The knowledge given in unit 10 is about shapes and students will get an opportunity to develop creativity. However, instruction and guidance is something that is required because not all students have the same developed understanding.
