NCERT Textbook Solutions for Class 10 Maths Chapter 2 Polynomials Updated for Session 2025-26 in Hindi and English Medium. To ensure a proper knowledge about the concepts, practice with Class 10 Maths Chapter 2 based Previous Year Board Questions Solutions given here as new addition.
Class 10 Maths Chapter 2 Solutions
Class 10 Maths Exercise 2.1
1. The graphs of y = p(x) are given in following figure, for some polynomials p(x). Find the number of zeroes of p(x), in each case.
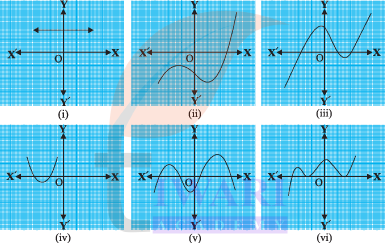
See Answer(i) The number of zeroes is 0 as the graph does not cut the x-axis at any point.
(ii) The number of zeroes is 1 as the graph intersects the x-axis at only 1 point.
(iii) The number of zeroes is 3 as the graph intersects the x-axis at 3 points.
(iv) The number of zeroes is 2 as the graph intersects the x-axis at 2 points.
(v) The number of zeroes is 4 as the graph intersects the x-axis at 4 points.
(vi) The number of zeroes is 3 as the graph intersects the x-axis at 3 points.
Class 10 Maths Chapter 2 Board Questions
Class 10 Maths Chapter 2 Assertion Reason Questions
Class 10 Maths Chapter 2 Case Study Based Questions
Class 10 Maths Exercise 2.2
1. Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients.
(i). x² – 2x – 8
See Answer(i) x² – 2x – 8
= x² – 4x + 2x – 8
= x(x – 4) + 2(x – 4)
= (x + 2)(x – 4)
The value of x² – 2x – 8 is zero if x + 2 = 0 or x – 4 = 0
=> x = -2 or x = 4
Therefore, the zeroes of x² – 2x – 8 are -2 and 4.
Now, Sum of zeroes
= -2 + 4 = 2
= -(-2)/1 = -(Coefficient of x)/Coefficient of x²
Product of zeroes = (-2) x 4 = -8
= -8/1 = Constant term/Coefficient of x²
(ii). 4s² – 4s + 1
See Answer(ii) 4s² – 4s + 1
= 4s² – 2s – 2s + 1
= 2s(2s – 1) – 1(2s – 1)
= (2s – 1)(2s – 1)
The value of 4s² – 4s + 1 is zero if 2s – 1 = 0
=> s = 1/2
Therefore, the zeroes of 4s² – 4s + 1 are 1/2 and 1/2.
Now, Sum of zeroes = 1/2 + 1/2 = 1
= -(-4)/4 = -(Coefficient of s) / Coefficient of s²
Product of zeroes = 1/2 x 1/2 = 1/4
= 1/4 = Constant term / Coefficient of s²
(iii). 6x² – 3 – 7x
See Answer(iii) 6x² – 3 – 7x
= 6x² – 7x – 3
= 6x² – 9x + 2x – 3
= 3x(2x – 3) + 1(2x – 3)
= (3x + 1)(2x – 3)
The value of 6x² – 7x – 3 is zero if 3x + 1 = 0 or 2x – 3 = 0.
=> x = -1/3 or x = 3/2.
Therefore, the zeroes of 6x² – 7x – 3 are -1/3 and 3/2.
Now, Sum of zeroes = -1/3 + 3/2
= (-2 + 9)/6 = 7/6 = -(-7)/6
= -(Coefficient of x) / Coefficient of x²
Product of zeroes = -1/3 x 3/2 = -1/2
= Constant term / Coefficient of x²
(iv). 4u² + 8u
See Answer(iv) 4u² + 8u
= 4u(u + 2)
The value of 4u² + 8u is zero if 4u = 0 or u + 2 = 0.
⇒ u = 0 or u = -2.
Therefore, the zeroes of 4u² + 8u are 0 and -2.
Now, Sum of zeroes = 0 + (-2) = -2
= -8/4 = -(Coefficient of u) / Coefficient of u²
Product of zeroes = 0 × (-2) = 0 = 0/4
= Constant term / Coefficient of u²
(v). t² – 15
See Answer(v) t² – 15
= t² – (√15)² = (t + √15)(t – √15)
The value of t² – 15 is zero if t + √15 = 0 or t – √15 = 0.
⇒ x = -√15 or x = √15.
Therefore, the zeroes of t² – 15 are -√15 and √15.
Now, Sum of zeroes = -√15 + √15 = 0 = -(0)/1
= -(Coefficient of t) / Coefficient of t²
Product of zeroes = (-√15) × √15 = -15 = -15/1
= Constant term / Coefficient of t²
(vi). 3x² – x – 4
See Answer(vi) 3x² – x – 4
= 3x² – 4x + 3x – 4
= x(3x – 4) + 1(3x – 4)
= (3x – 4)(x + 1)
The value of 3x² – x – 4 is zero if 3x – 4 = 0 or x + 1 = 0.
⇒ x = 4/3 or x = -1.
Therefore, the zeroes of 3x² – x – 4 are 4/3 and -1.
Now, Sum of zeroes = 4/3 + (-1) = (4 – 3)/3 = 1/3
= -(-1)/3 = -(Coefficient of x) / Coefficient of x²
Product of zeroes = 4/3 × (-1) = -4/3 = -4/3
= Constant term / Coefficient of x²
2. Find a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively.
(i). 1/4, -1
See Answer(i) Let α and β are the zeroes of the polynomial ax² + bx + c, then we have
α + β = 1/4 = -b/a
αβ = -1 = -4/4 = c/a
On comparing,
a = 4, b = -1 and c = -4
Hence, the required quadratic polynomial is 4x² – x – 4.
(ii). √2, 1/3
See Answer(ii) Let α and β are the zeroes of the polynomial ax² + bx + c, then we have
α + β = √2 = 3√2 / 3 = -b/a
αβ = 1/3 = c/a
On comparing,
a = 3, b = -3√2 and c = 1
Hence, the required quadratic polynomial is 3x² – 3√2x + 1.
(iii). 0, √5
See Answer(iii) Let α and β are the zeroes of the polynomial ax² + bx + c, then we have
α + β = 0 = 0/1 = -b/a
αβ = √5 = √5/1 = c/a
On comparing,
a = 1, b = 0 and c = √5
Hence, the required quadratic polynomial is x² + 0.x + √5
Hence, the required quadratic polynomial is x² + √5.
(iv). 1, 1
See Answer(iv) Let α and β are the zeroes of the polynomial ax² + bx + c, then we have
α + β = 1 = 1/1 = -b/a
αβ = 1 = 1/1 = c/a
On comparing,
a = 1, b = -1 and c = 1
Hence, the required quadratic polynomial is x² – x + 1.
(v). -1/4, 1/4
See Answer(v) Let α and β are the zeroes of the polynomial ax² + bx + c, then we have
α + β = -1/4 = -b/a
αβ = 1/4 = c/a
On comparing,
a = 4, b = 1 and c = 1
Hence, the required quadratic polynomial is 4x² + x + 1.
(vi). 4, 1
See Answer(vi) Let α and β are the zeroes of the polynomial ax² + bx + c, then we have
α + β = 4 = 4/1 = -b/a
αβ = 1 = 1/1 = c/a
On comparing,
a = 1, b = -4 and c = 1
Hence, the required quadratic polynomial is x² – 4x + 1.
Board Questions of Class 10 Maths Chapter 2 Polynomials
Board Exams Past Years Questions Based on Class 10 Maths Chapter 2 are given here with complete explanation and solutions. These Previous Years Exams Questions help the students to understand the pattern of Board Paper.
Chapter 2 MCQ Solutions
Class 10 Maths Chapter 2 Previous Year Questions
1. α and β are zeros of a quadratic polynomial px² + qx + 1. Form a quadratic polynomial whose zeros are 2/α and 2/β. [CBSE 2025]
See AnswerIf α and β are the zeros of px² + qx + 1, then: px² + qx + 1 = p(x – α)(x – β)
Now, we need to form a quadratic polynomial with zeros 2/α and 2/β.
Let’s say the new polynomial is f(x) = a(x – 2/α)(x – 2/β)
We can expand this: f(x) = a(x² – 2x/α – 2x/β + 4/αβ) = a[x² – 2x(1/α + 1/β) + 4/αβ]
We know that:
Sum of zeros of original polynomial: α + β = -q/p
Product of zeros of original polynomial: αβ = 1/p
Therefore:
1/α + 1/β = (α + β)/αβ = (-q/p)/(1/p) = -q
1/αβ = p
So our new polynomial is:
f(x) = a[x² – 2x(-q) + 4p]
= a[x² + 2qx + 4p]
This can be simplified to:
f(x) = ax² + 2aqx + 4ap
Taking a = 1 for simplicity, our answer is:
f(x) = x² + 2qx + 4p.
2. A teacher asked 10 of his students to write a polynomial in one variable on a paper and then to handover the paper. The following were the answers given by the students: 2x + 3, 3x² + 7x + 2, 4x³ + 3x² + 2, x³ + √3x + 7,
7x + √7, 5x³ – 7x + 2, 2x² + 3 – 5/x, 5x – 1/2, ax³ + bx² + cx + d, x + 1/x
Answer the following questions:
(i) How many of the above ten, are not polynomials?
(ii) How many of the above ten, are quadratic polynomials? [CBSE 2020]
See Solution(i) To identify non-polynomials, I need to check which expressions contain negative exponents, radicals with variables, or rational expressions with variables in the denominator.
Non-polynomials:
x³ + √3x + 7 (contains √3x, which has a variable under a radical)
7x + √7 (√7 is just a constant, so this is a polynomial)
2x² + 3 – 5/x (contains -5/x, which has a negative exponent x⁻¹)
5x – 1/2 (1/2 is just a constant, so this is a polynomial)
x + 1/x (contains 1/x, which has a negative exponent x⁻¹)
Therefore, 3 expressions are not polynomials: x³ + √3x + 7, 2x² + 3 – 5/x, and x + 1/x.
(ii) Quadratic polynomials have a degree of exactly 2.
Quadratic polynomials:
3x² + 7x + 2 (degree 2)
2x² + 3 – 5/x (not a polynomial)
Therefore, only 1 expression is a quadratic polynomial: 3x² + 7x + 2.
3. Find the zeroes of the quadratic polynomial x² – 15 and verify the relationship between the zeroes and the coefficients of the polynomial. [CBSE 2024]
See Solution Given polynomial: x² – 15
Step 1: Find the zeroes by setting the polynomial equal to zero. x² – 15 = 0 x² = 15 x = ±√15 So the zeroes are α = √15 and β = -√15
Step 2: Verify the relationship between zeroes and coefficients. For a quadratic polynomial ax² + bx + c, if α and β are the zeroes:
Sum of zeroes = α + β = -b/a
Product of zeroes = α × β = c/a
In our polynomial x² – 15, a = 1, b = 0, c = -15
Sum of zeroes: α + β = √15 + (-√15) = 0 = -b/a = -0/1 = 0
Product of zeroes: α × β = √15 × (-√15) = -15 = c/a = -15/1 = -15
The relationships are verified.
4. Find a quadratic polynomial whose zeroes are reciprocals of the zeroes of the polynomial f(x) = ax² + bx + c, a ≠ 0, c ≠ 0. [CBSE 2020]
See SolutionLet the zeroes of f(x) = ax² + bx + c be α and β.
Step 1: Find the reciprocals of these zeroes. The reciprocals are 1/α and 1/β.
Step 2: Form a quadratic polynomial with zeroes 1/α and 1/β. If g(x) is the new polynomial with zeroes 1/α and 1/β, then: g(x) = k(x – 1/α)(x – 1/β) where k is a constant
Step 3: Simplify this expression. g(x) = k(x – 1/α)(x – 1/β) = k(x² – x/β – x/α + 1/(αβ)) = k(x² – x(α+β)/(αβ) + 1/(αβ))
Step 4: Use the relationships for f(x): For f(x) = ax² + bx + c:
α + β = -b/a
αβ = c/a
Step 5: Substitute these relationships. g(x) = k(x² – x(-b/a)/(c/a) + 1/(c/a)) = k(x² + bx/c + a/c) = (k/c)(cx² + bx + a)
Therefore, the required quadratic polynomial is g(x) = cx² + bx + a, which is f(x) with the coefficients reversed.
5. Find the value of k such that the polynomial x² – (k + 6)x + 2(2k – 1) has sum of its zeroes equal to half of their product. [CBSE 2019]
See SolutionGiven polynomial: x² – (k + 6)x + 2(2k – 1)
Step 1: Identify the coefficients. a = 1, b = -(k + 6), c = 2(2k – 1) = 4k – 2
Step 2: Express the sum and product of zeroes. Sum of zeroes = -b/a = -(-(k + 6))/1 = k + 6 Product of zeroes = c/a = (4k – 2)/1 = 4k – 2
Step 3: Apply the given condition – sum equals half of product. k + 6 = (4k – 2)/2 k + 6 = 2k – 1 k + 6 + 1 = 2k k + 7 = 2k 7 = k
Therefore, k = 7.
6. Find the zeroes of the quadratic polynomial 7y² – (11/3)y – 2/3 and verify the relationship between the zeroes and the coefficients. [CBSE 2019]
See SolutionGiven polynomial: 7y² – (11/3)y – 2/3
Step 1: Find the zeroes using the quadratic formula. a = 7, b = -11/3, c = -2/3
y = [-b ± √(b² – 4ac)]/2a y = [(11/3) ± √((11/3)² – 4(7)(-2/3))]/14 y = [(11/3) ± √(121/9 + 56/3)]/14 y = [(11/3) ± √(121/9 + 168/9)]/14 y = [(11/3) ± √(289/9)]/14 y = [(11/3) ± 17/3]/14 y = [11 ± 17]/42
The zeroes are: α = (11 + 17)/42 = 28/42 = 2/3 and β = (11 – 17)/42 = -6/42 = -1/7
Step 2: Verify the relationship between zeroes and coefficients. For a quadratic polynomial ay² + by + c, if α and β are the zeroes:
Sum of zeroes = α + β = -b/a
Product of zeroes = α × β = c/a
In our polynomial:
Sum of zeroes: 2/3 + (-1/7) = (14/21) + (-3/21) = 11/21 -b/a = -(-11/3)/7 = 11/21
Product of zeroes: (2/3) × (-1/7) = -2/21 c/a = (-2/3)/7 = -2/21
The relationships are verified.
Assertion-Reason Type Questions
(a) Both Assertion and Reason are true and Reason is the correct explanation of Assertion.
(b) Both Assertion and Reason are true but Reason is not the correct explanation of Assertion.
(c) Assertion is true but Reason is false.
(d) Assertion is false but Reason is true.
1. Assertion (A): Degree of a zero polynomial is not defined.
Reason (R): Degree of a non-zero constant polynomial is 0.
See Solution(a) Both the assertion and reason are true and the reason correctly explains the assertion.
The zero polynomial (0) has no defined degree in polynomial mathematics because it has no non-zero terms. Meanwhile, a non-zero constant polynomial (like 5 or -7) has degree 0. This distinction is part of why we need to treat the zero polynomial as a special case, which explains why its degree remains undefined.
2. Assertion (A): (2 – √3) is one zero of the quadratic polynomial then other zero will be (2 + √3).
Reason (R): Irrational zeroes always occurs in pairs.
See Solution(b) Both assertion and reason are true, but the reason is not the complete explanation for the assertion.
If (2 – √3) is one zero of a polynomial with real coefficients, then (2 + √3) must be another zero. This occurs due to the complex conjugate pair theorem, which states that if a polynomial has real coefficients, then complex roots (including irrational roots) occur in conjugate pairs. However, the reason given is not precise – it’s not that “irrational zeros always occur in pairs” in general, but specifically that when a polynomial has real coefficients, roots like (2 – √3) must have their conjugate (2 + √3) as another root.
3. Assertion (A): A quadratic polynomial having 4 and 3 as zeroes is x² – 7x + 12.
Reason (R): The quadratic polynomial having α and β as zeroes is given by P(x) = x² – (α + β)x + αβ.
See Solution(a) Both assertion and reason are true, and the reason correctly explains the assertion.
Using the formula P(x) = x² – (α + β)x + αβ where α=4 and β=3:
Sum of zeros: α + β = 4 + 3 = 7
Product of zeros: αβ = 4 × 3 = 12 Therefore P(x) = x² – 7x + 12, which confirms the assertion.
4. Assertion (A): If α and β are the zeroes of the polynomial x² + 2x – 15, then 1/α + 1/β is 2/15.
Reason (R): If α and β are the zeroes of a quadratic polynomial ax² + bx + c, then α + β = -b/a and αβ = c/a.
See Solution(a) Both assertion and reason are true, and the reason explains the assertion.
For the polynomial x² + 2x – 15, we have a=1, b=2, and c=-15. Using the given properties:
α + β = -b/a = -2/1 = -2
αβ = c/a = -15/1 = -15
To find 1/α + 1/β, we use the identity 1/α + 1/β = (α + β)/(αβ) Therefore, 1/α + 1/β = -2/(-15) = 2/15, confirming the assertion.
5. Assertion (A): If one zero of the polynomial P(x) = (k + 18)x² + 11x + 4k is the reciprocal of the other zero, then k = 6.
Reason (R): If (x – α) and (x – β) are the factors of the polynomial P(x), then α and β are the zeroes of P(x).
See Solution(b) Both assertion and reason are true, but the reason doesn’t explain the assertion.
Let’s solve for k where one zero is the reciprocal of the other. If the zeros are α and β where β = 1/α, then:
For ax² + bx + c with zeros α and β, we know α + β = -b/a and αβ = c/a
For polynomial P(x) = (k + 18)x² + 11x + 4k, we have a = k + 18, b = 11, c = 4k
If one zero is the reciprocal of the other, then αβ = 1
So c/a = 1, which means 4k/(k + 18) = 1
Solving: 4k = k + 18
3k = 18
k = 6
The reason provided is correct but doesn’t explain how to find k.
6. Assertion (A): If the zeroes of the polynomial f(x) = (k² + 4)x² + 4kx + (k³ – 9) are equal in magnitude but opposite in sign, then value of k is zero.
Reason (R): A quadratic polynomial whose zeroes are α and β is x² + (α + β)x + αβ.
See Solution(c) The assertion is true but the reason is false.
If zeros are equal in magnitude but opposite in sign, we have α = -β, which means α + β = 0. For a quadratic polynomial ax² + bx + c, we know α + β = -b/a
For the given polynomial f(x) = (k² + 4)x² + 4kx + (k³ – 9):
a = k² + 4
b = 4k
c = k³ – 9
Since α + β = 0, we need -b/a = 0, which means b = 0:
4k = 0
k = 0
The reason provided is incorrect.
The formula should be P(x) = x² – (α + β)x + αβ, not x² + (α + β)x + αβ.
7. Assertion (A): If m and n are the zeroes of the polynomial 3x² + 11x – 4, then 12(m² + n²) + 145mn = 0.
Reason (R): If α and β are the zeroes of the polynomial x² + bx + c, then α/β + β/α = b²/ac + 2.
See Solution(d) Both the assertion and reason are false.
For the polynomial 3x² + 11x – 4, we have a=3, b=11, c=-4. Using the relations for zeros:
m + n = -b/a = -11/3
mn = c/a = -4/3
Now, let’s check the assertion: 12(m² + n²) + 145mn We know that (m + n)² = m² + n² + 2mn So m² + n² = (m + n)² – 2mn = (-11/3)² – 2(-4/3) = 121/9 + 8/3 = 121/9 + 24/9 = 145/9
Therefore: 12(m² + n²) + 145mn = 12(145/9) + 145(-4/3) = 1740/9 – 580/3 = 1740/9 – 1740/9 = 0
The assertion is actually true.
The reason, however, is false.
The correct relation is α/β + β/α = (α + β)²/(αβ) – 2, not b²/ac + 2.
Since the assertion is true but the reason is false, the answer is (c).
8. Assertion (A): If one of the zeroes of the quadratic polynomial (k – 1)x² + kx + 1 is -3, then the value of k is 4/3.
Reason (R): If -1 is a zero of the polynomial P(x) = kx² – 4x + k, then the value of k is -2.
See Solution(b) Both assertion and reason are true, but the reason doesn’t explain the assertion.
For the assertion: If -3 is a zero of the polynomial (k – 1)x² + kx + 1, then: (k – 1)(-3)² + k(-3) + 1 = 0 (k – 1)(9) – 3k + 1 = 0 9k – 9 – 3k + 1 = 0 6k – 8 = 0 6k = 8 k = 4/3
The assertion is true.
For the reason: If -1 is a zero of P(x) = kx² – 4x + k, then: k(-1)² – 4(-1) + k = 0 k + 4 + k = 0 2k + 4 = 0 2k = -4 k = -2
The reason is also true, but it’s independent of the assertion and doesn’t explain it.
9. Assertion (A): If one zero of polynomial P(x) = (k² + 4)x² + 13x + 4k is reciprocal of other, then k = 2.
Reason (R): If (x – a) is a factor of p(x), then p(a) = 0, i.e., a is a zero of p(x).
See Solution(b) Both assertion and reason are true, but the reason does not explain the assertion.
For the assertion: Let the zeros be α and β where β = 1/α. For a polynomial ax² + bx + c with zeros α and β:
α + β = -b/a
αβ = c/a
If β = 1/α, then αβ = 1, which means c/a = 1.
For P(x) = (k² + 4)x² + 13x + 4k:
a = k² + 4
b = 13
c = 4k
Since αβ = 1, we have 4k/(k² + 4) = 1 4k = k² + 4 k² – 4k + 4 = 0 (k – 2)² = 0 k = 2
The assertion is true.
The reason is a basic property of polynomials that is generally true but doesn’t specifically explain why k = 2 in this particular case.
10. Assertion (A): If α, β, γ are the zeroes of x³ – 2x² + qx – r and α + β = 0, then 2q = r.
Reason (R): If α, β, γ are the zeroes of ax³ + bx² + cx + d, then α + β + γ = -b/a; αβ + βγ + γα = c/a; αβγ = -d/a.
See Solution(a) Both assertion and reason are true, and the reason correctly explains the assertion.
For a cubic polynomial ax³ + bx² + cx + d with zeros α, β, and γ:
α + β + γ = -b/a
αβ + βγ + γα = c/a
αβγ = -d/a
For the polynomial x³ – 2x² + qx – r, we have a=1, b=-2, c=q, d=-r.
α + β + γ = -b/a = -(-2)/1 = 2
αβ + βγ + γα = c/a = q/1 = q
αβγ = -d/a = -(-r)/1 = r
Given α + β = 0, and α + β + γ = 2, we get: γ = 2 – (α + β) = 2 – 0 = 2
From α + β = 0, we know αβ = -α² (substituting β = -α)
For αβ + βγ + γα: q = αβ + βγ + γα = -α² + (-α)(2) + (2)(α) = -α² – 2α + 2α = -α²
For αβγ: r = αβγ = αβ(2) = -α²(2) = -2α²
Therefore, q = -α² and r = -2α², which means r = 2q.
The reason correctly explains how to derive this relationship using the properties of cubic polynomial roots.
Case Based Type Questions
Case Study 1
In a pool at an aquarium, a dolphin jumps out of the water travelling at 20 cm/s. Its height above water level after t is given by h = 20t – 16t².
Based on the above information, answer the following questions. [CBSE 2023]
(i) Find zeroes of polynomial p(t) = 20t – 16t².
See SolutionTo find the zeroes, we need to solve p(t) = 0:
20t – 16t² = 0
16t² – 20t = 0
4t(4t – 5) = 0
Therefore, t = 0 or t = 5/4
The zeroes are 0 and 5/4 seconds.
(ii) Which of the following types of graph represent p(t)?
See SolutionThe polynomial p(t) = 20t – 16t² can be rewritten as p(t) = -16t² + 20t, which is a quadratic function with a negative leading coefficient.
This means it’s a parabola opening downward.
The zeros are at t = 0 and t = 5/4. The vertex occurs at t = -b/(2a) = -20/(-32) = 5/8, which is between 0 and 5/4. At t = 0, h = 0 and at t = 5/4, h = 0. At t = 5/8, the height is maximum.
Looking at the given graphs, option (a) correctly represents this polynomial, showing a parabola that:
Opens downward
Crosses the x-axis at t = 0 and t = 5/4
Has a maximum at approximately t = 5/8
Answer: (a)
(iii) (a). What would be the value of h at t = 3/2? Interpret the result. (b). How much distance has the dolphin covered before hitting the water level again?
See Solution(a). Substituting t = 3/2 into the equation h = 20t – 16t²: h = 20(3/2) – 16(3/2)² h = 30 – 16(9/4) h
= 30 – 36
h = -6
At t = 3/2 seconds, the height is -6 cm, which means the dolphin is 6 cm below the water level.
(b). The dolphin hits the water level again when h = 0, which occurs at t = 5/4 seconds (as we found in part i).
To find the horizontal distance covered, we need to multiply the horizontal velocity (20 cm/s) by the time (5/4 s):
Distance = 20 cm/s × 5/4 s = 25 cm
Therefore, the dolphin covered 25 cm horizontally before hitting the water level again.
Exercise 2.1 Solutions
Exercise 2.2 Solutions
For students seeking focused study sessions, downloadable resources such as Class 10 NCERT Maths Exercises Chapter 2 PDF are invaluable. Detailed explanations in Step-by-Step Solutions make even complex problems manageable. Revising topics through Class 10 Maths Chapter 2 Revision Notes ensures last-minute preparation is efficient. Mastering this chapter becomes easier with the right blend of practice, conceptual clarity and consistent revision. Class 10 NCERT Maths Solution is as per CBSE syllabus and NCERT Class 10 Maths books published for academic year 2025-26. There are only two exercises in Chapter 2 of class 10th Math Solution.
Class 10 Maths Chapter 2 NCERT Detailed Solutions
Class 10 Maths Chapter 2 Solutions for State Boards
Class 10 Maths Chapter 2 Polynomials, is an important topic in the NCERT Mathematics syllabus. Students often search for reliable NCERT Class 10 Math Explanation Guide Chapter 2 to be confident in the subject. 10th math textbook solutions cover all exercises, including Exercise 2.1, Exercise 2.2, Exercise 2.3 and Exercise 2.4, providing step-by-step answers to problems. Many students prefer downloadable NCERT Polynomials Solutions PDF for offline study and revision.
The chapter 2 explains fundamental concepts like the degree of polynomials, zeroes of polynomials and their graphical representation. To enhance their preparation, students can refer to 10th Maths NCERT Chapter 2 Important Questions, MCQ and CBSE Practice Questions. For quick revisions, Class 10 Maths Exercises Chapter 2 Notes and Revision Notes come in handy. Accessing Class 10 Maths NCERT Chapter 2 Video Lectures helps in better understanding through visual aids, making learning more engaging and effective.
Key Points for Class 10 Maths Chapter 2 Polynomials in Board Exams
Class 10 Maths Chapter 2 Polynomials, focuses on key concepts such as zeroes of polynomials, their relationship with coefficients, division algorithms and factorization techniques. Understanding graphical representation and solving polynomial equations is crucial. Practice exercises, MCQ and previous year questions ensure better preparation for board exams. Master problem-solving for high scoring.
| Day | Topics to Cover | Recommended Resources | Practice Tasks |
|---|---|---|---|
| Day 1 | Introduction to Polynomials, Degree of Polynomials | NCERT Textbook, Video Lectures | Solve Exercise 2.1 |
| Day 2 | Zeroes of Polynomials and Their Graphical Representation | NCERT Solutions PDF, Online Tutorials | Practice Graph-Based Problems |
| Day 3 | Relationship Between Zeroes and Coefficients | Revision Notes, Expert Solutions | Solve Exercise 2.2 |
| Day 4 | Division Algorithm for Polynomials | NCERT Textbook, Sample Papers | Solve Exercise 2.3 |
| Day 5 | Factorization of Polynomials | Video Lectures, Important Questions | Solve Exercise 2.4 |
| Day 6 | Revision and Concept Review | MCQs, Previous Year Questions | Attempt Online Tests |
Class 10 Maths Chapter 2 Polynomials explore various important concepts related to polynomial equations. Here are the main points to learn from this chapter. Understand what polynomials are and their characteristics. A polynomial is an algebraic expression consisting of variables, coefficients and exponents, with non-negative integer exponents. Learn how to determine the degree of a polynomial based on the highest power of the variable term. Identify polynomials as constant, linear, quadratic, cubic, etc., based on their degree.
The textbooks issued by NCERT shows that there are only two exercises in chapter 2 of 10th mathematics. So, students have to practice only exercise 2.1 and 2.2 for the board exams. According to new syllabus and books issued for new session, the course structure of class 10 chapter 2 is as follows:
Zeros of a polynomial. Relationship between zeros and coefficients of quadratic
polynomials.
1. Now, Number of Exercises: 2
2. Number of Periods needed: 8
3. Weightage of Maths: 4 – 5
Know how to add and subtract polynomials by combining like terms. Understand the process of multiplying polynomials using the distributive property. Learn how to use the FOIL method for binomial multiplication (First, Outer, Inner, Last). Multiply a monomial by a polynomial and apply the distributive property. Recognize and apply formulas for special products such as the square of a binomial (a + b)² and the difference of squares (a² – b²).
| Class: 10 | Mathematics |
| Chapter 2: | Polynomials |
| Number of Exercises: | 2 (Only Two) |
| Content: | Textbook and Extra Questions |
| Content Type: | Text, Images and Videos |
| Academic Session: | Year 2025-26 |
| Medium: | English and Hindi Medium |
Solutions for Class 10 Maths NCERT Chapter 2
UP board Students, who are using NCERT Textbooks for their final exams, they can download UP Board Solutions for Class 10 Maths Chapter 2 from this page in PDF format. Assignments and Revision tests are given below in the format of PDF file.
Study polynomial division using long division and synthetic division methods.
Understand the concepts of divisors, dividends, quotients, and remainders. Learn techniques for factoring polynomials, including common factors, grouping, and the use of algebraic identities. Factorize quadratic trinomials of the form ax² + bx + c.
Familiarize yourself with important algebraic identities, such as (a + b)², (a – b)², and a² – b². Understand the Remainder Theorem, which relates the remainder of polynomial division to the value of the polynomial at a given point. Know the Factor Theorem, which states that (x – a) is a factor of a polynomial if and only if the polynomial evaluates to zero at x = a.

Learn how to use synthetic division for polynomial division, particularly for dividing by linear divisors of the form (x – a). Apply polynomial equations to real-world problems and mathematical modeling. Solve polynomial equations, both linear and quadratic, by factoring and applying the zero-factor property. Understand the graphical representation of polynomial functions and how to find the roots or solutions by analyzing the graph.
According to real-time information, and the knowledge based on information available up to session 2025-26, we provide specific information about the availability of study materials for Class 10 Maths Chapter 2 Polynomials at Tiwari Academy website and Apps.
Summarize the key concepts, formulas, and techniques learned in this chapter for quick reference. These are the main points to learn from Class 10 Maths Chapter 2 Polynomials. It is a fundamental chapter in algebra that serves as a basis for more advanced topics in mathematics.
What are the important terms of 10th Maths Chapter 2 Polynomials?
What do you understand by a Polynomial as per Class 10 Maths Chapter 2?
An algebraic expression, in which variable(s) does (do) not occur in the denominator, exponents of variable(s) are whole numbers and numerical coefficients of various terms are real numbers, is called a polynomial.
In other words,
1. No term of a polynomial has a variable in the denominator;
2. In each term of a polynomial, the exponents of the variable(s) are non-negative integers and
3. Numerical coefficient of each term is a real number.
The terms of a polynomial, having the same variable(s) and the same exponents of the variable(s), are called like terms. A polynomial of degree 2 is called a quadratic polynomial. The degree of a non-zero constant polynomial is taken as zero. When all the coefficients of variable(s) in the terms of a polynomial are zeros, the polynomial is called a zero polynomial. The degree of a zero polynomial is not defined.
Do you know what is a monomial?
An algebraic expression or a polynomial, consisting of only one term, is called a monomial.
Which type of polynomial is called a binomial?
An algebraic expression or a polynomial, consisting of only two terms, is called a binomial.
Which type of algebraic expression is known as trinomial?
An algebraic expression or a polynomial, consisting of only three terms, is called a trinomial.
Tiwari Academy and similar educational websites often provide solutions and study materials to assist students in their preparation. The reasons for using Tiwari Academy platforms for NCERT best solutions includes in simplified format. This platform offers comprehensive solutions that cover all the exercises and examples from the NCERT textbook, making it easier for students to understand and practice.
Many platforms provide step-by-step explanations for solving problems, helping students grasp the concepts more effectively. But they provide best and confined to current syllabus. In addition to solutions, Tiwari Academy platforms often offer additional practice questions and exercises to help students gain confidence and do good practice in their studies.
Online resources like Tiwari Academy are easily accessible, allowing students to study at their own pace and convenience. These platforms may also provide supplementary materials such as video tutorials, quizzes and sample papers to enhance learning. Tiwari Academy and similar platforms may offer study materials and solutions for a wide range of subjects and topics, making them a one-stop destination for students’ academic needs.
10th Maths NCERT Chapter 2 Solutions
Class 10 Exercises solutions are solved in both English as well as Hindi medium in order to help all type of students following latest CBSE Syllabus 2025-26. In prashnavali 2.1 and 2.2 Ganit Solutions, if there is any inconvenient to understand, please inform us, we will short out at our level best.
If you are considering using Tiwari Academy or a similar platform for Class 10 Maths Chapter 2 Polynomials, I recommend visiting their website and exploring the available resources to see and get it as per your learning needs and preferences. You can seek recommendations from teachers or peers to determine the quality and effectiveness of the materials provided by such platforms.
Zeros of Polynomials
The value(s) of the variable for which the value of a polynomial in one variable is zero is (are) called zero(s) of the polynomial. To verify the relationship between the zeroes and coefficients of a given quadratic polynomial, we can find the zeroes of p(x) by factorisation. By taking sum and product of these zeros, we can verify the following results.
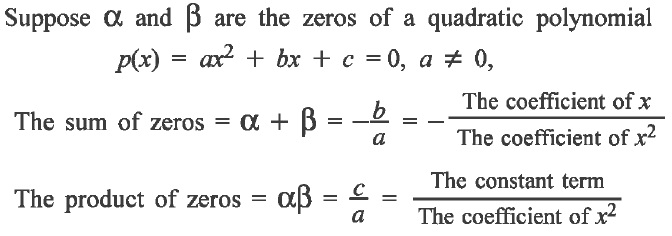
Historical Facts about Polynomials
An elegant way of dividing a polynomial by a liner polynomial was introduced by Paolo Ruffin in 1809. His method is known as Synthetic division, which facilitates the division of a polynomial by a linear polynomial or binomial of the form x – a with the help of the coefficients involved.
Determining the zeros of polynomials, or finding roots of algebraic equations is among the oldest problems in mathematics. The modern way, we use today only developed beginning in the 15th century. Before that, linear equations were written out in words.
What is the History of the mathematical notations?
1. The use of the equal to (=) sign is in Robert Recorde’s book (The Whetstone of Witte in 1557). Plus sign (+) the sign of addition, minus sign (−) the sign of subtraction and the use of an alphabet for an unknown variable in Michael Stifel’s book (Arithemetica integra in 1544).
2. René Descartes, in 1637, introduced the concept of plotting the graph of a polynomial equation. Just because of him, the popularity of use of letters of the alphabet to denote constants and letters from the end of the alphabet (x, y, z, etc.) to denote variables (like 2x, 3y, 7z, etc.) in the general formula for a polynomial in one variable.
How to make good Practice in Class 10 Maths Chapter 2 Polynomials?
Polynomials are said to be one of the important sections of mathematics, especially for Algebra. They’re used in most of the equations and topics of numerical operation in standard 10 and higher also. It wouldn’t be wrong, if we say polynomials are Building Blocks of Maths expressions. Here we will learn about how to solve all exercises of 10th Maths chapter 2. Before learning about the polynomial equation, we have to know its significant importance that makes the topic more interesting. Many Maths process that are done in everyday life can be interpreted as polynomials. With the help of polynomial equations, one can calculate the grocery bill for small and even distance travelled by light in space.
- Step 1: NCERT Solutions for Class 10 Maths Chapter 1 with basic knowledge of Polynomial.
- Step 2: Class 10 Maths chapter 2 solutions with relationship between zeros and coefficient of variables.
- Step 3: NCERT Class 10 Maths Chapter 2 solutions to prove an irrational number as irrational.
- Step 4: Class X Maths Chapter 2 solution help to identify the terminating and non-terminating decimals.
- Step 5: Class 10 Maths Chapter 2 need to build Structural Approach towards Learning.
Step 1: NCERT Solutions for Class 10 Maths Chapter 1 with basic knowledge of Polynomial.

Step 2: Class 10 Maths chapter 2 solutions with relationship between zeros and coefficient of variables.

Step 3: NCERT Class 10 Maths Chapter 2 solutions to prove an irrational number as irrational.

Step 4: Class X Maths Chapter 2 solution help to identify the terminating and non-terminating decimals.

Step 5: Class 10 Maths Chapter 2 need to build Structural Approach towards Learning.

What is the importance of NCERT Solutions for Class 10 Maths Chapter 2 Polynomials?
NCERT Exercises Solutions for Class 10 Maths Chapter 2 Polynomials are essential for students aiming to understand this chapter thoroughly. These solutions offer step-by-step answers to all exercises, including Exercises 2.1, 2.2, 2.3 and 2.4, helping students grasp concepts like zeroes of polynomials, factorization and graphical representation. By practicing these solutions, students gain clarity on solving polynomial equations, which is vital for their exams. Additionally, the NCERT solutions align with the CBSE syllabus, making them reliable resources for exam preparation. They also include important questions, MCQ and practice problems to build confidence and improve problem-solving skills.
What are real life applications of class 10th mathematics chapter 2?
Some real life applications of class 10th mathematics chapter 2 (Polynomials) are:
- Polynomials can be used to model different types of situations, like in the stock market to see how prices will vary with time.
- In physics also polynomials are used to describe the trajectory of projectiles.
- Polynomials used in industries and construction field also.
Polynomials are useful for every person and in every field.
How can students effectively prepare for Class 10 Maths Chapter 2 Polynomials?
To prepare effectively for Class 10 Maths Chapter 2 Polynomials, students should start with the NCERT textbook and solutions, which provide comprehensive coverage of all topics. Using resources like Revision Notes, Video Lectures and Step-by-Step Solutions can help simplify complex problems. Solving Previous Year Questions and attempting Online Tests will improve time management and familiarity with exam patterns. Students can practice with CBSE Sample Papers and focus on key areas highlighted in Important Questions. Regular revision and consistent practice, combined with these resources, ensure a strong grasp of the concepts and excellent performance in exams.
How many exercises are there in chapter 2 of 10th Maths?
There are in all 2 exercises in class 10 mathematics chapter 2 (Polynomials).
In first exercise (Ex 2.1), there is only 1 question having 6 parts.
In second exercise (Ex 2.2), there are 2 questions and each question have 6 parts.
So, there are total 3 questions in class 10 mathematics chapter 2 (Polynomials).
In this chapter there are in all 9 examples. Example 1 is based on Ex 2.1, Examples 2, 3, 4, 5 are based on Ex 2.2.
Where can students find resources for Class 10 Maths Chapter 2 Polynomials?
Students can find reliable resources for Class 10 Maths Chapter 2 Polynomials from various platforms like Tiwari Academy. NCERT solutions are available in textbooks and as Polynomials Solutions PDF for easy access. Numerous educational websites and apps provide downloadable PDFs, Video Lectures and Revision Notes tailored to this chapter. For advanced preparation, students can explore Practice Questions and CBSE Sample Papers curated by experts. Online tests and previous year questions are excellent for practice. These resources ensure comprehensive coverage of the syllabus, providing students with everything needed to master the chapter effectively.
Which questions and examples are important in Class 10 Maths Chapter 2?
In first exercise (Ex 2.1) there is only 1 question with 6 parts and all the part of this question are equally important. In second exercise (Ex 2.2) all questions are important.
Important examples of chapter 2 (Polynomials) class 10th mathematics are example 1, 2, 3, 4, 8, 9.
What should we recall before starting chapter 2 of 10th Maths?
Before starting class 10th mathematics chapter 2 (Polynomials), students should recall chapter 2 (Polynomials) of class 9th mathematics.


