NCERT Exercise Solutions for Class 10 Maths Chapter 6 Triangles in English and Hindi Medium for CBSE Board Exams 2025-26. NCERT Class 10 Mathematics textbook Chapter 6 Solution is prepared as per the CBSE Math books published for new Session. 10th Math Chapter 6 solutions cover all exercises, step-by-step explanations for problems related to similar triangles, Pythagoras theorem and their applications.
Class 10 Maths Exercise 6.1 Solutions
Class 10 Maths Exercise 6.2 Solutions
Class 10 Maths Exercise 6.3 Solutions
Class 10 Maths Chapter 6 Board Questions
Class 10 Maths Chapter 6 Exercises Solutions
Class 10 Maths Exercise 6.1
1. Fill in the blanks using the correct word given in the brackets:
(i) All circles are _____________. (congruent, similar)
See SolutionAll circles are similar. (congruent, similar)
(ii) All squares are _____________. (similar, congruent)
See SolutionAll squares are similar. (similar, congruent)
(iii) All _____________ triangles are similar. (isosceles, equilateral)
See SolutionAll equilateral triangles are similar. (isosceles, equilateral)
(iv) Two polygons of the same number of sides are similar, if (a) their corresponding angles are _____________ and (b) their corresponding sides are _____________. (equal, proportional)
See SolutionTwo polygons of the same number of sides are similar, if (a) their corresponding angles are equal and (b) their corresponding sides are proportional. (equal, proportional)
2. Give two different examples of pair of
(i) similar figures. (ii) non-similar figures.
Answer:
(i) Two equilateral triangles with sides 1 cm and 2 cm.

Two squares with side 1 cm and 2 cm.

(ii) Trapezium and square

Triangle and parallelogram

3. State whether the following quadrilaterals are similar or not:

See SolutionThe sides of quadrilateral PQRS and ABCD are in the same ratio, i.e. 1:2.
The corresponding angles of the two quadrilaterals are not equal.
Hence, the two quadrilaterals are not similar.
Explanation of Class 10 Maths Exercise 6.2
Class 10 Maths Exercise 6.2
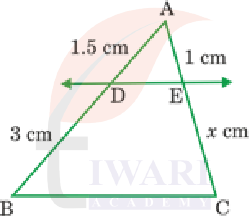
1. In Figure, (i) and (ii), DE || BC. Find EC in (i) and AD in (ii).

See Solution of (i)Let EC = x cm
Given that, DE || BC, therefore
Using Thales theorem, we have
𝐴𝐷/𝐷𝐵 = 𝐴𝐶/𝐸𝐶
⇒ 1.5/3 = 1/𝑥
⇒ 𝑥 = 3 × 1/1.5 = 2
Hence, 𝐸𝐶 = 2.
See Solution of (ii)Let AD = x cm
Given that, DE || BC, therefore
Using Thales theorem, we have
𝐴𝐷/𝐷𝐵 = 𝐴𝐶/𝐸𝐶
⇒ 𝑥/7.2 = 1.8/5.4
⇒ 𝑥 = 1.8 × 7.2/5.4 = 2.4
Hence, 𝐴𝐷 = 2.4.

2. E and F are points on the sides PQ and PR respectively of a Δ PQR. For each of the following cases, state whether EF||QR:
(i) PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2.4 cm
See Solution of (i)Given that, PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm, FR = 2.4 cm, therefore
𝑃𝐸/𝐸𝑄 = 3.9/3 = 1.3 and 𝑃𝐹/𝐹𝑅 = 3.6/2.4 = 1.5
Since, 𝑃𝐸/𝐸𝑄 ≠ 𝑃𝐹/𝐹𝑅,
Hence, EF is not parallel to QR.

(ii) PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm
See Solution of (ii)Given that, PE = 4 cm,
QE = 4.5 cm,
PF = 8 cm,
RF = 9 cm, therefore
𝑃𝐸/𝐸𝑄 = 4/4.5 = 8/9 and 𝑃𝐹/𝐹𝑅 = 8/9
Here, 𝑃𝐸/𝐸𝑄 = 𝑃𝐹/𝐹𝑅,
Hence, according to converse of Thales theorem, EF || QR.

(iii) PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.63 cm
See Solution of (iii)Given that, PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm, PF = 0.36 cm, so
𝑃𝐸/𝐸𝑄 = 0.18/1.28 = 18/128 = 9/64 and 𝑃𝐹/𝐹𝑅 = 0.36/2.56 = 9/64
Here, 𝑃𝐸/𝐸𝑄 = 𝑃𝐹/𝐹𝑅,
Hence, according to converse of Thales theorem, EF || QR.

3. In Figure, if LM || CB and LN || CD, prove that 𝐴𝑀/𝐴𝐵 = 𝐴𝑁/𝐴𝐷.

See SolutionGiven that, in triangle ABC, LM || CB, therefore
According to Thales theorem, we have
𝐴𝑀/𝐴𝐵 = 𝐴𝐿/𝐴𝐶 … (1)
Similarly,
Given that, in triangle ADC, LN || CD, therefore
According to Thales theorem, we have
𝐴𝑁/𝐴𝐷 = 𝐴𝐿/𝐴𝐶 … (2)
From the equation (1) and (2), we have
𝐴𝑀/𝐴𝐵 = 𝐴𝑁/𝐴𝐷
4. In Figure, DE || AC and DF || AE. Prove that 𝐵𝐹/𝐹𝐸 = 𝐵𝐸/𝐸𝐶.

See SolutionGiven that, in ∆ABC, DE || AC, therefore
According to Thales theorem, we have
𝐵𝐷/𝐷𝐴 = 𝐵𝐸/𝐸𝐶 … (1)
Similarly,
In ∆ABC, DF || AE, therefore
According to Thales theorem, we have
𝐵𝐷/𝐷𝐴 = 𝐵𝐹/𝐹𝐸 … (2)
From the equation (1) and (2), we have
𝐵𝐹/𝐹𝐸 = 𝐵𝐸/𝐸𝐶

5. In Figure, DE || OQ and DF || OR. Show that EF || QR.

Solution:
Given that, in ∆POQ, DE || OQ,
Therefore,
According to Thales theorem, we have
𝑃𝐸/𝐸𝑄 = 𝑃𝐷/𝐷𝑂 … (1)
Similarly,
In ∆POR, DF || OR, Therefore,
According to Thales theorem, we have
𝑃𝐹/𝐹𝑅 = 𝑃𝐷/𝐷𝑂 … (2)
From the equation (1) and (2), we have
𝑃𝐸/𝐸𝑄 = 𝑃𝐹/𝐹𝑅

Now,
In triangle PQR,
𝑃𝐸/𝐸𝑄 = 𝑃𝐹/𝐹𝑅 [Proved above]
Therefore,
According to converse of Thales theorem, we have
EF || OR
6. In Figure, A, B and C are points on OP, OQ and OR respectively such that AB||PQ and AC||PR. Show that BC||QR.

Given that, in ∆POQ, AB || PQ,
Therefore,
According to Thales theorem, we have
𝑂𝐴/𝐴𝑃 = 𝑂𝐵/𝐵𝑄 … (1)
Similarly,
In ∆POR, AC || PR,
Therefore,
According to Thales theorem, we have
𝑂𝐴/𝐴𝑃 = 𝑂𝐶/𝐶𝑅 … (2)
From the equation (1) and (2), we have
𝑂𝐵/𝑂𝑄 = 𝑂𝐶/𝐶𝑅

Now, in triangle OQR,
𝑂𝐵/𝑂𝑄 = 𝑂𝐶/𝐶𝑅 [Proved above]
According to converse of Thales theorem, we have
BC || QR.
7. Using Theorem 6.1, prove that a line drawn through the mid-point of one side of a triangle parallel to another side bisects the third side. (Recall that you have proved it in Class IX).

See SolutionLet PQ is a line through the mid-point of AB, parallel to BC intersects AC at Q. i.e., PQ || BC,
In triangle ABC,
According to Thales theorem, we have
𝐴𝑃/𝑃𝐵 = 𝐴𝑄/𝑄𝐶
1 = 𝐴𝑄/𝑄𝐶 [Because AP = PB]
⇒ AQ = QC,
Hence, Q is the mid-point of AC.
8. Using Theorem 6.2, prove that the line joining the mid-points of any two sides of a triangle is parallel to the third side. (Recall that you have done it in Class IX).

See SolutionLet, PQ is a line, which passes through the mid-points of AB and AC. Therefore, AP = PB and AQ = QC.
⇒ 𝐴𝑃/𝑃𝐵 = 1 and 𝐴𝑄/𝑄𝐶 = 1
or
𝐴𝑃/𝑃𝐵 = 𝐴𝑄/𝑄𝐶 = 1
Now, in triangle ABC,
𝐴𝑃/𝑃𝐵 = 𝐴𝑄/𝑄𝐶 [Proved above]
Hence, according to converse of Thales theorem, we have, PQ || BC.
9. ABCD is a trapezium in which AB || DC and its diagonals intersect each other at the point O. Show that 𝐴𝑂/𝐵𝑂 = 𝐶𝑂/𝐷𝑂

See SolutionA line is drawn through the point O, parallel to CD, such that EF||CD.
In ∆ADC, EO || CD
According to Thales theorem, we have,
𝐴𝐸/𝐸𝐷 = 𝐴𝑂/𝑂𝐶 … (1)
Similarly, in ∆ABD, EO || AB
According to Thales theorem, we have,
𝐴𝐸/𝐸𝐷 = 𝐵𝑂/𝑂𝐷 … (2)
From the equation (1) and (2), we get
𝐴𝑂/𝑂𝐶 = 𝐵𝑂/𝑂𝐷
⇒ 𝐴𝑂/𝐵𝑂 = 𝐶𝑂/𝐷𝑂
10. The diagonals of a quadrilateral ABCD intersect each other at the point O such that 𝐴𝑂/𝐵𝑂 = 𝐶𝑂/𝐷𝑂. Show that ABCD is a trapezium.

See SolutionA line is drawn through the point O, parallel to AB, such that EO||AB.
In ∆ABD, EO || AB
According to Thales theorem, we have
𝐴𝐸/𝐸𝐷 = 𝐵𝑂/𝑂𝐷 … (1)
But, given that
𝐴𝑂/𝐵𝑂 = 𝐶𝑂/𝐷𝑂
⇒ 𝐴𝑂/𝐶𝑂 = 𝐵𝑂/𝐷𝑂 … (2)
From the equation (1) and (2), we have
𝐴𝐸/𝐸𝐷 = 𝐴𝑂/𝑂𝐶
⇒ EO || DC [According to converse of Thales theorem, we have]
⇒ AB || OE || DC
⇒ AB || CD
∴ ABCD is a trapezium.
Explanation of Class 10 Maths Exercise 6.3
Class 10 Maths Exercise 6.3
1. State which pairs of triangles in Figure are similar? Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form:

See Solution of (i)∠A = ∠P = 60°, ∠B = ∠Q = 80°, ∠C = ∠R = 40°
Therefore, ∆ABC ∼ ∆PQR [AAA similarity]
See Solution of (ii)𝐴𝐵/𝑄𝑅 = 𝐵𝐶/𝑅𝑃 = 𝐶𝐴/𝑃𝑄,
∴ ∆ABC ∼ ∆QRP [SSS similarity]
See Solution of (iii)Triangles are not similar because the corresponding sides are not proportional.
See Solution of (iv)Triangles are not similar because the corresponding sides are not proportional.
See Solution of (v)Triangles are not similar because the corresponding sides are not proportional.
See Solution of (vi)In ∆DEF,
∠D +∠E +∠F = 180°
⇒ 70° + 80° +∠F = 180
⇒ ∠F = 30°
Similarly, in ∆PQR,
∠P +∠Q +∠R = 180°
⇒ ∠P + 80° +30° = 180° ⇒ ∠P = 70°
In ∆DEF and ∆PQR,
∠D = ∠P [Each 70°]
∠E = ∠Q [Each 80°]
∠F = ∠R [Each 30°]
∴ ∆DEF ∼ ∆PQR [AAA similarity]
2. In Figure, ΔODC ~ ΔOBA, ∠BOC = 125° and ∠CDO = 70°. Find ∠DOC, ∠DCO and ∠OAB.

See SolutionDOB is a straight line.
∴ ∠DOC + ∠COB = 180°
⇒ ∠DOC = 180° − 125° = 55°
∆DOC में, ∠DCO + ∠CDO + ∠DOC = 180°
⇒ ∠DCO + 70° + 55° = 180°
⇒ ∠DCO = 55°
Given that, ∆ODC ∼ ∆OBA.
∴ ∠OAB = ∠ OCD [Corresponding angles of similar triangles]
⇒ ∠OAB = 55°
3. Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O. Using a similarity criterion for two triangles, show that 𝑂𝐴/𝑂𝐶 = 𝑂𝐵/𝑂𝐷.
Solution:

In ∆DOC and ∆BOA,
∠DOC = ∠BOA [Vertically Opposite Angles]
∠CDO = ∠ABO [Alternate Angles]
∠DCO = ∠BAO [Alternate Angles]
∴ ∆DOC ∼ ∆BOA [AAA similarity]
DO/BO = CO/AO
⇒ BO/DO = AO/CO
4. In figure, 𝑄𝑅/𝑄𝑆 = 𝑄𝑇/𝑃𝑅 and ∠1 = ∠2. Show that ∆PQS ∼ ∆TQR.

See SolutionIn ∆PQR, ∠PQR = ∠PRQ
∴ PQ = PR … (1)
Given that,
𝑄𝑅/𝑄𝑆 = 𝑄𝑇/𝑃𝑅
⇒ 𝑄𝑅/𝑄𝑆 = 𝑄𝑇/𝑄𝑃 [From equation (1)] … (2)
In ∆PQS and ∆TQR,
𝑄𝑅/𝑄𝑆 = 𝑄𝑇/𝑄𝑃 [From equation (2)]
∠Q = ∠Q [Common]
∴ ∆PQS ∼ ∆TQR [SAS similarity]
5. S and T are points on sides PR and QR of ΔPQR such that ∠ P = ∠ RTS. Show that ΔRPQ ~ ΔRTS.
Solution:
In ∆RPQ and ∆RST,
∠RTS = ∠QPS [Given]
∠R = ∠R [Common]
∴ ∆RPQ ∼ ∆RTS [AA similarity]

6. In Figure, if Δ ABE ≅ Δ ACD, show that Δ ADE ~ Δ ABC.

See SolutionGiven that, ∆ABE ≅ ∆ACD.
∴ AB = AC [CPCT] … (1)
and, AD = AE [CPCT] … (2)
In ∆ADE and ∆ABC,
𝐴𝐷/𝐴𝐵 = 𝐴𝐸/𝐴𝐶 [From the equation (1) and (2)]
∠A = ∠A [Common]
∴ ∆ADE ∼ ∆ABC [SAS similarity]
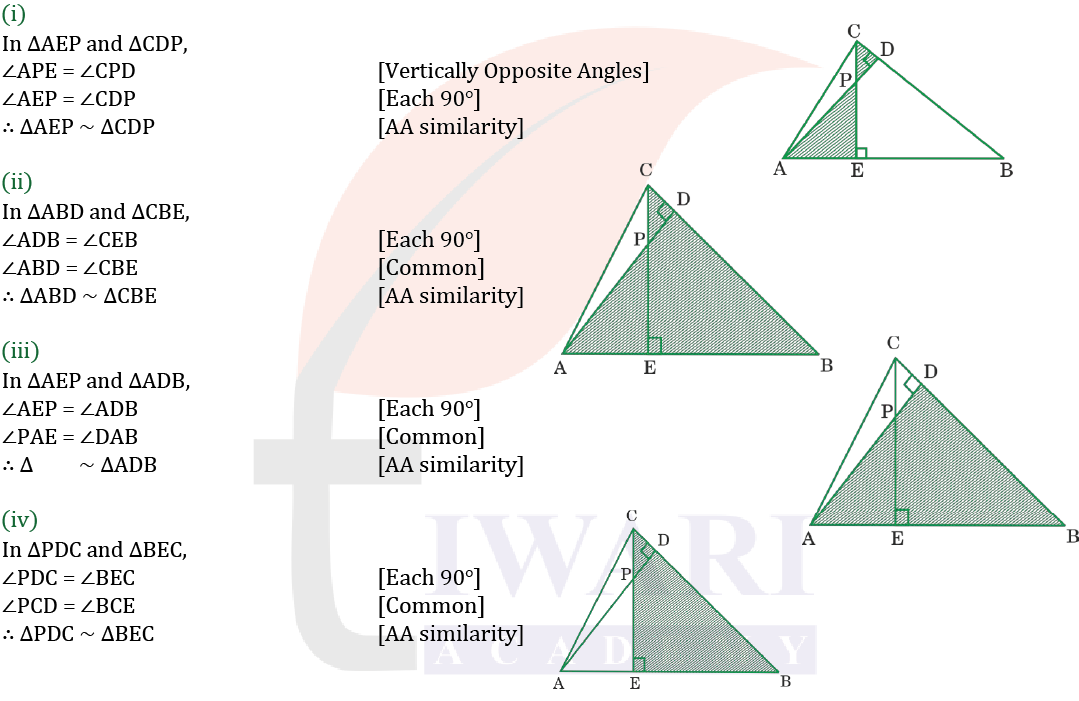
7. In Figure, altitudes AD and CE of Δ ABC intersect each other at the point P. Show that:
(i) ∆AEP ∼ ∆CDP
(ii) ∆ABD ∼ ∆CBE
(iii) ∆AEP ∼ ∆ADB
(iv) ∆PDC ∼ ∆BEC

Solution:
8. E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that ΔABE ~ ΔCFB.
Solution:
In ∆ABE and ∆CFB,
∠A = ∠C [Opposite angles of parallelogram]
∠AEB = ∠CBF [Alternate angles as AE || BC]
∴ ∆ABE ∼ ∆CFB [AA similarity]

9. In Figure, ABC and AMP are two right triangles, right angled at B and M respectively. Prove that:
(i) ∆ABC ∼ ∆AMP
(ii) AB/PQ = AD/PM

See Solution(i) In ∆ABC and ∆AMP,
∠ABC = ∠AMP [Each 90°]
∠A = ∠A [Common]
∴ ∆ABC ∼ ∆AMP [AA similarity]
(ii) ∆ABC ∼ ∆AMP [Proved above]
⇒ AB/PQ = AD/PM [Corresponding parts of similar triangles.]
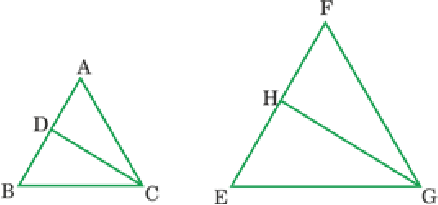
10. CD and GH are respectively the bisectors of ∠ ACB and ∠ EGF such that D and H lie on sides AB and FE of Δ ABC
and Δ EFG respectively. If Δ ABC ~ Δ FEG, show that:
(i) CD/GH = AC/FG
See SolutionGiven that, ∆ABC ∼ ∆FEG
∴ ∠A = ∠F, ∠B = ∠E and ∠ACB = ∠FGE, ∠ACB = ∠FGE
∴ ∠ACD = ∠FGH [CD and GH are the bisectors of equal angles]
and, ∠DCB = HGE [CD and GH are the bisectors of equal angles]
In ∆ACD and ∆FGH,
∠A = ∠F, and ∠ACD = ∠FGH [Proved above]
∴ ∆ACD ∼ ∆FGH [AA similarity]
⇒ CD/GH = AC/FG.
(ii) ∆DCB ∼ ∆HGE
See SolutionIn ∆DCB and ∆HGE,
∠DCB = ∠HGE [Proved above]
∠B = ∠E [Proved above]
∴ ∆DCB ∼ ∆HGE [AA similarity]
(iii) ∆DCA ∼ ∆HGF
See SolutionIn ∆DCA and ∆HGF,
∠ACD = ∠FGH [Proved above]
∠A = ∠F [Proved above]
∴ ∆DCA ∼ ∆HGF [AA similarity]
11. In Figure, E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If AD ⊥ BC and EF ⊥ AC, prove that Δ ABD ~ Δ ECF.

See SolutionGiven that, ABC is an isosceles triangle.
∴ AB = AC ⇒ ∠ABD = ∠ECF
In ∆ABD and ∆ECF,
∠ADB = ∠EFC [Each 90°]
∠ABD = ∠ECF [Proved above]
∴ ∆ABD ∼ ∆ECF [AA similarity]
12. Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of Δ PQR (see Figure). Show that Δ ABC ~ Δ PQR.

See SolutionAD and PM are the median of triangle. Therefore,
BD = BC/2 and QM = QR/2
Given that,
𝐴𝐵/𝑃𝑄 = 𝐵𝐶/𝑄𝑅 = 𝐴𝐷/𝑃𝑀
⇒ 𝐴𝐵/𝑃𝑄 = 1/2 𝐵𝐶/1/2 𝑄𝑅 = 𝐴𝐷/𝑃𝑀
⇒ 𝐴𝐵/𝑃𝑄 = 𝐵𝐷/𝑄𝑀 = 𝐴𝐷/𝑃𝑀
In ∆ABD and ∆PQM,
𝐴𝐵/𝑃𝑄 = 𝐵𝐷/𝑄𝑀 = 𝐴𝐷/𝑃𝑀 [Proved above]
∴ ∆ABD ∼ ∆PQM [SSS similarity]
⇒ ∠ABD = ∠PQM [Corresponding angles of similar triangles]
In ∆ABC and ∆PQR,
∠ABD = ∠PQM [Proved above]
𝐴𝐵/𝑃𝑄 = 𝐵𝐶/𝑄𝑅
∴ ∆ABC ∼ ∆PQR [SAS similarity]
13. D is a point on the side BC of a triangle ABC such that ∠ ADC = ∠ BAC. Show that CA² = CB.CD.

See SolutionIn ∆ADC and ∆BAC,
∠ADC = ∠BAC [Given]
∠ACD = ∠BCA [Common]
∴ ∆ADC ∼ ∆BAC [AA similarity]
We know that the corresponding sides of similar triangles are proportional.
Therefore
CA/CB = CD/CA
⇒ CA² = CB × CD.
14. Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and
median PM of another triangle PQR. Show that Δ ABC ~ Δ PQR.
Solution:
Given that, 𝐴𝐵/𝑃𝑄 = 𝐴𝐶/𝑃𝑅 = 𝐴𝐷/𝑃𝑀

Produce AD and PM to E and L such that AD = DE and PM = DE.
Now join B to E, C to E, Q to L and R to L.
AD and PM are medians of triangle, therefore
BD = DC and QM = MR
and, AD = DE [By construction]
and, PM = ML [By construction]
So, the diagonals of ABEC bisecting each other at D, therefore ABEC is a parallelogram.

Similarly, PQLR is also a parallelogram. ∴ AC = BE, AB = EC and PR = QL, PQ = LR
Given that, 𝐴𝐵/𝑃𝑄 = 𝐴𝐶/𝑃𝑅 = 𝐴𝐷/𝑃𝑀
⇒ 𝐴𝐵/𝑃𝑄 = 𝐵𝐸/𝑄𝐿 = 2𝐴𝐷/2𝑃𝑀
⇒ 𝐴𝐵/𝑃𝑄 = 𝐵𝐸/𝑄𝐿 = 𝐴𝐸/𝑃𝐿
∴ ∆ABE ∼ ∆PQL [SSS similarity]
We know that the corresponding angles of similar triangles are equal. Therefore
∴ ∠BAE = ∠QPL … (1)
Similarly, ∆AEC ∼ ∆PLR and
∠CAE = ∠RPL … (2)
Adding the equations (1) and (2), we get
∠BAE + ∠CAE = ∠QPL + ∠RPL
⇒ ∠CAB = ∠RPQ … (3)
In ∆ABC and ∆PQR,
𝐴𝐵/𝑃𝑄 = 𝐴𝐶/𝑃𝑅 [Given]
∠CAB = ∠RPQ [From the equation (3)]
∴ ∆ABC ∼ ∆PQR [SAS similarity]
15. A vertical pole of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.

See SolutionLet CD be the pole and AB is tower.
Therefore, DF and BE are the shadows of pole and tower.
In ∆ABE and ∆CDF,
∠DCF = ∠BAE [Angle of sun at same place]
∠CDF = ∠ABE [Each 90°]
∴ ∆ABE ∼ ∆CDF [AA similarity]
𝐴𝐵/𝐶𝐷 = 𝐵𝐸/𝑄𝐿 ⇒ 𝐴𝐵/6 = 28/4 ⇒ 𝐴𝐵 = 42 𝑚
Hence, the height of the tower is 42 m.
16. If AD and PM are medians of triangles ABC and PQR, respectively where Δ ABC ~ Δ PQR, prove that 𝐴𝐵/𝑃𝑄 = 𝐴𝐷/𝑃𝑀.
See SolutionGiven that: ∆ABC ∼ ∆PQR
We know that the corresponding sides of similar triangles are proportional. Therefore
𝐴𝐵/𝑃𝑄 = 𝐴𝐶/𝑃𝑅 = 𝐵𝐶/𝑄𝑅 … (1)
and, ∠A = ∠P, ∠B = ∠Q, ∠C = ∠R … (2)
AD and PM are medians of triangle. Therefore
BD = BC/2 and QM = QR/2 … (3)
From the equation (1) and (3), we have
𝐴𝐵/𝑃𝑄 = 𝐵𝐷/𝑄𝑀 … (4)
In ∆ABD and ∆PQM,
∠B = ∠Q [From the equation (2)]
𝐴𝐵/𝑃𝑄 = 𝐵𝐷/𝑄𝑀 [From the equation (4)]
∴ ∆ABD ∼ ∆PQM [SAS similarity]
𝐴𝐵/𝑃𝑄 = 𝐵𝐷/𝑄𝑀 = 𝐴𝐷/𝑃𝑀

10th Maths Chapter 6 Exercise 6.1 Solutions
10th Maths Chapter 6 Exercise 6.2 Solutions
10th Maths Chapter 6 Exercise 6.3 Solutions
Class 10th Maths Chapter 6 Solutioins for State Boards
- Class 10 Maths Chapter 6 Exercise 6.1
- Class 10 Maths Chapter 6 Exercise 6.2
- Class 10 Maths Chapter 6 Exercise 6.3
- Class 10 Maths Chapter 6 Exercise 6.4
- Class 10 Maths Chapter 6 Exercise 6.5
- Class 10 Maths Chapter 6 Exercise 6.6
- Class 10th Maths Chapter 6 NCERT Book
- Class 10 Maths NCERT Solutions
- Class 10 all Subjects NCERT Solutions
Students often rely on NCERT Book Solutions for Class 10 Mathematics Triangles for a detailed explanation of complex problems. The Class 10 NCERT Math Chapter 6 Exercise Solutions focus on the properties and criteria for similarity of triangles, which are crucial for understanding geometry in higher classes. The NCERT Class 10th Maths Triangles Solutions PDF is widely used for its portability and ease of use, allowing students to prepare for their exams anytime.
With free downloadable resources like CBSE Class 10 Maths Chapter 6 NCERT Exercise Solutions PDF, students can easily find answers and strengthen their problem-solving skills. Teachers and tutors also recommend Triangles Chapter 6 Class 10 Solutions for building a strong foundation in geometry. By practicing these Class 10 NCERT Book Chapter 6 Maths Solutions, students can improve their performance and approach mathematical problems with confidence.
Key Points to Focus on in Class 10 Maths Chapter 6: Triangles for Board Exams
Class 10 Maths Chapter 6, Triangles, focuses on similarity criteria (AAA, SSS, SAS), Pythagoras theorem and its converse, properties of similar triangles and their applications in proving geometric results. Understanding proportionality theorems, solving exercise problems and practicing proofs are crucial for board exams, as these topics carry significant weightage.
| Day | Topics to Cover | Practice Exercises |
|---|---|---|
| Day 1 | Introduction to Similarity of Triangles | NCERT Exercise 6.1 |
| Day 2 | Criteria for Similarity (AAA, SSS, SAS) | NCERT Exercise 6.2 |
| Day 3 | Applications of Similar Triangles | NCERT Exercise 6.3 |
| Day 4 | Pythagoras Theorem | Extra Questions of Exercise 6.2 |
| Day 5 | Converse of Pythagoras Theorem | Extra Questions of Exercise 6.3 |
| Day 6 | Miscellaneous Problems and Revision | NCERT Miscellaneous Exercise |
| Class: 10 | Mathematics |
| Chapter 6: | Triangles |
| Content: | NCERT Exercises Solutions |
| Content Format: | Online Text, Images, PDF and Videos |
| Academic Session: | Year 2025-26 Board Exams |
| Medium: | English and Hindi Medium |
History of similar triangles
A Greek mathematician Thales gave an important relation relating to two equiangular triangles that ‘The ratio of any two corresponding sides in two similar triangles is always the same. If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio’. Which is known as the Basic Proportionality Theorem or the Thales Theorem.
There are so many other important theorems based on similar triangles like If in two triangles, sides of one triangle are proportional to (i.e., in the same ratio of ) the sides of the other triangle, then their corresponding angles are equal and hence the two triangles are similar. Or if two angles of one triangle are respectively equal to two angles of another triangle, then the two triangles are similar. Download CBSE board Exams papers, for the questions based on BPT in board exams.
Historical Facts! – Similar Triangles
1. We know that Pythagoras theorem is popular. It has wide range of applications. In ancient Indian Maths society done well. Bodhayan (800 BC) wrote ‘Sulb Sutras’. It depicts Pythagoras theorem. Bhashkaracharya and Brahmaputra gave different proofs of it.
2. We all know that Leonardo De Vinchi was the great artist. He was an architect. He was famous for his painting ‘Mona Lisa’. He gave a beautiful proof for this theorem.
3. Thales of Miletus (624 – 546 BC, Greece) was the first known philosopher with math knowledge. He worked as the first use of deductive reasoning in geometry. He discovered many propositions in geometry. He is believed to have found the heights of the pyramids in Egypt. He used the shadows and principle of similar triangles. We could get the Height of pyramids using facts of trigo.
4. Brahma Gupta’s theorem (628 A.D.):
The rectangle contained by any two sides of a triangle, is equal to rectangle contained by altitude drawn to the third side and the circum diameter.
5. Galileo Galilei explained about the universe. He told no one can read it until we have learnt its language. Its language includes the letters like triangles, circles and other Maths figures. Without learning, it is impossible to comprehend a single word.
Why are NCERT Textbook Solutions for Class 10 Maths Chapter 6 Triangles important?
NCERT Exercise Solutions for Class 10 Mathematics Chapter 6 Triangles provide detailed explanations and step-by-step methods to solve problems related to the topic of triangles. This chapter is crucial for understanding key concepts like the criteria for similarity of triangles, the Pythagoras theorem and their applications. These solutions are designed according to the CBSE syllabus, ensuring students can prepare thoroughly for board exams. By practicing these solutions, students can improve their conceptual clarity, enhance their problem-solving skills, and gain confidence in tackling questions of varying difficulty levels.
What is meant by Similarity or Similar Triangle in 10th Maths Chapter6?
According to 10th Maths chapter 6, similarity of geometric figures is an important concept of Euclidean geometry. Similarity in a geometric transformation of one figure into the other figure such that the measure of all linear elements of one figure are in proportion to the corresponding linear elements of the other figure. Two triangles (or any polygons of the same number of sides) are similar, if (i) their corresponding angles are equal and (ii) their corresponding sides are in the same ratio (or proportion). All congruent figures are similar but the similar figures need not be congruent.
Where can I find a PDF of Class 10 Maths Chapter 6 Solutions?
You can easily find a PDF of Class 10 Maths Chapter 6 Solutions online through various educational platforms and websites offering free or downloadable resources. These PDFs provide the complete set of solutions for exercises from the Triangles chapter, ensuring that students can practice offline anytime. This convenience makes it an excellent resource for last-minute revisions or when studying without internet access. The downloadable PDFs often include step-by-step explanations, solved examples and tips for tackling tricky questions, making them a valuable aid for students preparing for board exams.
In class 10th mathematics, How many exercises, questions and examples are there in chapter 6 Triangles?
There are in all 3 exercises in class 10 mathematics chapter 6 (Triangles).
In first exercise (Ex 6.1), there are only 3 questions.
In second exercise (Ex 6.2), there are in all 10 questions.
In third exercise (Ex 6.3), there are in all 16 questions.
So, there are total 23 questions in class 10 mathematics chapter 6 (Triangles).
In this chapter there are in all 14 examples. Examples 1, 2, 3 are based on Ex 6.2, Examples 4, 5, 6, 7, 8 are based on Ex 6.3.
How can NCERT Solutions for Class 10 Maths Triangles help in board exam preparation?
NCERT Solutions for Class 10 Mathematics Triangles are specifically designed to align with the CBSE board exam pattern. They cover all exercises in detail, explaining concepts like the similarity of triangles, proportionality theorems and Pythagoras theorem in a simplified manner. By practicing these solutions, students can develop a clear understanding of key topics and improve their accuracy in solving questions. The solutions provide insights into how to structure answers for better scoring in exams. Regular practice with these resources ensures that students are well-prepared and confident when appearing for their board exams.
Is there any chapter of class 9th maths which students should revise before starting class 10th maths chapter 6 (Triangles)?
Yes, before starting class 10th mathematics chapter 6 (Triangles), students should revise chapter 7 (Triangles) of class 9th mathematics.
Are the NCERT Class 10 Maths Chapter 6 Solutions available for free?
Yes, NCERT Class 10 Mathematics Chapter 6 Solutions are widely available for free on various educational websites like Tiwari Academy. Many platforms offer these solutions as downloadable PDFs, allowing students to access them offline for convenient learning. Free resources are particularly helpful for students who need reliable, step-by-step guidance without incurring additional costs. These solutions are comprehensive, covering all exercises in the Triangles chapter and adhering to the CBSE curriculum. Free access ensures that every student, regardless of their background, can prepare effectively and excel in their mathematics board exams.
How many theorems are there in class 10th Maths chapter 6 Triangles?
There are 9 theorems in chapter 6 (Triangles) of class 10th Maths. Theorem 6.1 is known as Basic Proportionality Theorem, Theorem 6.2 is converse of Basic Proportionality Theorem, Theorems 6.3, gives similarity criterion for two triangles.
Which theorem of 10th Maths chapter 6 Triangles is asked for Proof in Exams?
From chapter 6 (Triangles) of class 10 Maths, Proof of Theorem 6.1 (Basic Proportionality Theorem), Theorem 6.3 (area theorem), can come in exam or you can say that these theorems are important.
Which is the easiest exercise of chapter 6 (Triangles) of class 10 math?
Exercise 6.1 is the easiest exercise of chapter 6 (Triangles) of class 10 math.


