NCERT Textbook Solutions for Class 10 Maths Chapter 7 Coordinate Geometry Exercises in Hindi and English Medium revised for CBSE Session 2025-26. NCERT Class 10 Mathematics Book Chapter 7 solution is simplified as per the NCERT Math textbooks published for CBSE 2025-26 Exams.
Select Your Topic
► Class 10 Maths Exercise 7.1
► Class 10 Maths Exercise 7.2
Study Material for Board Exams
• Questions from Board Papers
• Class 10 Maths Chapter 7 MCQs
For Session 2025-26 Class 10 Maths Chapter 7 Solutions
Class 10 Maths Exercise 7.1
1. Find the distance between the following pairs of points:
(i) (2, 3), (4, 1)
See SolutionUsing the distance formula:
√[(𝑥₂ − 𝑥₁)² + (𝑦₂ − 𝑦₁)²]
Distance between 𝐴(2, 3) and 𝐵(4, 1) is given by 𝐴𝐵
= √{(4 − 2)² + (1 − 3)²}
= √(4 + 4)
= √8
= 2√2.
(ii) (−5, 7), (−1, 3) (iii) (𝑎, 𝑏), (−𝑎, −𝑏)
See SolutionUsing the distance formula:
√[(𝑥₂ − 𝑥₁)² + (𝑦₂ − 𝑦₁)²]
Distance between 𝑃(−5, 7) and 𝑄(−1, 3) is given by 𝑃𝑄
= √{[−1 − (−5)]² + (3 − 7)²}
= √(16 + 16)
= √32
= 4√2.
(iii) (𝑎, 𝑏), (−𝑎, −𝑏)
See SolutionUsing the distance formula:
√[(𝑥₂ − 𝑥₁)² + (𝑦₂ − 𝑦₁)²]
Distance between 𝑀(𝑎, 𝑏) and 𝑁(−𝑎, −𝑏) is given by 𝑀𝑁
= √{[−𝑎 − (−𝑎)]² + [−𝑏 − (−𝑏)]²}
= √(4𝑎² + 4𝑏²)
= 2√(𝑎² + 𝑏²).
2. Find the distance between the points (0, 0) and (36, 15). Can you now find the distance between the two towns A and B discussed in Section 7.2.
See SolutionHere, 𝑃(0, 0) and 𝑄(36, 15), using distance formula:
√[(𝑥₂ − 𝑥₁)² + (𝑦₂ − 𝑦₁)²]
Distance between 𝑃(0, 0) and 𝑄(36, 15) is given by 𝑃𝑄
= √[(36 − 0)² + (15 − 0)²]
= √(1296 + 225)
= √1521
= 39
Using the distance formula: √(𝑥₂ − 𝑥₁)² + (𝑦₂ − 𝑦₁)², we can find the distance between the two towns.
3. Determine if the points (1, 5), (2, 3) and (– 2, – 11) are collinear.
See SolutionHere, 𝐴(1, 5), B(2, 3) and 𝐶(−2, −11).
Using distance formula:
√[(𝑥₂ − 𝑥₁)² + (𝑦₂ − 𝑦₁)²]
𝐴𝐵 = √{(2 − 1)² + (3 − 5)²}
= √(1 + 4)
= √5
𝐵𝐶 = √{(−2 − 2)² + (−11 − 3)²}
= √(16 + 196)
= √212
𝐶𝐴 = √{[1 − (−2)]² + [5 − (−11)]²}
= √(9 + 256)
= √265
Here, 𝐴𝐵 + 𝐵𝐶 = √5 + √212 ≠ √265 = 𝐴𝐶
Hence, the points 𝐴(1, 5), B(2, 3) and 𝐶(−2, −11) are not collinear.
4. Check whether (5, – 2), (6, 4) and (7, – 2) are the vertices of an isosceles triangle.
See SolutionGiven points: 𝐴(5, −2), B(6, 4) and 𝐶(7, −2) are vertices of triangle.
Using distance formula:
√[(𝑥₂ − 𝑥₁)² + (𝑦₂ − 𝑦₁)²]
𝐴𝐵 = √{(6 − 5)² + [4 − (−2)]²} = √(1 + 36) = √37
𝐵𝐶 = √{(7 − 6)² + (−2 − 4)²} = √(1 + 36) = √37
𝐶𝐴 = √{(5 − 7)² + [−2 − (−2)]²} = √(4 + 0) = 2
Here, 𝐴𝐵 = 𝐵𝐶 ≠ 𝐴𝐶
Hence, the points (5, – 2), (6, 4) and (7, – 2) are the vertices of an isosceles triangle.
5. In a classroom, 4 friends are seated at the points A, B, C and D as shown in Figure. Champa and Chameli walk into the class and after observing for a few minutes Champa asks Chameli, “Don’t you think ABCD is a square?” Chameli disagrees. Using distance formula, find which of them is correct.
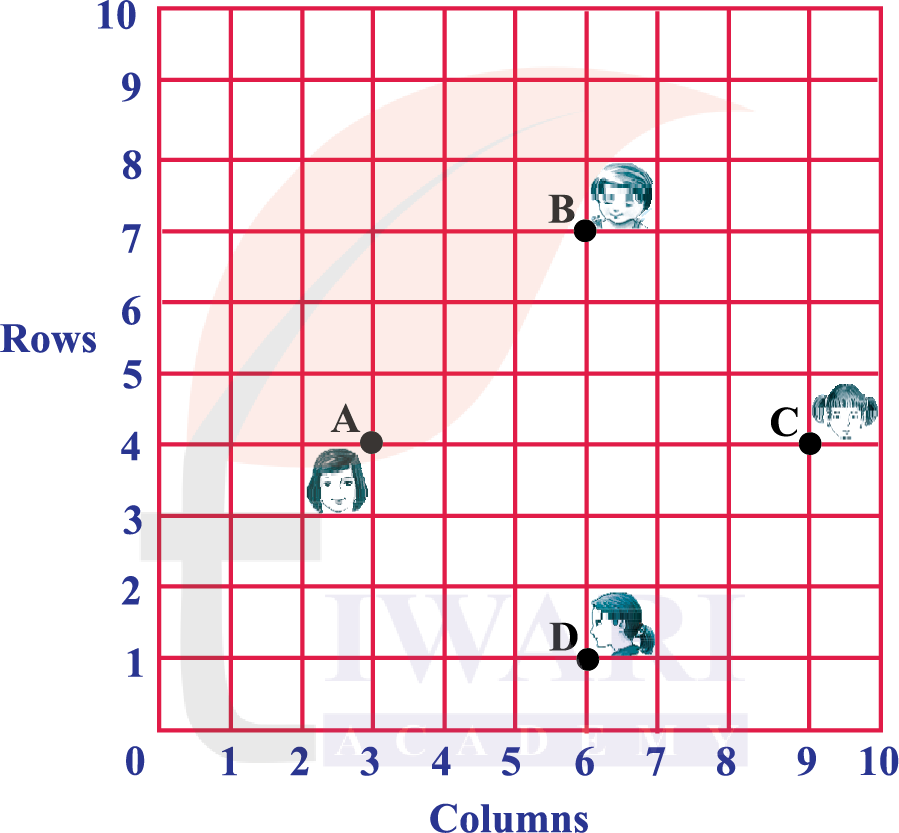
See SolutionFrom the figure, the coordinates of points A, B, C and D are
𝐴(3, 4), B(6, 7), C(9, 4) and D(6, 1).
𝐴𝐵 = √{(6 − 3)² + (7 − 4)²} = √(9 + 9) = √18 = 3√2
𝐵𝐶 = √{(9 − 6)² + (4 − 7)²} = √(9 + 9) = √18 = 3√2
𝐶𝐷 = √{(6 − 9)² + (1 − 4)²} = √(9 + 9) = √18 = 3√2
𝐷𝐴 = √{(3 − 6)² + (4 − 1)²} = √(9 + 9) = √18 = 3√2
All the sides of quadrilateral are equal, so it may be a square or rhombus on the basis of its diagonal.
𝐴𝐶 = √{(9 − 3)² + (4 − 4)²} = √(36 + 0) = 6
𝐵𝐷 = √{(6 − 6)² + (1 − 7)²} = √(0 + 36) = 6
Here, 𝐴𝐵 = 𝐵𝐶 = 𝐶𝐷 = 𝐷𝐴 and 𝐴𝐶 = 𝐵𝐷
Hence, ABCD is a square. So, Champa is correct.
6. Name the type of quadrilateral formed, if any, by the following points, and give reasons for your answer:
(i) (−1, −2), (1, 0), (−1, 2), (−3, 0)
See Solution𝐴𝐵 = √{[1 − (−1)]² + [0 − (−2)]²} = √(4 + 4) = √8 = 2√2
𝐵𝐶 = √{(−1 − 1)² + (2 − 0)²} = √(4 + 4) = √8 = 2√2
𝐶𝐷 = √{[−3 − (−1)]² + (0 − 2)²} = √(4 + 4) = √8 = 2√2
𝐷𝐴 = √{[−1 − (−3)]² + (−2 − 0)²} = √(4 + 4) = √8 = 2√2
All the sides of quadrilateral are equal, so it may be a square or rhombus on the basis of its diagonal.
𝐴𝐶 = √{[1 − (−1)]² + [2 − (−2)]²} = √(0 + 16) = 4
𝐵𝐷 = √{(−3 − 1)² + (0 − 0)²} = √(16 + 0) = 4
Here, 𝐴𝐵 = 𝐵𝐶 = 𝐶𝐷 = 𝐷𝐴 and 𝐴𝐶 = 𝐵𝐷
Hence, ABCD is a square.
(ii) (−3, 5), (3, 1), (0, 3), (−1, −4)
See Solution𝐴𝐵 = √{[3 − (−3)]² + (1 − 5)²} = √(36 + 16) = √52 = 2√13
𝐵𝐶 = √{(0 − 3)² + (3 − 1)²} = √(9 + 4) = √13
𝐶𝐷 = √{(1 − 0)² + (−4 − 3)²} = √(1 + 49) = √50 = 5√2
𝐷𝐴 = √{[−3 − (−1)]² + [5 − (−4)]²} = √(4 + 81) = √85
𝐴𝐶 = √{[0 − (−3)]² + (3 − 5)²} = √(9 + 4) = √13
𝐵𝐷 = √{(−1 − 3)² + (−4 − 1)²} = √(16 + 25) = √41
Here, 𝐴𝐶 + 𝐵𝐶 = 𝐴𝐵, it means the point 𝐶 lies on side 𝐴𝐵 or A, B, C are collinear.
Hence, the quadrilateral ABCD is not possible.
(iii) (4, 5), (7, 6), (4, 3), (1, 2)
See Solution𝐴𝐵 = √{(7 − 4)² + (6 − 5)²} = √(9 + 1) = √10
𝐵𝐶 = √{(4 − 7)² + (3 − 6)²} = √(9 + 9) = √18
𝐶𝐷 = √{(1 − 4)² + (2 − 3)²} = √(9 + 1) = √10
𝐷𝐴 = √{(4 − 1)² + (5 − 2)²} = √(9 + 9) = √18
The opposite sides of quadrilateral are equal. It may be a parallelogram or rectangle. It can be justified with the help of lengths of its diagonal.
𝐴𝐶 = √{(4 − 4)² + (3 − 5)²} = √(0 + 4) = 2
𝐵𝐷 = √{(1 − 7)² + (2 − 6)²} = √(36 + 16) = √52 = 2√13
Here, 𝐴𝐵 = 𝐶𝐷, 𝐵𝐶 = 𝐴𝐷 and 𝐴𝐶 ≠ 𝐵𝐷.
Hence, ABCD is a parallelogram.
7. Find the point on the x-axis which is equidistant from (2, –5) and (–2, 9).
See SolutionLet 𝑃(𝑥, 0) be any point on 𝑥−axis, which is equidistant from 𝐴(2, −5) and 𝐵(−2, 9).
Therefore, 𝑃𝐴 = 𝑃𝐵
⇒ √{(2 − 𝑥)² + (−5 − 0)²} = √{(−2 − 𝑥)² + (9 − 0)²}
⇒ √(4 + 𝑥² − 4𝑥 + 25) = √(4 + 𝑥² + 4𝑥 + 81)
Squaring both the sides
4 + 𝑥² − 4𝑥 + 25 = 4 + 𝑥² + 4𝑥 + 81
⇒ −8𝑥 = 81 − 25 = 56
⇒ 𝑥 = −56/8 = −7
Hence, 𝑃(−7, 0) is the point on the x-axis which is equidistant from (2, –5) and (–2, 9).
8. Find the values of y for which the distance between the points P(2, – 3) and Q(10, y) is 10 units.
See SolutionThe distance between 𝑃(2, −3) and 𝑄(10, 𝑦) is 10 units.
⇒ √{(10 − 2)² + [𝑦 − (−3)]²} = 10
⇒ √(64 + 𝑦² + 9 + 6𝑦) = 10
Squaring both sides
64 + 𝑦² + 9 + 6y = 100
⇒ 𝑦² + 6𝑦 − 27 = 0
⇒ 𝑦² + 9𝑦 − 3𝑦 − 27 = 0
⇒ 𝑦(𝑦 + 9) − 3(𝑦 + 9) = 0
⇒ (𝑦 + 9)(𝑦 − 3) = 0
⇒ (𝑦 + 9) = 0 or (𝑦 − 3) = 0
⇒ 𝑦 = −9 or 𝑦 = 3
9. If Q(0, 1) is equidistant from P(5, –3) and R(x, 6), find the values of x. Also find the distances QR and PR.
See Solution𝑄(0, 1) is equidistant from the points 𝑃(5, −3) and 𝑅(𝑥, 6).
Therefore, 𝑄𝑃 = 𝑄𝑅
⇒ √{(5 − 0)² + (−3 − 1)²} = √{(𝑥 − 0)² + (6 − 1)²}
⇒ √(25 + 16) = √(𝑥² + 25)
Squaring both the sides
25 + 16 = 𝑥² + 25
⇒ 𝑥² = 16
⇒ 𝑥 = ±4
If 𝑥 = 4,
𝑄𝑅 = √{(4 − 0)² + (6 − 1)²} = √(16 + 25) = √41
𝑃𝑅 = √{(4 − 5)² + [6 − (−3)]²} = √(1 + 81) = √82
If 𝑥 = −4,
𝑄𝑅 = √{(−4 − 0)² + (6 − 1)²} = √(16 + 25) = √41
𝑃𝑅 = √{(−4 − 5)² + [6 − (−3)]²} = √(81 + 81) = √162 = 9√2.
10. Find a relation between x and y such that the point (x, y) is equidistant from the point (3, 6) and (– 3, 4).
See SolutionPoint 𝑃(𝑥, 𝑦) is equidistant from 𝐴(3, 6) and 𝐵(−3, 4). Therefore, 𝑃𝐴 = 𝑃𝐵
⇒ √{(3 − 𝑥)² + (6 − y)²} = √{(−3 − 𝑥)² + (4 − y)²}
⇒ √(9 + 𝑥² − 6𝑥 + 36 + 𝑦² − 12𝑦) = √(9 + 𝑥² + 6𝑥 + 16 + 𝑦² − 8𝑦)
Squaring both sides
9 + 𝑥² − 6𝑥 + 36 + 𝑦² − 12𝑦 = 9 + 𝑥² + 6𝑥 + 16 + 𝑦² − 8𝑦
⇒ −12𝑥 − 4𝑦 = −20
⇒ 3𝑥 + 𝑦 = 5.
Class 10 Maths Exercise 7.2
1. Find the coordinates of the point which divides the join of (–1, 7) and (4, –3) in the ratio 2:3.
See SolutionLet the point 𝑃 divides the line joining the points 𝐴(−1, 7) and 𝐵(4, −3) into 2 ∶ 3.
𝐴(−1, 7) 2 𝑃 3 𝐵(4, −3)
Using section formula (𝑚₁𝑥₂ + 𝑚₂𝑥₁)/( 𝑚₁ + 𝑚₂) ,(𝑚₁𝑦₂ + 𝑚₂𝑦₁)/(𝑚₁ + 𝑚₂) , the coordinates of 𝑃 are given by
[(2 × 4 + 3 × (−1)]/(2 + 3) , [2 × (−3) + 3 × 7]/(2 + 3)
= (5/5 , 15/5)
= (1, 3).

2. Find the coordinates of the points of trisection of the line segment joining (4, –1) and (–2, –3).
See SolutionLet the points 𝑃 and 𝑄 be the points of trisection of the line joining 𝐴(4, −1) and 𝐵(−2, −3).
Hence, 𝐴𝑃: 𝑃𝐵 = 1: 2
Using section formula: ((𝑚₁𝑥₂ + 𝑚₂𝑥₁)/(𝑚₁ + 𝑚₂) , (𝑚₁𝑦₂ + 𝑚₂𝑦₁)/(𝑚₁ + 𝑚₂))
The coordinates of 𝑃 are given by
({1 × (−2) + 2 × 4}/{1 + 2}, {1 × (−3) + 2 × (−1)}/{1 + 2})
= (6/3, −5/3)
= ( 2, − 5 /3 ) and 𝐴𝑄: 𝑄𝐵 = 2: 1
Using section formula ({𝑚₁𝑥₂ + 𝑚₂𝑥₁}/{𝑚₁ + 𝑚₂} ,{𝑚₁𝑦₂ + 𝑚₂𝑦₁}/{𝑚₁ + 𝑚₂}) , the coordinates of 𝑄 are given by
( {2 × (−2) + 1 × 4}/{2 + 1}, {2 × (−3) + 1 × (−1)}/{2 + 1})
= (0/3, −7/3 ) = (0, −7/3).

3. To conduct Sports Day activities, in your rectangular shaped school ground ABCD, lines have been drawn with chalk powder at a distance of 1m each. 100 flower pots have been placed at a distance of 1m from each other along AD, as shown in Figure. Niharika runs ¹⁄₄th the distance AD on the 2nd line and posts a green flag. Preet runs ¹⁄₅th the distance AD on the eighth line and posts a red flag. What is the distance between both the flags? If Rashmi has to post a blue flag exactly halfway between the line segment joining the two flags, where should she post her flag?

See SolutionNiharika runs ¹⁄₄th the distance AD on the 2nd line and posts a green flag.
Therefore, the coordinates of the flag posted by Niharika = 𝑁(2, ¹⁄₄ × 100) = 𝑁(2, 25)
Preet runs ¹⁄₅th the distance AD on the eighth line and posts a red flag.
Therefore, the coordinates of flag posted by Preet = 𝑃(8, ¹⁄₅ × 100) = 𝑃(8, 20)
Distance between the two flags = 𝑁𝑃 = √{(8 − 2)² + (20 − 25)²} = √{36 + 25} = √61
If Rashmi has to post a blue flag exactly halfway between the line segment joining the two flags, then the coordinates of the flag posted by Rashmi = coordinates of mid points of 𝑁𝑃
= 𝑅({ 𝑥₁ + 𝑥₂}/ 2, {𝑦₁ + 𝑦₂}/2)
= 𝑅({2 + 8}/2, {25 + 20}/2)
= 𝑅(5, 45/2)
= 𝑅(5, 22.5)
Hence, Rashmi should post her flag in fifth line at a distance of 22.5 𝑚.
4. Find the ratio in which the line segment joining the points (– 3, 10) and (6, – 8) is divided by (– 1, 6).
See SolutionLet the point 𝑃(−1, 6), divides the line segment joining 𝐴(−3, 10) and 𝐵(6, −8) into 𝑘: 1.
Using the section formula ({𝑘.𝑥₂ + 1.𝑥₁}/{𝑘+1}, {k.𝑦₂ + 1.𝑦₁}/{𝑘+1}), the coordinates of point 𝑃
𝑃(−1, 6) = ({𝑘 × 6 + 1 × (−3)}/{𝑘 + 1}, {𝑘 × (−8) + 1 × 10}/{𝑘 + 1})
⇒ 𝑃(−1, 6) = ({6𝑘 − 3}/{𝑘 + 1}, {−8𝑘 + 10}/{𝑘 + 1})
On comparing
{6𝑘 − 3}/{𝑘 + 1} = −1 and {−8𝑘 + 10}/{𝑘 + 1} = 6
⇒ 6𝑘 − 3 = −𝑘 − 1
⇒ 7𝑘 = 2
⇒ 𝑘 = 2/7
Hence, the point 𝑃(−1, 6), divides the line segment joining the points 𝐴(−3, 10) and 𝐵(6, −8) into 2: 7.

5. Find the ratio in which the line segment joining A(1, – 5) and B(– 4, 5) is divided by the x-axis. Also find the
coordinates of the point of division.
See SolutionLet the line segment joining the points 𝐴(1, −5) and 𝐵(−4, 5) is divided by 𝑥−axis at point 𝑃(𝑥, 0) into 𝑘: 1.
Using the section formula ({𝑘.𝑥₂+1.𝑥₁}/{𝑘+1}, {k.𝑦₂+1.𝑦₁}/{𝑘+1}), the coordinates of point 𝑃
𝑃(𝑥, 0) = ({𝑘 × (−4) + 1 × 1}/{𝑘 + 1}, {𝑘 × 5 + 1 × (−5)}/{𝑘 + 1})
⇒ 𝑃(𝑥, 0) = ({−4𝑘 + 1}/{𝑘 + 1}, {5𝑘 − 5}/{𝑘 + 1})
On comparing
{−4𝑘 + 1}/{𝑘 + 1} = 𝑥 and {5𝑘 − 5}/{𝑘 + 1} = 0
⇒ 5𝑘 − 5 = 0
⇒ 𝑘 = 1
Putting the value of 𝑘 in {−4𝑘+1}/{𝑘+1} = 𝑥, we have
{−4(1) + 1}/{1 + 1} = 𝑥
⇒ 𝑥 = −3/2
Hence, the line segment joining the points 𝐴(1, −5) and 𝐵(−4, 5) is divided by 𝑥−axis at point 𝑃(−3/2, 0) into 1: 1.

6. If (1, 2), (4, y), (x, 6) and (3, 5) are the vertices of a parallelogram taken in order, find x and y.
See SolutionGiven that: Points 𝐴(1, 2), 𝐵(4, 𝑦), 𝐶(𝑥, 6) and 𝐷(3, 5) are vertices of a parallelogram.
The diagonals of parallelogram bisect each other. Therefore Coordinates of mid points of 𝐴𝐶 = Coordinates of mid points of 𝐵𝐷
⇒ ({1 + 𝑥}/2, {2 + 6}/2) = ({3 + 4}/2, {5 + 𝑦}/2)
On comparing {1 + 𝑥/2} = 7/2 and 8/2 = {5 + 𝑦}/2
⇒ 1 + 𝑥 = 7 and 8 = 5 + 𝑦
⇒ 𝑥 = 6 and 𝑦 = 3.

7. Find the coordinates of a point A, where AB is the diameter of a circle whose centre is (2, – 3) and B is (1, 4).
See SolutionHere, AB is the diameter of circle with centre 𝑂(2, −3) and the coordinates of B (1, 4).
Let the coordinates of point A is (𝑥, 𝑦).
The centre 𝑂(2, −3) is the mid-point of the diameter AB, therefore
Coordinates of mid-point of 𝐴𝐵 = Coordinates of point 𝑂
⇒ ({𝑥 + 1}/2, {𝑦 + 4}/2) = (2, −3)
On comparing,
{𝑥 + 1}/2 = 2 and {𝑦 + 4}/2 = −3
⇒ 𝑥 + 1 = 4 and 𝑦 + 4 = −6
⇒ 𝑥 = 3 and 𝑦 = −10
Hence, the coordinates of A is (3, −10).

8. If A and B are (– 2, – 2) and (2, – 4), respectively, find the coordinates of P such that 𝐴𝑃 =3/7 𝐴𝐵 and P lies on the line segment AB.
See SolutionGiven that: 𝐴𝑃 = 3/7𝐴𝐵, therefore, 𝐵𝑃 = 4/7𝐴𝐵
⇒ 𝐴𝑃: 𝑃𝐵 = 3: 4
The point 𝑃 divides the line segment joining the points 𝐴(−2, −2) and 𝐵(2, −4) into 3: 4.
𝐴(−2, −2) 3 𝑃 4 𝐵(2, −4)
Using section formula
({𝑚₁𝑥₂ + 𝑚₂𝑥₁}/{𝑚₁ + 𝑚₂}, {𝑚₁𝑦₂ + 𝑚₂𝑦₁}/{𝑚₁ + 𝑚₂})
The coordinates of 𝑃 is given by
= ({3 × 2 + 4 × (−2)}/{3 + 4}, {3 × (−4) + 4 × (−2)}/{3 + 4})
= (−2/7, −20/7)
Hence, the coordinates of P is (−2/7, −20/7).
9. Find the coordinates of the points which divide the line segment joining A(– 2, 2) and B(2, 8) into four equal parts.
See SolutionLet the points 𝑃, 𝑄 and 𝑅 divides the line segment joining the points 𝐴(−2, 2) and 𝐵(2, 8) in to four equal parts.
𝐴(−2, 2) 1 𝑃 1 Q 1 R 1 𝐵(2, 8)
Therefore, 𝐴𝑃: 𝑃𝐵 = 1: 3
Using section formula
({𝑚₁𝑥₂ + 𝑚₂𝑥₁}/{𝑚₁ + 𝑚₂}, {𝑚₁𝑦₂ + 𝑚₂𝑦₁}/{𝑚₁ + 𝑚₂})
The coordinates of 𝑃 is given by
= ({1 × 2 + 3 × (−2)}/{1 + 3}, {1 × 8 + 3 × 2}/{1 + 3})
= (−4/4, 14/4)
= (−1, 7/2)
Since, 𝐴𝑄: 𝑄𝐵 = 2: 2, therefor the coordinates of point 𝑄 is given by
= ({2 × 2 + 2 × (−2)}/{2 + 2}, {2 × 8 + 2 × 2}/{2 + 2})
= (0/4, 20/4)
= (0, 5)
Since, 𝐴𝑅: 𝑅𝐵 = 3: 1, therefore the coordinates of 𝑄 is given by
= ({3 × 2 + 1 × (−2)}/{3 + 1}, {3 × 8 + 1 × 2}/{3 + 1})
= (4/4, 26/4) = (1, 13/2)
Hence, the points 𝑃(−1, 7/2), 𝑄(0, 5) and 𝑅(1, 13/2) divides AB in four equal parts.

10. Find the area of a rhombus if its vertices are (3, 0), (4, 5), (– 1, 4) and (– 2, – 1) taken in order. [Hint: Area
of a rhombus = 1/2 (product of its diagonals)]
See SolutionThe vertices of rhombus 𝐴𝐵𝐶𝐷 are 𝐴(3, 0), B(4, 5), C(−1, 4) and 𝐷(−2, −1).
Diagonal 𝐴𝐶 = √{(−1 − 3)² + (4 − 0)²} = √(16 + 16) = √32 = 4√2
Diagonal 𝐵𝐷 = √{(−2 − 4)² + (−1 − 5)²} = √(36 + 36) = √72 = 6√2
Area of rhombus = 1/2(Product of two diagonals)
= 1/2 × 𝐴𝐶 × 𝐵𝐷
= 1/2 × 4√2 × 6√2
= 24 square units.

Class 10 Maths Board Questions
1. Find a relation between x and y such that the point P(x, y) is equidistant from the points A (7, 1) and B (3, 5). [CBSE 2024, 2019 (Compartment)
See SolutionFor point P(x, y) to be equidistant from points A(7, 1) and B(3, 5), we need:
PA = PB
√[(x-7)² + (y-1)²] = √[(x-3)² + (y-5)²]
Squaring both sides:
(x-7)² + (y-1)² = (x-3)² + (y-5)²
x² – 14x + 49 + y² – 2y + 1 = x² – 6x + 9 + y² – 10y + 25
x² + y² – 14x – 2y + 50 = x² + y² – 6x – 10y + 34
-14x – 2y = -6x – 10y – 16
-8x + 8y = -16
-x + y = -2
x – y = 2
Therefore, the relation between x and y is x – y = 2.
2. Points A(-1, 1) and B(5, 7) lie on a circle with centre O(2, -3y) such that AB is a diameter of the circle. Find the value of y. Also, find the radius of the circle. [CBSE 2024]
See SolutionSince AB is a diameter, point O is the midpoint of AB.
O(2, -3y) = ((x₁+x₂)/2, (y₁+y₂)/2) = ((-1+5)/2, (1+7)/2) = (2, 4)
So, -3y = 4, which gives y = -4/3
To find the radius, we calculate the distance from O to A (or B):
Radius = OA = √[(2-(-1))² + (4-1)²] = √[3² + 3²] = √[9 + 9] = √18 = 3√2
Therefore, y = -4/3 and the radius of the circle is 3√2 units.
3. Find the ratio in which the line segment joining the points (5, 3) and (-1, 6) is divided by Y-axis. [CBSE 2024]
See SolutionLet the Y-axis intersect the line segment at point P(0, y). Using the formula for a point dividing a line segment internally in the ratio m, If P divides the line segment joining (x₁, y₁) and (x₂, y₂) in ratio m, then:
P = ((mx₂ + nx₁)/(m+n), (my₂ + ny₁)/(m+n))
For the Y-axis, x = 0.
When point P is on the Y-axis, its x-coordinate is 0.
Let’s say P divides the line segment in ratio k:1-k. Then:
0 = (k×(-1) + (1-k)×5)/(k+(1-k))
0 = -k + 5 – 5k
0 = -6k + 5
6k = 5
k = 5/6
Therefore, the Y-axis divides the line segment in the ratio 5:1.
4. In what ratio does the X-axis divide the line segment joining the points (2, -3) and (5, 6)? Also, find the coordinates of the point of intersection.[CBSE 2024]
See SolutionLet the X-axis intersect the line segment at point P(x, 0).
Using the formula for a point dividing a line segment internally in the ratio m , If P divides the line segment joining (x₁, y₁) and (x₂, y₂) in ratio m , then:
P = ((mx₂ + nx₁)/(m+n), (my₂ + ny₁)/(m+n))
For the X-axis, y = 0.
When point P is on the X-axis, its y-coordinate is 0.
Let’s say P divides the line segment in ratio k:1-k. Then:
0 = (k×6 + (1-k)×(-3))/(k+(1-k))
0 = 6k – 3 + 3k
0 = 9k – 3
9k = 3
k = 1/3
The coordinates of P:
x = (k×5 + (1-k)×2)/(k+(1-k))
x = (1/3×5 + 2/3×2)/1
x = (5/3 + 4/3)/1
x = 3
Therefore, the X-axis divides the line segment in the ratio 1:2, and the coordinates of the point of intersection are (3, 0).
5. P(-2, 5) and Q(3, 2) are two points. Find the coordinates of the point R on line segment PQ such that PR = 2QR. [CBSE 2024]
See SolutionIf PR = 2QR, then point R divides PQ externally in the ratio 2:1.
Using the section formula for external division: R = ((m×x₂ – n×x₁)/(m-n), (m×y₂ – n×y₁)/(m-n))
With m = 2, n = 1, x₁ = -2, y₁ = 5, x₂ = 3, y₂ = 2:
R = ((2×3 – 1×(-2))/(2-1), (2×2 – 1×5)/(2-1))
R = ((6 + 2)/1, (4 – 5)/1)
R = (8, -1)
Therefore, the coordinates of point R are (8, -1).
6. In what ratio does the X-axis divide the line segment joining the points (2, -3) and (5, 6)? Also, find the coordinates of the point of intersection. [CBSE 2024]
See SolutionLet the X-axis intersect the line segment at point P(x, 0).
Using the formula for a point dividing a line segment internally in the ratio m,
If P divides the line segment joining (x₁, y₁) and (x₂, y₂) in ratio m, then:
P = ((mx₂ + nx₁)/(m+n), (my₂ + ny₁)/(m+n))
For the X-axis, y = 0.
When point P is on the X-axis, its y-coordinate is 0.
Let’s say P divides the line segment in ratio k:1-k. Then:
0 = (k×6 + (1-k)×(-3))/(k+(1-k))
0 = 6k – 3 + 3k
0 = 9k – 3
9k = 3
k = 1/3
The coordinates of P:
x = (k×5 + (1-k)×2)/(k+(1-k))
x = (1/3×5 + 2/3×2)/1
x = (5/3 + 4/3)/1
x = 3
Therefore, the X-axis divides the line segment in the ratio 1:2, and the coordinates of the point of intersection are (3, 0).
7. Find the length of the median AD of △ABC having vertices A(0, -1), B(2, 1) and C(0, 3). [CBSE 2024]
See SolutionThe median AD connects vertex A to the midpoint D of side BC.
Midpoint D = ((x₂+x₃)/2, (y₂+y₃)/2) = ((2+0)/2, (1+3)/2) = (1, 2)
Length of AD = √[(1-0)² + (2-(-1))²] = √[1² + 3²] = √[1 + 9] = √10
Therefore, the length of the median AD is √10 units.
8. The line segment joining the points A(4, -5) and B(4, 5) is divided by the point P such that AP : AB = 2 : 5. Find the coordinates of P. [CBSE 2023]
See SolutionUsing the section formula, if P divides AB in the ratio m internally, then: P
= ((mx₂ + nx₁)/(m+n), (my₂ + ny₁)/(m+n))
Given that AP : AB = 2 : 5, which means P divides AB in the ratio 2:3
P = [(2×4 + 3×4)/(2+3), (2×5 + 3×(-5)]/(2+3))
P = ((8 + 12)/5, (10 – 15)/5)
P = (20/5, -5/5)
P = (4, -1)
Therefore, the coordinates of P are (4, -1).
9. Point P(x, y) is equidistant from points A(5, 1) and B(1, 5). Prove that x = y. [CBSE 2023]
See SolutionFor point P(x, y) to be equidistant from points A(5, 1) and B(1, 5), we need:
PA = PB
√[(x-5)² + (y-1)²] = √[(x-1)² + (y-5)²]
Squaring both sides:
(x-5)² + (y-1)² = (x-1)² + (y-5)²
x² – 10x + 25 + y² – 2y + 1 = x² – 2x + 1 + y² – 10y + 25
x² + y² – 10x – 2y + 26 = x² + y² – 2x – 10y + 26
-10x – 2y = -2x – 10y
-8x + 8y = 0
-x + y = 0
x = y
Therefore, x = y is proven.
10. Find the ratio in which Y-axis divides the line segment joining the points (5, -6) (-1, -4). [CBSE 2023]
See SolutionLet the Y-axis intersect the line segment at point P(0, y).
Using the formula for a point dividing a line segment internally in the ratio m,
If P divides the line segment joining (x₁, y₁) and (x₂, y₂) in ratio m, then:
P = [(mx₂ + nx₁)/(m+n), (my₂ + ny₁)/(m+n)]
For the Y-axis, x = 0.
When point P is on the Y-axis, its x-coordinate is 0.
Let’s say P divides the line segment in ratio k:1-k. Then:
0 = (k×(-1) + (1-k)×5)/(k+(1-k))
0 = -k + 5 – 5k
0 = -6k + 5
6k = 5
k = 5/6
The y-coordinate of P:
y = (k×(-4) + (1-k)×(-6))/(k+(1-k))
y = (5/6×(-4) + 1/6×(-6))/1
y = (-20/6 – 6/6)/1
y = -26/6 = -13/3
Therefore, the Y-axis divides the line segment in the ratio 5:1, and the coordinates of the point of intersection are (0, -13/3).
11. A line intersects Y-axis and X-axis at point P and Q, respectively. If R(2, 5) is the mid-point of line segment PQ, then find the coordinates of P and Q. [CBSE 2023]
See SolutionLet’s say P(0, a) (since P is on Y-axis, its x-coordinate is 0) and Q(b, 0) (since Q is on X-axis, its y-coordinate is 0).
Given that R(2, 5) is the midpoint of PQ:
2 = (0 + b)/2
5 = (a + 0)/2
Solving:
4 = b
10 = a
Therefore, the coordinates of P are (0, 10) and the coordinates of Q are (4, 0).
12. Find the points on the X-axis, each of which is at a distance of 10 units from the point A(1, -8). [CBSE 2023]
See SolutionLet P(x, 0) be a point on the X-axis.
The distance from A(1, -8) to P(x, 0) is 10 units:
√[(x-1)² + (0-(-8))²] = 10
√[(x-1)² + 64] = 10
Squaring both sides: (x-1)² + 64 = 100
(x-1)² = 36
x-1 = ±6
x = 1±6
x = 7 or x = -5
Therefore, the points on the X-axis are (7, 0) and (-5, 0).
13. Show that the points (-3, -3), (3, 3) and (-3√3, 3√3) are the vertices of an equilateral triangle. [CBSE 2023 Compartment]
See SolutionTo show that a triangle is equilateral, we need to verify that all three sides have the same length.
Let A = (-3, -3), B = (3, 3), and C = (-3√3, 3√3)
Distance AB = √[(3-(-3))² + (3-(-3))²] = √[6² + 6²] = √[36 + 36] = √72 = 6√2
Distance BC = √[((-3√3)-3)² + ((3√3)-3)²]
= √[(-3√3-3)² + (3√3-3)²]
= √[(-(3√3+3))² + (3√3-3)²]
= √[(3√3+3)² + (3√3-3)²]
= √[9(3+√3)² + 9(√3-1)²]
= 3√[(√3+1)² + (√3-1)²]
= 3√[3+2√3+1 + 3-2√3+1]
= 3√[8] = 6√2
Distance CA = √[((-3)-(-3√3))² + ((-3)-(3√3))²]
= √[(-3+3√3)² + (-3-3√3)²]
= √[(3√3-3)² + (-3(1+√3))²]
= √[(3√3-3)² + 9(1+√3)²]
= √[(3√3-3)² + 9(1+√3)²]
= √[(3(√3-1))² + 9(1+√3)²]
= 3√[(√3-1)² + 3(1+√3)²]
= 3√[3-2√3+1 + 3(1+2√3+3)]
= 3√[4 + 3(4+2√3)]
= 3√[4 + 12 + 6√3]
= 3√[16 + 6√3]
= 6√2
Since all three sides have the same length (6√2), the triangle is equilateral.
14. Prove that A(4, 3), B(6, 4), C(5, 6), D(3, 5) are the vertices of a square ABCD.[CBSE 2023 Compartment]
See SolutionTo prove that ABCD is a square, we need to show:
1. All sides have equal length
2. Diagonals are equal in length
3.Diagonals bisect each other
Calculating the side lengths:
AB = √[(6-4)² + (4-3)²] = √[4 + 1] = √5
BC = √[(5-6)² + (6-4)²] = √[1 + 4] = √5
CD = √[(3-5)² + (5-6)²] = √[4 + 1] = √5
DA = √[(4-3)² + (3-5)²] = √[1 + 4] = √5
All sides have the same length (√5), which means ABCD is at least a rhombus.
Calculating the diagonals:
AC = √[(5-4)² + (6-3)²] = √[1 + 9] = √10
BD = √[(3-6)² + (5-4)²] = √[9 + 1] = √10
The diagonals are equal, which confirms that ABCD is a square.
Furthermore, the midpoint of AC and BD:
Midpoint of AC = ((4+5)/2, (3+6)/2) = (4.5, 4.5)
Midpoint of BD = ((6+3)/2, (4+5)/2) = (4.5, 4.5)
The diagonals bisect each other at the same point, confirming that ABCD is a square.
15. Find the ratio in which the point (-1, k) divides the line segment joining the points (-3, 10) and (6, -8). Also, find the value of k. [CBSE 2023 Compartment]
See SolutionLet’s say the point (-1, k) divides the line segment joining (-3, 10) and (6, -8) in the ratio m.
Using the section formula:
(-1, k) = ((m×6 + n×(-3))/(m+n), (m×(-8) + n×10)/(m+n))
From the first coordinate:
-1 = (6m – 3n)/(m+n)
-m – n = 6m – 3n
-m – n = 6m – 3n
-7m = -2n
m = 2n/7
Substituting in the second coordinate:
k = ((-8)×(2n/7) + 10n)/(2n/7 + n)
k = ((-16n/7) + 10n)/(2n/7 + n)
k = ((-16n/7) + 10n)/((2n+7n)/7)
k = ((-16n/7) + 10n)/(9n/7)
k = ((-16n/7) + 10n) × (7/9n)
k = (-16/9) + (70/9)
k = 54/9
k = 6
Therefore, the point divides the line segment in the ratio 2:7 and k = 6.
16. If A(-2, -1), B(a, 0), C(4, b) and D(1, 2) are the vertices of parallelogram ABCD, then find the values of a and b. [CBSE 2023 Compartment]
See SolutionIn a parallelogram, opposite sides are parallel and equal. This means that:
The vector AB is equal to the vector DC
The vector AD is equal to the vector BC
Using the first condition:
AB = DC
(a-(-2), 0-(-1)) = (1-4, 2-b)
(a+2, 1) = (-3, 2-b)
This gives us:
a+2 = -3
a = -5
And 1 = 2-b
b = 1
We can verify using the second condition:
AD = BC
(1-(-2), 2-(-1)) = (4-(-5), 1-0)
(3, 3) = (9, 1)
This doesn’t match, so we need to reconsider. Let’s try with diagonals AC and BD, which should bisect each other in a parallelogram:
The midpoint of AC = ((4+(-2))/2, (b+(-1))/2) = (1, (b-1)/2)
The midpoint of BD = (((-5)+1)/2, (0+2)/2) = (-2, 1)
For these to be equal:
1 = -2
(b-1)/2 = 1
The first equation doesn’t work, so let’s check if ABCD is a parallelogram with vertices in a different order.
Let’s try ABDC (A and C are opposite vertices):
AB = DC
(a-(-2), 0-(-1)) = (1-4, 2-b)
(a+2, 1) = (-3, 2-b)
This gives us:
a+2 = -3
a = -5
And 1 = 2-b
b = 1
Checking with the second condition:
AD = BC
(1-(-2), 2-(-1)) = (4-a, b-0)
(3, 3) = (4-(-5), 1-0)
(3, 3) = (9, 1)
This still doesn’t match, so let’s try ADBC:
AD = BC
(1-(-2), 2-(-1)) = (4-a, b-0)
(3, 3) = (4-a, b)
This gives us:
3 = 4-a
a = 1
And 3 = b
Therefore, a = 1 and b = 3.
17. The three vertices of a parallelogram ABCD, taken in order, are A(-1, 0), B(3, 1) and C(2, 2). Find the coordinates of the fourth vertex D. [CBSE 2023 Compartment]
See SolutionIn a parallelogram, the opposite sides are parallel and equal in length. Also, the diagonals bisect each other.
Using the fact that diagonals bisect each other, we have:
Midpoint of AC = Midpoint of BD
((A₁+C₁)/2, (A₂+C₂)/2) = ((B₁+D₁)/2, (B₂+D₂)/2)
Midpoint of AC = ((-1+2)/2, (0+2)/2) = (1/2, 1)
Therefore: (1/2, 1) = ((3+D₁)/2, (1+D₂)/2)
1/2 = (3+D₁)/2
1 = (1+D₂)/2
This gives us:
1/2 = (3+D₁)/2
D₁ = 1/2 – 3 = -2.5 = -5/2
And 1 = (1+D₂)/2
D₂ = 2×1 – 1 = 1
Therefore, the coordinates of the fourth vertex D are (-5/2, 1).
18. Show that the four points A(0, -1), B(6, 7), C(-2, 3) and D(8, 3) are the vertices of a rectangle ABCD. [CBSE 2023 Compartment]
See SolutionTo prove that ABCD is a rectangle, we need to show:
1. Opposite sides are parallel and equal (i.e., it’s a parallelogram)
2. One of the angles is 90° (or equivalently, adjacent sides are perpendicular)
Checking for a parallelogram:
Vector AB = (6-0, 7-(-1)) = (6, 8)
Vector DC = (8-(-2), 3-3) = (10, 0)
Vector AD = (0-8, -1-3) = (-8, -4)
Vector BC = (6-(-2), 7-3) = (8, 4)
Since AB ≠ DC and AD ≠ BC, ABCD is not a parallelogram with these vertices in this order.
Let’s try ABDC:
Vector AB = (6-0, 7-(-1)) = (6, 8)
Vector DC = (-2-8, 3-3) = (-10, 0)
These aren’t parallel, so ABCD is not a parallelogram with vertices in this order either.
Let’s try ADBC:
Vector AD = (8-0, 3-(-1)) = (8, 4)
Vector BC = (-2-6, 3-7) = (-8, -4)
Vector AB = (6-0, 7-(-1)) = (6, 8)
Vector DC = (8-(-2), 3-3) = (10, 0)
The vectors AD and BC are negative of each other, which means they are parallel and equal in magnitude but opposite in direction.
Let’s check if the vertices are in order ACBD:
Vector AC = (-2-0, 3-(-1)) = (-2, 4)
Vector BD = (8-6, 3-7) = (2, -4)
Vector AB = (6-0, 7-(-1)) = (6, 8)
Vector CD = (8-(-2), 3-3) = (10, 0)
AC and BD are negative of each other, which means ACBD forms a parallelogram.
Now let’s check for perpendicular sides to determine if it’s a rectangle:
Dot product of AC and AB = (-2)×6 + 4×8 = -12 + 32 = 20
Since the dot product is not zero, these sides are not perpendicular.
Let’s check with points in order ABCD:
Vector AB = (6-0, 7-(-1)) = (6, 8)
Vector AD = (8-0, 3-(-1)) = (8, 4)
Dot product of AB and AD = 6×8 + 8×4 = 48 + 32 = 80
These are not perpendicular either.
Let me re-verify the distances between points to see if they form a rectangle with a different ordering:
AB = √[(6-0)² + (7-(-1))²] = √[36 + 64] = √100 = 10
BC = √[(-2-6)² + (3-7)²] = √[64 + 16] = √80 = 4√5
CD = √[(8-(-2))² + (3-3)²] = √[100 + 0] = 10
DA = √[(0-8)² + (-1-3)²] = √[64 + 16] = √80 = 4√5
Diagonals: AC = √[(-2-0)² + (3-(-1))²] = √[4 + 16] = √20 = 2√5
BD = √[(8-6)² + (3-7)²] = √[4 + 16] = √20 = 2√5
With this ordering, opposite sides are equal (AB = CD and BC = DA) and diagonals are equal (AC = BD), which means ABCD forms a rectangle.
19. Show that the points A(6, 4), B(5, -2), C(7, -2) are the vertices of an isosceles triangle. Also, find the length of the median through point A. [CBSE 2023 Compartment]
See SolutionTo show that triangle ABC is isosceles, we need to show that at least two sides are equal.
AB = √[(5-6)² + (-2-4)²] = √[1 + 36] = √37
BC = √[(7-5)² + (-2-(-2))²] = √[4 + 0] = 2
CA = √[(6-7)² + (4-(-2))²] = √[1 + 36] = √37
Since AB = CA, triangle ABC is isosceles.
To find the length of the median through point A:
The median from A connects A to the midpoint D of BC.
Midpoint D = ((5+7)/2, (-2+(-2))/2) = (6, -2)
The length of median AD = √[(6-6)² + (-2-4)²] = √[0 + 36] = 6
Therefore, the length of the median through point A is 6 units.
20. A circle has its centre at (4, 4). If one end of a diameter is (4, 0), then find the coordinates of the other end. [CBSE 2020 Compartment]
See SolutionIf (4, 4) is the center of the circle and (4, 0) is one end of a diameter, then the other end of the diameter is located on the opposite side of the center at the same distance.
The distance from center to (4, 0) is √[(4-4)² + (4-0)²] = √[0 + 16] = 4
So, the other end of the diameter is also 4 units from the center, but in the opposite direction. Vector from center to first endpoint = (4-4, 0-4) = (0, -4)
Vector from center to second endpoint = (0, 4)
Therefore, the coordinates of the other end of the diameter are (4, 8).
21. Find the ratio in which the line segment joining the points A(6, 3) and B(-2, -5) is divided by X-axis. [CBSE 2020]
See SolutionLet’s say the X-axis (y = 0) intersects the line segment AB at point P(x, 0).
Using the section formula, if P divides AB in the ratio k:1-k internally, then:
P = ((k×(-2) + (1-k)×6)/(k+(1-k)), (k×(-5) + (1-k)×3)/(k+(1-k)))
P = ((-2k + 6-6k)/1, (-5k + 3-3k)/1)
P = (-8k + 6, -8k + 3)
Since P lies on the X-axis, its y-coordinate is 0:
-8k + 3 = 0
-8k = -3
k = 3/8
The ratio in which the X-axis divides the line segment is k:(1-k) = 3/8 : 5/8 = 3:5.
22. If the point C(-1, 2) divides internally the line segment joining A(2, 5) and B(x, y) in the ratio 3:4, find the coordinates of B. [CBSE 2020]
See SolutionSince C(-1, 2) divides AB internally in the ratio 3:4, we can use the section formula:
C = ((3×x + 4×2)/(3+4), (3×y + 4×5)/(3+4))
(-1, 2) = ((3x + 8)/7, (3y + 20)/7)
Equating the coordinates:
-1 = (3x + 8)/7
2 = (3y + 20)/7
Solving for x:
-7 = 3x + 8
-15 = 3x
x = -5
Solving for y:
14 = 3y + 20
-6 = 3y
y = -2
Therefore, the coordinates of B are (-5, -2).
23. If the mid-point of the line segment joining the points A(3, 4) and B(k, 6) is P(x, y) and x + y – 10 = 0, then find the value of k. [CBSE 2020]
See SolutionThe mid-point of AB is:
P(x, y) = ((3+k)/2, (4+6)/2) = ((3+k)/2, 5)
Since P lies on the line x + y – 10 = 0, we have:
(3+k)/2 + 5 – 10 = 0
(3+k)/2 – 5 = 0
3+k = 10
k = 7
Therefore, the value of k is 7.
24. Write the coordinates of a point P on X-axis which is equidistant from the points A(−2, 0) and B(6, 0). [CBSE 2019]
See SolutionSince point P lies on the X-axis, its coordinates are P(x, 0) for some value of x.
For P to be equidistant from A(−2, 0) and B(6, 0):
|PA| = |PB|
|x − (−2)| = |x − 6|
|x + 2| = |x − 6|
There are two cases to consider:
1. If x + 2 ≥ 0 and x − 6 ≥ 0: x + 2 = x − 6 2 = −6 (contradiction)
2. If x + 2 ≥ 0 and x − 6 < 0: x + 2 = −(x − 6) x + 2 = −x + 6 2x = 4 x = 2
3. If x + 2 < 0 and x − 6 ≥ 0: −(x + 2) = x − 6 −x − 2 = x − 6 −2x = −4 x = 2
4. If x + 2 < 0 and x − 6 < 0: −(x + 2) = −(x − 6) −x − 2 = −x + 6 −2 = 6 (contradiction)
The only valid solution is x = 2. Therefore, the coordinates of point P are (2, 0).
25. Find the ratio in which the segment joining the points (1, −3) and (4, 5) is divided by X-axis? Also, find the coordinates of this point on X-axis. [CBSE 2019]
See SolutionThe X-axis has equation y = 0.
Let’s say the X-axis divides the line segment in ratio m.
If P is the point of intersection, then P = (x, 0) for some x.
Using the section formula:
P = (x, 0) = ((m×4 + n×1)/(m+n), (m×5 + n×(−3))/(m+n))
From the y-coordinate:
0 = (5m − 3n)/(m+n)
5m − 3n = 0
5m = 3n
m = 3:5
To find the x-coordinate of P, substitute m = 3n/5 into the x-coordinate formula:
x = ((3n/5)×4 + n×1)/((3n/5)+n)
= (12n/5 + n)/((3n/5)+n)
= (12n/5 + n)/((3n+5n)/5)
= (12n/5 + n)/(8n/5)
= 5(12n/5 + n)/(8n)
= (12n + 5n)/(8n)
= 17n/(8n)
= 17/8
Therefore, the X-axis divides the line segment joining (1, −3) and (4, 5) in the ratio 3:5, and the point of intersection is (17/8, 0).
26. Find the coordinates of a point A, where AB is diameter of a circle whose centre is C(2, −3) and B is the point (1, 4). [CBSE 2019]
See SolutionIf AB is a diameter of a circle with center C, then C is the midpoint of AB.
Let the coordinates of A be (x, y). Since C is the midpoint of AB:
C = ((x+1)/2, (y+4)/2)
(2, −3) = ((x+1)/2, (y+4)/2)
From the x-coordinate:
2 = (x+1)/2
4 = x+1
x = 3
From the y-coordinate:
−3 = (y+4)/2
−6 = y+4
y = −10
Therefore, the coordinates of point A are (3, −10).
27. Find the coordinates of a point A, where AB is a diameter of the circle with centre (−2, 2) and B is the point with coordinates (3, 4). [CBSE 2019]
See SolutionIf AB is a diameter of a circle with center C(−2, 2), then C is the midpoint of AB.
Let the coordinates of A be (x, y). Since C is the midpoint of AB:
C = ((x+3)/2, (y+4)/2) (−2, 2)
= ((x+3)/2, (y+4)/2)
From the x-coordinate:
−2 = (x+3)/2
−4 = x+3
x = −7
From the y-coordinate:
2 = (y+4)/2
4 = y+4
y = 0
Therefore, the coordinates of point A are (−7, 0).
28. In what ratio is the line segment joining the points P(3, −6) and Q(5, 3) divided by X-axis? [CBSE 2019 Compartment]
See SolutionThe X-axis has equation y = 0.
Let’s say the X-axis divides the line segment in ratio m.
If R is the point of intersection, then R = (x, 0) for some x.
Using the section formula:
R = (x, 0) = ((m×5 + n×3)/(m+n), (m×3 + n×(−6))/(m+n))
From the y-coordinate:
0 = (3m − 6n)/(m+n)
3m − 6n = 0
3m = 6n
m = 2:1
To find the x-coordinate of R, substitute m = 2n into the x-coordinate formula:
x = ((2n)×5 + n×3)/((2n)+n)
= (10n + 3n)/(3n)
= 13n/(3n)
= 13/3
Therefore, the X-axis divides the line segment joining P(3, −6) and Q(5, 3) in the ratio 2:1, and the point of intersection is (13/3, 0).
29. If A(−2, 2), B(5, 2) and C(k, 8) are the vertices of a right-angled △ABC with ∠B = 90°, then find the value of k. [CBSE 2019 Compartment]
See SolutionFor a triangle to have a right angle at B, the sides AB and BC must be perpendicular to each other.
AB = (5 − (−2), 2 − 2) = (7, 0)
BC = (k − 5, 8 − 2) = (k−5, 6)
For AB ⊥ BC, their dot product must be zero:
AB·BC = 7(k−5) + 0(6) = 0
7(k−5) = 0
k = 5
Therefore, k = 5.
30. Find the ratio in which the Y-axis divides the line segment joining the points (−1, −4) and (5, −6). Also, find the coordinates of the point of intersection. [CBSE 2019]
See SolutionThe Y-axis has equation x = 0.
Let’s say the Y-axis divides the line segment in ratio m.
If P is the point of intersection, then P = (0, y) for some y.
Using the section formula:
P = (0, y) = ((m×5 + n×(−1))/(m+n), (m×(−6) + n×(−4))/(m+n))
From the x-coordinate:
0 = (5m − n)/(m+n)
5m = n
m = 1:5
To find the y-coordinate of P, substitute n = 5m into the y-coordinate formula:
y = (m×(−6) + 5m×(−4))/((m)+5m)
= (−6m − 20m)/(6m)
= −26m/(6m)
= −26/6
= −4.33
Therefore, the Y-axis divides the line segment joining (−1, −4) and (5, −6) in the ratio 1:5, and the point of intersection is (0, −4.33).
31. Find the point on Y-axis which is equidistant from the points (5, −2) and (−3, 2). [CBSE 2019]
See SolutionLet P(0, y) be the point on the Y-axis that is equidistant from A(5, −2) and B(−3, 2).
Then:
|PA| = |PB|
|PA|² = |PB|²
(0−5)² + (y−(−2))² = (0−(−3))² + (y−2)²
25 + (y+2)² = 9 + (y−2)²
25 + y² + 4y + 4 = 9 + y² − 4y + 4
25 + 4y = 9 − 4y
8y = −16
y = −2
Therefore, the coordinates of the point on the Y-axis are (0, −2).
32. The line segment joining the points A(2, 1) and B(5, −8) is trisected at the points P and Q such that P is nearer to A. If P also lies on the line given by 2x − y + k = 0, find the value of k. [CBSE 2019]
See SolutionSince the line segment AB is trisected at points P and Q, and P is nearer to A, then:
AP:PQ
= 1:1:1, or AP
= 1:3
This means P divides AB in the ratio 1:2.
Using the section formula for P:
P = ((1×5 + 2×2)/(1+2), (1×(−8) + 2×1)/(1+2))
= ((5 + 4)/3, (−8 + 2)/3)
= (9/3, −6/3)
= (3, −2)
Now, since P lies on the line 2x − y + k = 0, we have:
2(3) − (−2) + k = 0
6 + 2 + k = 0
8 + k = 0
k = −8
Therefore, the value of k is −8.
Class 10 Math solutions, especially the ones in exercise 7.1 and exercise 7.2, simplify complex problems into manageable steps, ensuring clarity for students. For those looking for quick access, Class 10 Maths Chapter 7 NCERT Textbook solutions PDF provides convenient offline learning. The Coordinate Geometry Class 10 solutions PDF format is highly sought after by students preparing for exams. Mastery of Class 10 Math Chapter 7 formulas is critical, as they form the basis for solving real-world problems. With structured question answers, these solutions serve as a comprehensive guide for effective preparation.
Class 10th Maths Chapter 7 Exercise 7.1 Solutions
10th Maths Chapter 7 Exercise 7.2 Solutions
Class 10th Maths Chapter 7 Solutions for State Boards
Benefits of NCERT Solutions for Class 10 Coordinate Geometry
Class 10 Mathematics NCERT Textbook Solutions for Coordinate Geometry offer a step-by-step approach to tackle problems efficiently, catering to students of all learning paces. By practicing Class 10 NCERT Maths Chapter 7 important questions, students can strengthen their understanding of key topics. Maths Exercises like 7.3 and 7.4 delve deeper into advanced problems, fostering analytical thinking. The Coordinate Geometry Class 10th NCERT Book solutions also include detailed explanations for every question, ensuring no doubts remain unresolved.
Downloadable formats like NCERT solutions for Class 10 Math Chapter 7 PDF provide the flexibility to study anytime, anywhere. Whether it’s grasping the derivation of the midpoint formula or solving challenging section formula problems, these solutions are tailored for conceptual clarity. Students frequently use Coordinate Geometry Class 10 Mathematics formulas while solving critical questions, making them indispensable for exam preparation.
Important Points for Class 10 Maths Chapter 7 Coordinate Geometry
Key points in Class 10 Maths Chapter 7 Coordinate Geometry include the distance formula, section formula and area of a triangle formula. Focus on deriving coordinates, dividing line segments and applying these concepts to solve real-life problems. Practice NCERT exercises 7.1 and 7.2 thoroughly for board exam preparation.
| Day | Topic | Activity | Objective |
|---|---|---|---|
| Day 1 | Introduction to Coordinate Geometry | Read NCERT textbook and notes | Understand basic concepts |
| Day 2 | Distance Formula | Practice NCERT Exercise 7.1 | Learn to calculate distances |
| Day 3 | Section Formula | Practice NCERT Exercise 7.2 | Understand division of line segments |
| Day 4 | Area of a Triangle | Practice NCERT Exercise 7.3 | Calculate areas using coordinates |
| Day 5 | Revision and Important Questions | Solve NCERT Exercise 7.4 | Review and strengthen concepts |
| Day 6 | Mock Tests | Attempt sample papers | Evaluate preparation and improve |
| Class: 10 | Maths |
| Chapter 7: | Coordinate Geometry |
| Content: | NCERT Exercises Solutions |
| Mode: | Online Videos and Text Format |
| Academic Session: | Year 2025-26 |
| Medium: | English and Hindi Medium |
Leveraging NCERT Solutions for Academic Excellence
The NCERT Mathematics Solutions for Class 10 Chapter 7 exercise solutions are crafted to align with the CBSE curriculum, ensuring students excel in exams. By working through the Coordinate Geometry Class 10 important questions, students not only practice but also enhance their speed and accuracy. Comprehensive notes for Class 10 Maths Chapter 7 cover formulas, problem-solving techniques, and real-life applications of Coordinate Geometry. These solutions simplify the intricacies of topics like the distance formula, helping students develop a thorough understanding.
The Class 10 Math Book Chapter 7 question answers are particularly beneficial for last-minute revisions, ensuring all critical points are covered. For in-depth practice, students rely on the NCERT Book solutions for Class 10 Mathematics Chapter 7 exercise 7.1 to 7.4, which address varying difficulty levels. By mastering these resources, students build a solid foundation for higher math.
Class 10 Maths chapter 7 Coordinate Geometry Solution
Class 10 Maths Chapter 7 Exercises Solution is useful for UP Board as well as CBSE, MP Board Schools in Hindi Medium and English medium in PDF format to free download. UP Board High School students are now using NCERT Books for school exams. Download UP Board Solutions and NCERT Solutions Apps 2025-26 based on updated NCERT Solutions for the new session 2025-26. There is overall summery about coordinate geometry for class 10, which will help the students to know more about this chapter.
10th Maths Chapter 7 Previous Years Questions
ONE MARK QUESTIONS
1. If the distance between the points (4, k) and (1, 0) is 5, then what can be the possible values of k? [CBSE 2017]
THREE MARKS QUESTIONS
1. The area of a triangle is 5 sq units. Two of its vertices are (2, 1) and (3, -2). If the third vertex is (7/2, y), find the value of y. [CBSE 2017]
2. Show that triangle ABC, where A(-2, 0), B(2, 0), C(0, 2) and triangle PQR where (-4, 0), Q(4, 0), R(0, 4) are similar triangles. [CBSE 2017]
FOUR MARKS QUESTIONS
1. If a≠b≠0, prove that the points (a, a²), (b, b²), (0, 0) will not be collinear. [CBSE 2017]
Know about Coordinate Geometry
In Coordinate geometry, we study that the distance of a point from the y-axis is called its x-coordinate, or abscissa (abscissa is a Latin word which means cut off) and the distance of a point from the x-axis is called its y-coordinate, or ordinate (ordinate is a Latin word which means keep it in order). Abscissa and ordinate collectively forms coordinate of a point in Cartesian system. The coordinates of a point on the x-axis are of the form (x, 0), and of a point on the y-axis are of the form (0, y). For more question on coordinate geometry, go through NCERT exemplar problems for Class 10 Maths.
Historical Facts! about Coordinate Geometry
Rene Descartes (1596 – 1650) was a French philosopher, mathematician whose work ‘La geometrie’ includes his application of algebra to geometry from which we now have Cartesian geometry.
What are the key topics covered in NCERT Solutions for Class 10 Maths Chapter 7 Coordinate Geometry?
The NCERT Detailed Solutions for Class 10 Mathematics Chapter 7 Coordinate Geometry focus on essential topics such as the distance formula, section formula and finding the coordinates of a point dividing a line segment in a given ratio. 10th Math Chapter 7 solutions also explain how to determine the area of a triangle using coordinate points and apply these concepts to real-world problems. Exercises like 7.1 to 7.4 cover basic to advanced-level problems, ensuring a comprehensive understanding. By mastering these concepts, students build a strong mathematical foundation necessary for higher studies and competitive exams.
What is the main objective of Chapter 7 Coordinate Geometry in class 10 Maths?
Objectives of Coordinate Geometry
To find the distance between two different points whose co-ordinates are given and finding the co-ordinates of a point, which divides the line segment joining two points in a given ratio internally. To find the co-ordinates of the mid-point of the join of two points to get the co-ordinates of the centroid of a triangle with given vertices.
How can students benefit from Class 10 Maths Chapter 7 NCERT Solutions PDF?
The Class 10 Mathematics Chapter 7 NCERT Book Solutions PDF offers a convenient way for students to access solutions offline, making it easier to revise and practice anytime. These solutions provide step-by-step answers to all textbook exercises, including important questions and formulas like the midpoint and section formulas. By practicing through this PDF, students can strengthen their conceptual clarity, improve their problem-solving speed and prepare effectively for exams. The structured format ensures students grasp the logic behind each solution, making it an indispensable resource for thorough preparation.
How can one get good marks in class 10 Chapter 7 Maths?
For examination purpose, we have to do only first three exercises. Exercise 7.4 is an optional one, given only for extra practice. Out of exercise 7.1, and 7.2, if a student complete the first exercise thoroughly he can score good marks in entire chapter 7 of class 10 Maths.
How are NCERT Solutions for Coordinate Geometry helpful for exam preparation?
NCERT Detailed Solutions for Coordinate Geometry are designed to align perfectly with the CBSE curriculum, ensuring students are well-prepared for exams. These solutions simplify complex problems using clear explanations and examples, making even the most challenging topics easy to understand. By practicing Class 10 Mathematics Chapter 7 important questions and revising the formulas, students gain confidence in solving coordinate geometry problems. The solutions also focus on critical exercises like 7.1 to 7.2, covering questions of varying difficulty levels to enhance analytical thinking and accuracy. This makes the resource an essential tool for scoring well in exams.
What are the Important Results in Chapter 7 Class 10 Maths Coordinate Geometry?
Based on class 10 Maths Chapter 7, the Important Results in Coordinate Geometry are as follows:
1. The co-ordinates of the origin are (0, 0)
2. The y co-ordinate of every point on the x-axis is 0 and the x co-ordinate of every point on the y-axis is 0.
3. The two axes XOX’ and YOY’ divide the plane into four parts called quadrants.
Why is mastering Class 10 Maths Chapter 7 formulas important?
Formulas in Class 10 Maths Chapter 7 form the backbone of solving problems in Coordinate Geometry. Key formulas such as the distance formula, section formula and the area of a triangle help students tackle various types of questions. Mastering these formulas allows students to solve problems quickly and efficiently during exams. The NCERT Textbook solutions for Class 10 Maths Chapter 7 exercise solutions ensure students practice these formulas extensively across different scenarios. By incorporating these formulas into their problem-solving routine, students improve their understanding, enhance accuracy and develop confidence in handling higher-level mathematics.
What are the important examples of class 10 Maths chapter 7 Coordinate Geometry?
Example number 4, 5, 9, 10 and 14 are considered as important examples of 10th Maths Chapter 7 Coordinate Geometry as these are frequently asked in board exams as well as school tests.
What are the main topics to study in chapter 7 Coordinate Geometry Class 10 Maths?
In chapter 7 (Coordinate Geometry) of class 10th math, Students will study:
1) Distance Formula (To find distance between two points P(x₁, y₁) and Q(x₂, y₂)).
2) Section Formula.
How many exercises are there in chapter 7 of 10 Maths?
There are 2 exercises (exercise 7.1, and 7.2) in chapter 7 (Coordinate Geometry) of class 10 Maths and exercise 7.3 and 7.4 are now deleted from syllabus.
Does chapter 7 (Coordinate Geometry) of class 10 math contain any Theorem?
No, chapter 7 (Coordinate Geometry) of class 10 math doesn’t contain any Theorem.


