NCERT Detailed Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry in English and Hindi Medium for CBSE 2025-26 Exams. NCERT Class 10 Math Textbook chapter 8 is revised as per the CBSE Mathematics books published for Academic Session 2025-26. The Introduction to Trigonometry NCERT Class 10 chapter is a cornerstone of the CBSE curriculum, setting the stage for understanding higher mathematical concepts. NCERT 10th Math chapter 8 focuses on the fundamentals of trigonometric ratios like sine, cosine and tangent, which form the backbone of trigonometric calculations. Students can refer to Class 10 Mathematics Chapter 8 Exercise Solutions to grasp these concepts and solve trigonometry problems step by step.
Class 10 Mathematics Chapter 8 NCERT Textbook Solutions
The chapter also introduces real-life applications of these ratios, ensuring students comprehend their practical relevance. The Class 10 Trigonometry Formulas provided in the NCERT textbook are essential tools for solving exercises. By practicing the Class 10 Mathematics Chapter 8 Important Questions, students can enhance their problem-solving skills and build confidence. The NCERT Detailed Solutions for Class 10 Math Chapter 8 in PDF format make it easy for learners to access study material anytime, aiding their preparation effectively.
Class 10 Maths Chapter 8 Exercise 8.1 Solutions
Class 10 Maths Chapter 8 Exercise 8.2 Solutions
Class 10 Maths Chapter 8 Exercise 8.3 Solutions
10th Maths Chapter 8 Solutions for State Boards
Trigonometric Identities and Their Applications
A significant portion of the Class 10 Trigonometry syllabus revolves around trigonometric identities, which are vital for simplifying complex equations. These identities form the basis of solving intricate problems found in the Class 10 Mathematics Chapter 8 Exercises. The NCERT Trigonometry Solutions guide students through the logical steps of deriving and applying these identities, making them easier to comprehend. Accessing the Class 10 Maths Book Chapter 8 PDF ensures that students have a reliable resource to review formulas and explanations.
Solving the NCERT Book Class 10 Trigonometry Questions not only helps in mastering the chapter but also prepares students for competitive exams. The Class 10 Maths Chapter 8 Study Material, which includes detailed explanations and NCERT Class 10 Math Solutions PDF, is an invaluable asset for reinforcing conceptual clarity and application-based learning.
Important Points for Class 10 Maths Chapter 8 Introduction to Trigonometry
Trigonometric Ratios: Sine, Cosine, Tangent, and their reciprocals.
Trigonometric Identities: Fundamental identities and their derivations.
Value of Ratios: For angles 0°, 30°, 45°, 60°, 90°.
Application: Problems involving heights and distances.
Practice Questions: Focus on NCERT exercises and examples.
| Day | Topic | Task |
|---|---|---|
| Day 1 | Introduction to Trigonometry | Understand basic trigonometric ratios and definitions (sine, cosine, tangent). |
| Day 2 | Trigonometric Ratios for Standard Angles | Learn the values of trigonometric ratios for 0°, 30°, 45°, 60°, and 90°. |
| Day 3 | Trigonometric Identities | Practice derivations and applications of key trigonometric identities. |
| Day 4 | Exercise Questions | Solve NCERT exercise problems for trigonometric ratios and identities. |
| Day 5 | Application: Heights and Distances | Understand real-life applications and solve related problems from the textbook. |
| Day 6 | Revision | Revise key formulas, concepts, and solve mock test papers. |
| Class: 10 | Mathematics |
| Chapter 8: | Introduction to Trigonometry |
| Content Type: | Text, Videos and PDF |
| Contents: | NCERT Textbook Solutions |
| Session: | CBSE 2025-26 |
| Medium: | Hindi and English medium |
Effective Preparation for Chapter 8 Trigonometry
To excel in the Introduction to Trigonometry Class 10 chapter, students should focus on regular practice and thorough understanding of concepts. Referring to the Class 10 Maths Chapter 8 Notes simplifies the revision process, highlighting the key topics and formulas. Practicing the NCERT Class 10 Math Trigonometry Chapter Solutions provided in the NCERT Solutions for Class 10 Mathematics Textbook Chapter 8 PDF Download enhances problem-solving speed and accuracy.
It’s also beneficial to attempt the Class 10 Maths Chapter 8 Practice Questions to identify weak areas and improve. These resources, including the NCERT Book Class 10 Maths Trigonometry PDF, are designed to make learning accessible and engaging for students. By mastering the trigonometric identities, ratios and their applications, students can ensure a strong foundation in mathematics, paving the way for academic success in exams and beyond.
Class 10 Maths Chapter 8 Introduction to Trigonometry Solution
Class 10 Maths Chapter 8 Solutions are updated for current academic session 2025-26 based on NCERT Books. UP Board students are also using NCERT Textbooks for their exams now. So, they also can download UP Board Solutions for Class 10 Maths Chapter 8 Solutions in Hindi Medium from this page. Solutions are given in videos format also describing in English and Hindi.

NCERT Solutions and Offline apps for UP Board and CBSE Board are also given free to download. Download Offline as well as Online Apps based on updated NCERT Solutions based on latest NCERT books 2025-26. Revision books are also available to download. Description, history and identities related to Trigonometry is given below.
10th Maths Chapter 8 Solutions
NCERT Updated Solutions for class 10 Maths Chapter 8 Introduction to Trigonometry for Session 2025-26 exercises from 8.1 to 8.3 are given to use online or download in PDF format free. These solutions are in Hindi and English Medium format. If you have any doubt, please visit to Discussion Forum to ask your doubts.

Historical Facts!
1. The creator of trigonometry is said to have been the Greek Mathematician Hipparchus of the 2nd century BC.
2. The word Trigonometry which means triangle measurement is credited to Bastholoman Pitiscus (1561-1613).
3. The first use of the idea of ‘sine’ can be found in the work of ‘Aryabhatiyam’ of Aryabhata in 500 AD. Aryabhata used the word Ardha-jya for the half-chord, which was shortened to Jya or Jiva in due course. When the Aryabhatiyam was translated into Arabic, the word Jiva was retained. It was further translated into ‘Sinus’, which means curve in Latin. The word ‘Sinus’ also used as sine was first abbreviated and used as ‘sin’ by an English professor of astronomy Edmund Gunter (1581-1626).
4. The origin of the terms ‘Cosine’ and ‘tangent’ was much later. The cosine function arose from the need to compute the sine of the complementary angle. Aryabhata called it Kotijya. The name cosinus originated with Edmund Gunter. In 1674, another English mathematician Sir Jonas Moore first used the abbreviated notation ‘cos’.
Trigonometric Identities
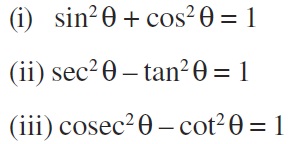
Trigonometric Ratios
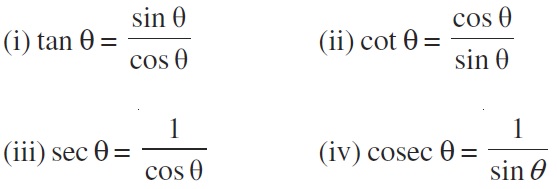
What are the key topics covered in NCERT Class 10 Maths Chapter 8 Introduction to Trigonometry?
NCERT Class 10 Maths Chapter 8 Introduction to Trigonometry primarily focuses on trigonometric ratios like sine, cosine and tangent, along with their relationships. Students learn about the fundamental trigonometric identities, which are essential for solving equations. The chapter also delves into the application of these ratios in real-life scenarios, such as measuring heights and distances. It emphasizes conceptual clarity through Class 10 Math Trigonometry Exercises and provides practical applications of mathematical formulas. To assist students, NCERT Trigonometry Solutions explain the derivations and methods step by step, making it easier to solve complex problems systematically.
How many exercise wise questions are there in class 10 Maths chapter 8?
There are 4 exercises in class 10 math chapter 8 Introduction to Trigonometry.
In first exercise (Ex 8.1), there are in all 11 questions.
In second exercise (Ex 8.2), there are in all 4 questions.
In third exercise (Ex 8.3), there are 5 questions.
So, there are in all 20 questions in class 10 math chapter 8 Introduction to Trigonometry.
There are in all 15 examples in class 10 math chapter 8 Introduction to Trigonometry.
Examples 1, 2, 3, 4, 5 are based on Ex 8.1.
Examples 6, 7, 8 are based on Ex 8.2.
Examples 12, 13, 14, 15 are based on Ex 8.3.
How can NCERT Solutions for Class 10 Maths Chapter 8 help in exam preparation?
The NCERT Textbook Solutions for Class 10 Maths Chapter 8 are tailored to enhance a student’s understanding of trigonometry. These solutions provide detailed explanations for each exercise, helping students grasp difficult concepts like trigonometric ratios and identities with ease. They also offer shortcuts and tips for solving problems faster, which is especially helpful for exams. Practicing through the solutions ensures that students are well-prepared for both school and competitive exams. The availability of solutions in PDF format makes them accessible, allowing students to revise anytime. Regular practice with these solutions builds confidence and improves overall problem-solving skills.
What are the important examples from chapter 8 class 10 math?
Examples given in NCERT books are always important for CBSE exams. Examples 3, 4, 5, 7, 8, 10, 11, 13, 14 and 15 of chapter 8 (Introduction to Trigonometry) of class 10 math are the important examples from exam point of view. In exam questions can come from these examples.
What resources are available for mastering Class 10 Trigonometry?
Students can access a variety of resources to master Class 10 Trigonometry, including Class 10 Maths Chapter 8 Notes, Practice Questions and NCERT Book Solutions in PDF format. These resources offer step-by-step explanations, textbook solved examples and comprehensive solutions for every exercise in the chapter. The Class 10 Trigonometry Formulas and Important Questions help students focus on key concepts during revision. Study material such as mock tests and chapter summaries aid in thorough preparation. By utilizing these tools, students can strengthen their understanding of trigonometric concepts and perform well in exams.
Which are the main topics students go through in chapter 8 of class 10th Mathematics?
In chapter 8 Introduction to Trigonometry of class 10th math, Students will study:
1) Trigonometric Ratios.
2) Trigonometric Ratios of Some Specific Angles.
3) Trigonometric Identities.
This chapter is very interesting. Also this chapter is completely new for students.
How are trigonometric identities useful in solving problems in Chapter 8?
Trigonometric identities are foundational for solving complex equations in Class 10 Mathematics Chapter 8 Introduction to Trigonometry. These identities simplify expressions and allow students to relate different trigonometric ratios easily. By mastering these formulas, students can solve challenging problems efficiently, including those involving heights and distances. The NCERT Trigonometry Solutions provide clear explanations on how to derive and apply these identities in various exercises. Practicing these identities using the Class 10 Math Chapter 8 Exercises sharpens analytical skills and prepares students for exams. Understanding their application is crucial for tackling advanced topics in higher mathematics.
Why is chapter 8 of Class 10th Maths important?
Chapter 8 (Introduction to Trigonometry) of 10th Math is important because there is a chapter in class 11th math named Trigonometric functions and chapter 8 (Introduction to Trigonometry) of 10th Math works as a base for that chapter. Also from exam point of view chapter 8 (Introduction to Trigonometry) of 10th Math is very important. Every year 7-8 marks questions come from this chapter.
What do you learn about Trigonometry in Class 10 Maths Chapter 8?
Trigonometry is the oldest branch of mathematics. This concept was first used by Aryabhata in Aryabhatiyam in 500 A.D. Trigonometry is a word consisting of three Greek words: Tri-Gon-Metron. ‘Tri’ means three, ‘Gon’ means side and ‘Metron’ means measure. So, trigonometry is the study related to the measure of sides and angles of a triangle in particular, right triangles (in CBSE class 10).
How can I score more that 90% in class 10 Maths Chpater 8 Trigonometry?
To score well in trigonometry, we should practice hard the entire chapter 8 in 10th Maths. Specially exercise 8.4 needs more time to spend for solving the questions based on identities. All the parts of question 5 of exercise 8.4 asked in exams frequently.
Is there any application of trigo as a tool in astronomy for Class 10 Mathematics 8th Chapter?
Trigonometry is used in astronomy to determine the position and the path of celestial objects. Astronomers use it to find the distance of the stars and planets from the Earth. Captain of a ship uses it to find the direction and the distance of islands and light houses from the sea. Surveyors use to map the new lands.
What is the objective of Chapter 8 in Class 10 Maths Trigonometry?
Objective of Class 10 Trigonometry:
Identifying the opposite side, adjacent side and hypotenuse of right triangle with respect to given angle A. Defining the six rations (sine, cosine, tangent, secant. cosecant and cotangent) related to the sides of a right angled triangle. Finding the values of trigonometric rations of a given right angled triangle. Finding the values of trigonometry rations of some standard angles (0, 30, 45, 60 and 90) in degrees. Using complementary angles and applying it into trigonometric identities to prove another identities.


