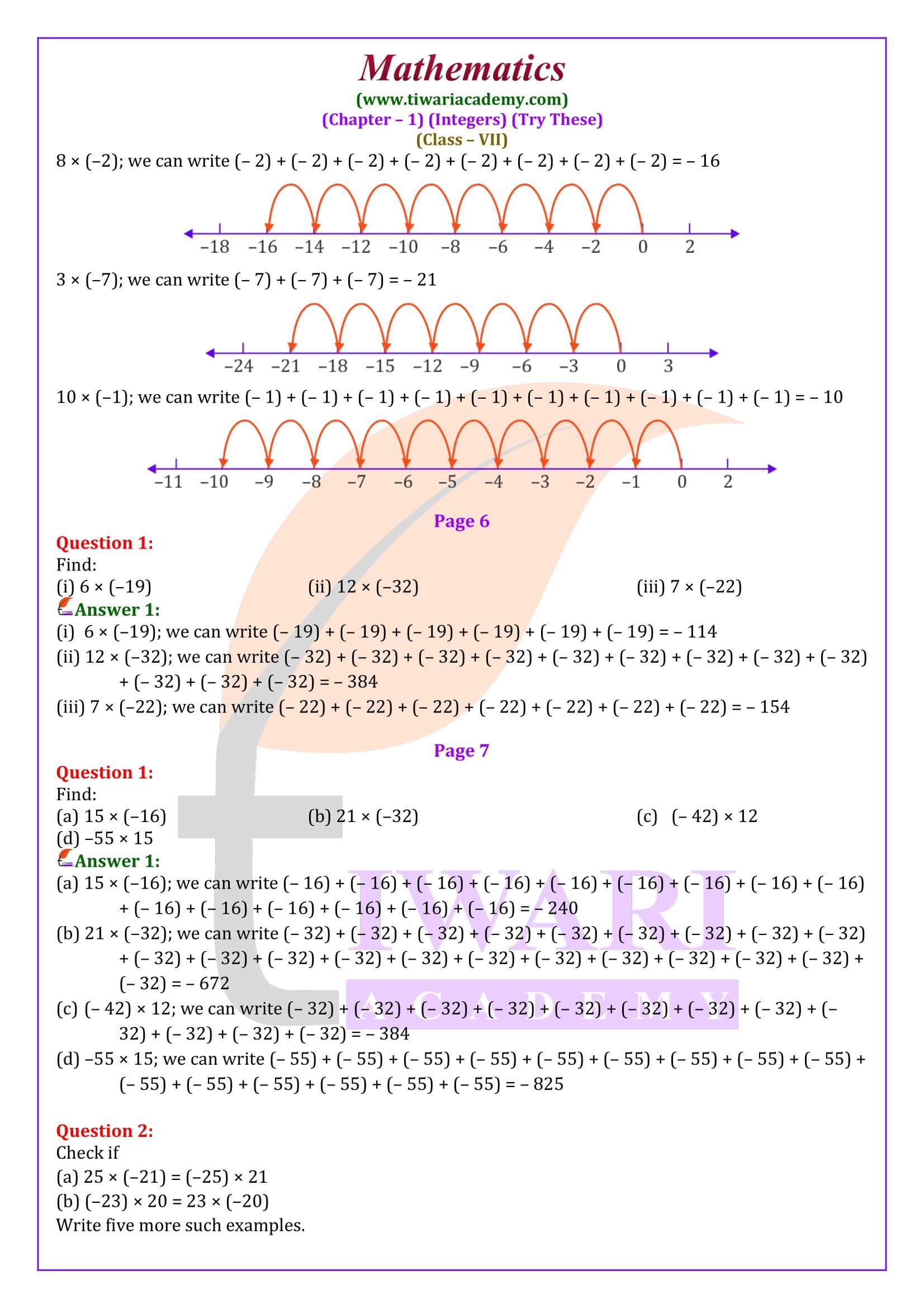
NCERT Solutions for Class 7 Maths Chapter 1 Integers and Class 7 Maths Chapter 1 Try These Solutions in Hindi and English Medium modified and updated for academic year 2024-25. According to new syllabus and latest textbooks for new session 2024-25, there are only three exercises in chapter 1 of class 7th mathematics.
Class 7 Maths Chapter 1 Solutions in English Medium
Practicing math concepts like integers from Class 7 can be very beneficial for understanding and mastering the topic. Here’s a step-by-step guide on how to effectively practice Class 7 Maths Chapter 1 Try These Integers. Preparing Class 7 Maths Chapter 1 (Integers) NCERT solutions involves a structured approach to understanding the concepts, solving problems, and creating clear explanations for students. Pay attention to definitions, examples, and the types of problems presented.
| Class: 7 | Mathematics |
| Chapter 1: | Integers |
| Number of Exercises: | 3 (Three) |
| Content: | NCERT Exercise Solutions |
| Mode: | Text, Images and Videos Format |
| Academic Session: | 2024-25 |
| Medium: | English and Hindi Medium |
Make sure you have a clear understanding of the basic concepts of integers, including positive and negative numbers, number line, absolute value, and addition/subtraction of integers. Integers are the central focus of this chapter. Make sure you have a clear understanding of what integers are, how they are represented on a number line, and their properties. Break down the chapter into key concepts and topics. These may include positive and negative integers, addition and subtraction of integers, and properties of integers. Read through the chapter in your textbook. Pay close attention to explanations, examples, and any solved problems.
Work through the practice exercises provided in the NCERT textbook. Solve the problems step by step to ensure you understand the process. Write down the step-by-step solutions for each type of problem. Make sure to explain each step clearly, addressing any potential difficulties students might face. Integers can be represented on a number line. Include diagrams and number lines to visually explain concepts, especially when discussing positive and negative integers.
Integers have real-life applications, like representing temperature, bank balances, and distances. Include relatable examples to help students connect the concept to their daily experiences. Anticipate common mistakes students might make and provide explanations to help them avoid these errors. Include a variety of problems, from basic to more complex, to challenge students’ understanding and problem-solving skills. Integers have certain rules for addition, subtraction, multiplication, and division. Note down these rules for quick reference.

NCERT Solutions for Class 7 Maths Chapter 1
7th Maths Exercise 1.1, Exercise 1.2 and Exercise 1.3 in English Medium and Prashnavali 1.1, Prashnavali 1.2 and Prashnavali 1.3 in Hindi Medium free to download in PDF format for new academic session. CBSE NCERT (https://ncert.nic.in/) Solution are given in simplified format. Videos related to each exercises are also given for better understanding. You can use NCERT solutions 2024-25 online or download in PDF file format without any login or password. Class 7 Maths solutions apps for online as well as offline use are also given free to download. Regular practice is key to mastering any math topic. Dedicate a specific amount of time each day for practicing integer-related problems. In videos, all the questions are described using proper properties of integers. The language of description is kept easy so that everyone can understand easily. For any inconvenience, contact us for help.
Review your solutions for accuracy, clarity, and coherence. Ensure your explanations are in line with the language and understanding of Class 7 students. Begin with easy problems and gradually move on to more complex ones. This will help you build confidence and progressively develop your skills. Format your solutions in a clear and organized manner. Use appropriate fonts, spacing, and headings to make the solutions easy to read. Proofread your solutions for any grammatical or typographical errors. Well-presented solutions enhance the learning experience.
If relevant, provide additional notes or tips for teachers and parents to assist them in explaining concepts effectively to students. Test your solutions with a few students or educators to get feedback. This helps ensure that your solutions are clear and understandable. Remember that the goal is to make Class 7 Maths Chapter 1 Integers NCERT solutions accessible, comprehensive, and engaging for students. Work through the example problems given in your textbook. These problems are designed to illustrate the concepts discussed in the chapter. The solutions should help students grasp the concepts, develop problem-solving skills, and build a strong foundation in mathematics.
7 Maths Chapter 1 Integers Solutions
NCERT Books for class 7 and CBSE Solutions 2024-25 for other subjects are also available for free download. We have prepared the Solutions in the simplified format so that students can understand easily. Look for additional practice worksheets, online resources, or apps that offer integer-related problems. Many educational websites and apps provide interactive quizzes and exercises. Invent your own integer problems based on real-life scenarios or mathematical concepts. Solving self-created problems can deepen your understanding of the subject. Class 7 Maths Chapter 1 solutions are given below in Hindi and English Medium.
Class 7 Maths Chapter 1 Important Questions
At Srinagar temperature was C on Monday and then it dropped by C on Tuesday. What was the temperature of Srinagar on Tuesday? On Wednesday, it rose by C. What was the temperature on this day?
On Monday, temperature at Srinagar = –5 oC
On Tuesday, temperature dropped = 2 oC
Temperature on Tuesday = –5 oC – 2 oC = –7 oC
On Wednesday, temperature rose up = 4oC
Temperature on Wednesday = –7 oC + 4 oC = –3 oC
Thus, temperature on Tuesday and Wednesday was –7 oC and –3 oC respectively.
A plane is flying at the height of 5000 m above the sea level. At a particular point, it is exactly above a submarine floating 1200 m below the sea level. What is the vertical distance between them?
Height of a place above the sea level = 5000 m
Floating a submarine below the sea level = 1200 m
The vertical distance between the plane and the submarine = 5000 + 1200 = 6200 m
Thus, the vertical distance between the plane and the submarine is 6200 m.
Mohan deposits ₹2,000 in his bank account and withdraws ₹1,642 from it, the next day. If withdrawal of amount from the account is represented by a negative integer, then how will you represent the amount deposited? Find the balance in Mohan’s accounts after the withdrawal?
Deposit amount = ₹2,000 and
Withdrawal amount = ₹1,642
Balance = 2,000 – 1,642 = ₹358
Thus, the balance in Mohan’s account after withdrawal is ₹ 358.
A certain freezing process requires that room temperature be lowered from 40 oC at the rate of 5 oC every hour. What will be the room temperature 10 hours after the process begins?
Given:
Present room temperature = 40 oC
Decreasing the temperature every hour = 5 oC
Room temperature after 10 hours = 40 oC + 10 x (–5 oC ) = 40 oC – 50 oC = – 10 oC
Thus, the room temperature after 10 hours is – 10 oC after the process begins.
A cement company earns a profit of ₹8 per bag of white cement sold and a loss of ₹ 5 per bag of grey cement sold. The company sells 3,000 bags of white cement and 5,000 bags of grey cement in a month. What is its profit or loss?
Given:
Profit of 1 bag of white cement = ₹ 8
And Loss of 1 bag of grey cement = ₹ 5
Profit on selling 3000 bags of white cement = 3000 x ₹ 8 = ₹ 24,000
Loss of selling 5000 bags of grey cement = 5000 x ₹ 5 = ₹ 25,000
Since Profit < Loss
Therefore, his total loss on selling the grey cement bags
= Loss – Profit
= ₹ 25,000 – ₹ 24,000 = ₹ 1,000
Thus, he has lost of `₹1,000 on selling the grey cement bags.
Practice problems involving addition, subtraction, multiplication, and division of integers. Try these word problems and puzzles that require application of integer concepts. Challenge yourself with more complex problems that require critical thinking and a deep understanding of the concepts. This will help you refine your problem-solving skills.

After solving problems, review your answers. Correcting mistakes is an important part of the learning process. If you’re facing difficulties, don’t hesitate to discuss the problems with your classmates, teacher, or parents. Sometimes, a different perspective can clarify things. Don’t overexert yourself. Take short breaks during your practice sessions to keep your mind fresh and focused.
About NCERT Solutions for Class 7 Maths Chapter 1
In 7 Mathematics Chapter 1 Integers, we will explore all the operations based on integer properties. Properties of integers on the operations like addition, subtraction, multiplication and division. Take mock tests or create a set of problems to test your understanding. Timed tests can help you practice solving problems under pressure. Schedule regular revision sessions to reinforce your understanding. Revise the concepts, rules, and formulas to keep them fresh in your mind. Remember, consistent practice and a positive attitude towards learning are key factors in succeeding in math. Don’t get discouraged by challenges; instead, view them as opportunities to improve. We have to learn about all the properties like closure, commutative, associative, etc. Integers are Closure under Addition but not under subtraction.
Class 7 Maths Chapter 1 Important Questions for Practice
1. When we divide a positive integer by a negative integer, we first divide them as whole numbers and then put a minus sign (–) before the quotient. That is, we get a negative integer.
2. The product of three integers does not depend upon the grouping of integers and this is called the associative property for multiplication of integers.
3. When we divide a negative integer by a positive integer, we divide them as whole numbers and then put a minus sign (–) before the quotient. We, thus, get a negative integer.
4. Addition is associative for integers, i.e., (a + b) + c = a + (b + c) for all integers a, b and c.
5. Integer 0 is the identity under addition. That is, a + 0 = 0 + a = a for every integer a.
Help and Support
We have prepared Hindi Medium NCERT Solutions for class 7 Maths on the demand of students. Now it is online on website to view online as well as for download. Time to time we modify our website on the basis of student’s suggestions. That is why Class 7 Maths App in English or Kaksha 7 Ganit App in Hindi Medium are developed for offline use.
How many exercises, questions, and examples are there in chapter 1 of class 7th Maths?
According to new syllabus and latest textbooks for session 2024-25, there are three exercises in chapter 1 (Integers) of class 7th Maths.
In the first exercise (Ex 1.1), there are 4 questions. Question 1 has three parts, question 2 has three parts, and question 4 has five parts.
In the second exercise (Ex 1.2), there are 9 questions. Question 2 has two parts, question 3 has two parts, and question 5 has eight parts.
In the third exercise (Ex 1.3), there are seven questions. Question 1 has nine parts, and question 2 has two parts.
So, there are in all 20 questions in chapter 1 (Integers) of class 7th Maths.
There is a total of 5 examples in chapter 1 (Integers) of class 7th Maths.
What will students study in chapter 1 of class 7th Maths?
In chapter 1 of class 7th Maths, students will study:
1. Properties of integers.
2. Addition and Subtraction of integers.
3. Statement Questions- Addition.
4. Multiplication of integers.
5. Distributive law in integers.
6. Statement Questions- Multiplication.
7. Division of Integers.
8. Statement Questions- Division.
Is chapter 1 of class 7th Maths difficult?
Chapter 1 of class 7th Maths is not easy and not difficult. It lies in the mid of easy and difficult because some parts of this chapter are easy, and some parts are difficult. But, the difficulty level of any chapter varies from child to child. So, Chapter 1 of class 7th Maths is easy or not depends on children also. Some children find it tough, some find it simple, and some find it in the middle of simple and tough.
How much time, students need to do chapter 1 of class 7th Maths?
Students need a maximum of 7-9 days to do chapter 1 of class 7th Maths if they give at least 1-2 hours per day to this chapter. This time is an approximate time. This time can vary because no students have the same working speed, same efficiency, same capability, etc.