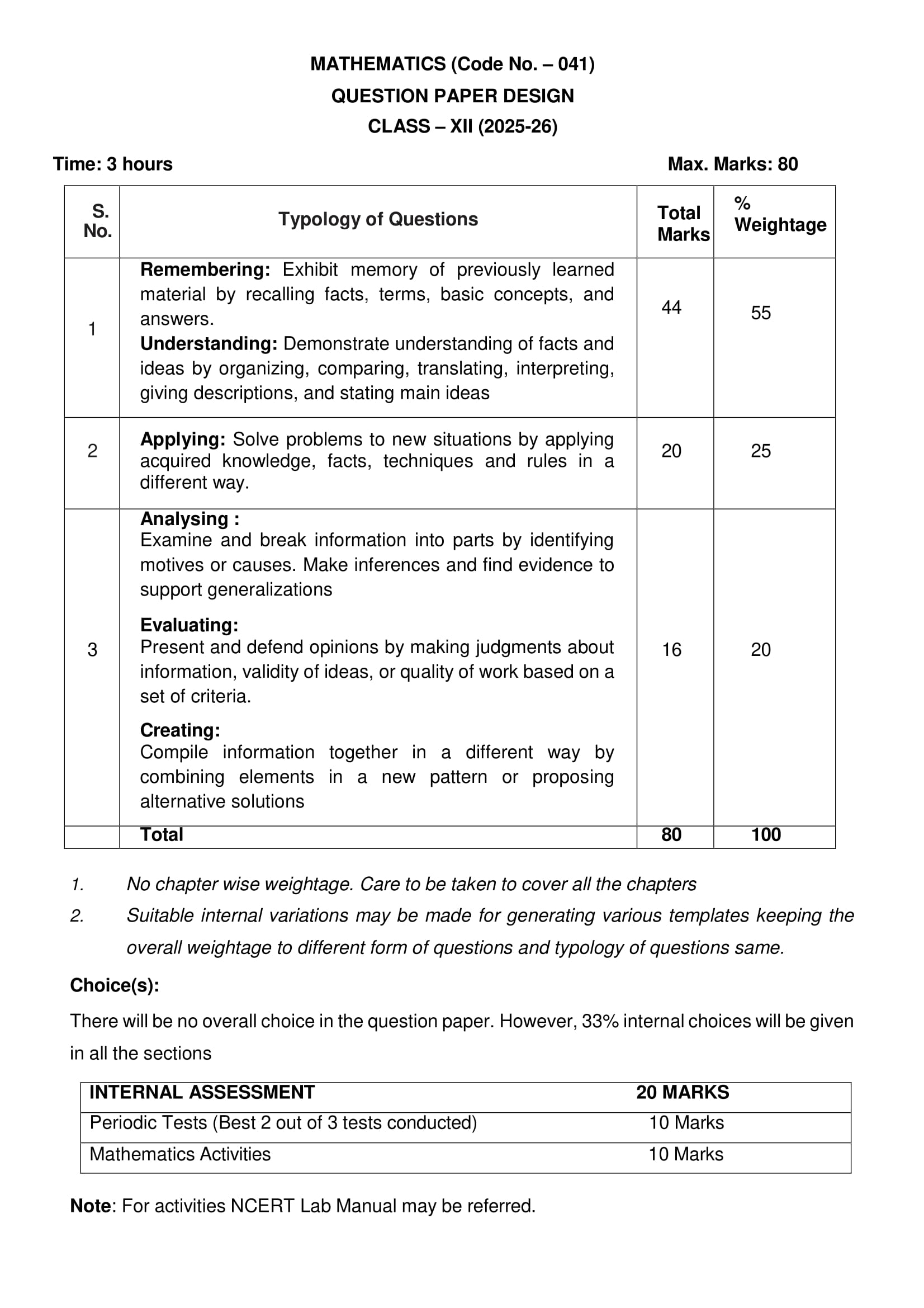
NCERT Chapter-wise Solutions for Class 12 Maths with MCQ based on the Mathematics Textbook PDFs in Hindi and English Medium for the CBSE Math Exam 2025-26. Class 12th Mathematics objective questions and NCERT Solutions are very important. They help students learn key concepts and techniques. These solutions cover many topics.
Some of them are Calculus, Matrices, Determinants, Vector Algebra, Probability and Linear Programming. The guide ensures a clear understanding of the subject. It is helpful for CBSE and other board exams. Students can use it to practice and prepare well.
Class 12 Maths NCERT Solutions for 2025-26 Exams
- Chapter 1. Relations and Functions
- Chapter 2. Inverse Trigonometric Functions
- Chapter 3. Matrices
- Chapter 4. Determinants
- Chapter 5. Continuity and Differentiability
- Chapter 6. Application of Derivatives
- Chapter 7. Integrals
- Chapter 8. Application of Integrals
- Chapter 9. Differential Equations
- Chapter 10. Vector Algebra
- Chapter 11. Three Dimensional Geometry
- Chapter 12. Linear Programming
- Chapter 13. Probability
Class 12 Maths MCQ Solutions with Explanation
Class 12 Math NCERT MCQ Solutions are very helpful. Maths Objective Question Answers support students in scoring well in board exams. Chapter-wise MCQs and solutions make learning easier. Students can understand tough topics like Inverse Trigonometry, Integration and Vectors. These solutions are often available as PDFs. Get here Class 12 Maths chapter-wise MCQ Solutions:
Chapter 1 MCQ (Relations and Functions)
Chapter 2 MCQ (Inverse Trigonometric Functions)
Chapter 3 MCQ (Matrices)
Chapter 4 MCQ (Determinants)
Chapter 5 MCQ (Continuity and Differentiability)
Chapter 6 MCQ (Application of Derivatives)
Chapter 7 MCQ (Integrals)
Chapter 8 MCQ (Application of Integrals)
Chapter 9 MCQ (Differential Equations)
Chapter 10 MCQ (Vector Algebra)
Chapter 11 MCQ (Three Dimensional Geometry)
Chapter 12 MCQ (Linear Programming)
Chapter 13 MCQ (Probability)
The content follows the CBSE Class 12 Math Syllabus. Previous year questions and sample papers with solutions boost exam preparation. Important topics like Matrices, Determinants and Vector Algebra are clearly explained. This helps students build strong concepts.
CBSE Syllabus Class 12 Maths for 2025-26
From Class 12 Mathematics Chapter 1 Functions and Relations to advanced topics like Integration, Differentiation, Vector Algebra and Probability, each chapter is systematically approached with analytical precision. The availability of Class 12th Math PDF Solution Downloads allows students to study offline, while Class 12 Math Complete Guide resources help them grasp key formulas, theorems and problem-solving strategies. With Extra Class 12 Maths Practice Papers and solved examples, students can enhance their skills, solidify their understanding and improve in CBSE Class 12 Mathematics and other board exam preparations with mathematical accuracy. Revised Study Plan and updated syllabus for Scoring well in board exams:
Study Plan for Class 12 Board Exam
Preparation of Class 12 Mathematics through Textbook Solutions, during the Exams
A well-structured study plan helps Class 12 students effectively cover Mathematics, balancing concepts, practice and revision. It ensures consistent learning, problem-solving and timely completion of chapters, building confidence for exams. By integrating Textbook Solutions, students gain clarity on concepts and master problem-solving techniques for better academic performance.
Success in class 12 mathematics isn’t about speed; it’s about persistence, understanding and never giving up.
| Time | Activity |
|---|---|
| 6:00 AM – 6:30 AM | Morning Exercise |
| 6:30 AM – 7:30 AM | Revision of Previous Topics |
| 7:30 AM – 8:30 AM | Practice Problems (Vectors/Calculus) |
| 8:30 AM – 9:00 AM | Breakfast & Relaxation |
| 10:00 AM – 12:00 PM | Focus on Core Concepts (3D, LPP, Probability) |
| 12:00 PM – 12:30 PM | Short Break |
| 12:30 PM – 1:30 PM | Problem-Solving (Past Year Papers) |
| 2:00 PM – 3:00 PM | Lunch & Relaxation |
| 3:00 PM – 4:30 PM | Advanced Practice (Integration/Differentiation) |
| 4:30 PM – 5:00 PM | Evening Break |
| 5:00 PM – 6:00 PM | Doubt Clearance & Revision |
| 6:00 PM – 7:00 PM | Mock Test |
| 7:30 PM – 8:00 PM | Dinner & Relaxation |
| 8:00 PM – 9:00 PM | Revision of the Day’s Work |
| 9:00 PM – 10:00 PM | Light Reading or Relaxation |
For those looking to deepen their understanding, the Class 12 Mathematics Chapter-wise Solutions provide targeted practice tailored to each topic. Key areas like Derivatives Solutions, Linear Programming Solutions and Continuity and Differentiability are explained with clarity, helping students master essential concepts. These solutions also align perfectly with the CBSE Class 12 Maths Syllabus, ensuring students focus on the most relevant topics for their exams. Resources like Class 12 Maths Important Questions and Class 12 Math Formulae enhance preparation, while comparison guides like Maths RD Sharma Comparison offer additional insights. Students can also access Class 12 NCERT Maths Solution Videos and Class 12th Math Online Solutions for interactive learning, making their preparation comprehensive and effective. Step-by-Step 12th Maths Solutions Guide for Every Chapter is prepared to meet the educational (NCERT) curriculum, empowering class 12 students to confidently tackle and understand the intricacies of school textbook and other Maths challenge.
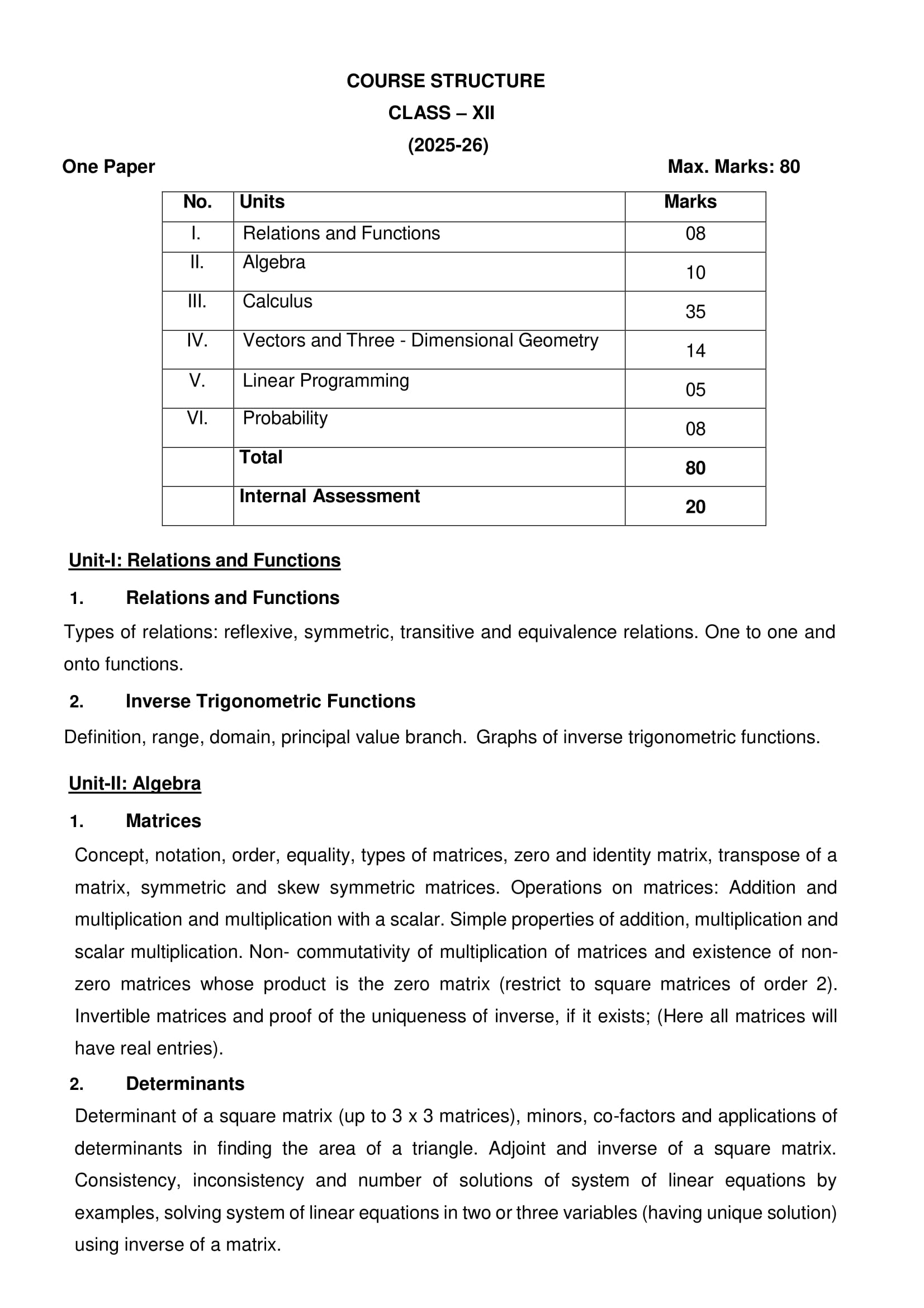
Chapter Wise Weightage of Class 12 Maths for 2025-26 Board Exams
| Chapters | Marks |
|---|---|
| 1. Relations and Functions, 2. Inverse Trigonometric Functions | 08 |
| 3. Matrices, 4. Determinants | 10 |
| 5. Continuity and Differentiability, 6. Application of Derivatives, 7. Integrals, 8. Application of Integrals, 9. Differential Equations | 35 |
| 10. Vector Algebra, 11. Three Dimensional Geometry | 14 |
| 12. Linear Programming | 05 |
| 13. Probability | 08 |
| Periodic Tests ( Best 2 out of 3 tests conducted) | 10 |
| Mathematics Activities | 10 |
| Total | 100 |
Simplify Class 12 Maths with Expertly Solved Solutions in India are valuable for students and teachers. Unlock Success with Class 12 Maths Solved Exercises and Study Materials are crucial as students prepare for important exams like the CBSE and various state board exams. Please provide your valuable Review and Feedback for further improvement. Class 12 Maths Explanations provide detailed and well-structured solutions to the problems and exercises in the course textbook of mathematics for class 12. This helps students prepare effectively for their CBSE board exams, as these exams follow the School curriculum 2025-26.
Class 12 Solutions Apps for iOS and Android
Chapter-Wise Textbook Solutions for Class 12 Maths: A Complete Guide, covers mathematical techniques and principles. These explained solutions guide help in building a solid Maths foundation, ensuring students score good marks in board exams, competitive tests and further academic pursuits.
It also includes examples that will help students better understand the concepts. The Tiwari Academy provides Class 12 Maths Solutions: Your Ultimate Study Resource which can be of great help to students.
Master Every Chapter with Class 12 Mathematics Solutions PDFs offer a variety of solved exercises and problems, perfect for practice and board exam revision. Question answers and Exercises solutions help students build problem-solving skills and confidence, especially in challenging topics like Calculus, including Differentiation and Integration. Regular practice with these solutions strengthens understanding and boosts exam readiness.
The Essence of Mathematics
Mathematics is a vast field that encompasses the study of numbers, formulas, structures, shapes, spaces and the changes in quantities. It is divided into major subdisciplines like number theory, algebra, geometry and analysis. Interestingly, there’s no universally accepted definition of mathematics among mathematicians, highlighting its diverse and evolving nature. When you encounter problems in the All You Need to Know About Class 12 Maths Solutions refer to the NCERT Textbook Solutions provided by Tiwari Academy. Follow these steps:
1. Read the solution carefully to understand how the formulae have been applied.
2. Attempt to solve the problem on your own first.
3. Compare your solution with the solution provided by Tiwari Academy.
4. Analyze any differences and learn from them. Carry on the process to master the subject.
NCERTNational Council of Educational Research and Training | Official Website: https://ncert.nic.in/ Easy-to-Follow Solutions for Class 12 Maths are indeed valuable resources for students preparing for their Class 12 Mathematics exams. Here’s why these solutions can be helpful for CBSE exams. Chapter-Wise Class 12 Maths PDFs for Hassle-Free Learning is designed to align with the curriculum prescribed by educational boards in India. This means they cover the topics and concepts that are essential for the Class 12 Mathematics exam.
Preparing for Class 12 Mathematics board exam becomes more effective with a structured approach, especially when incorporating Class 12 Math Exercises Solutions: The Perfect Board Exam Companion. Initially, it’s good to build a solid foundation in basic concepts. Make sure you have a clear understanding of the principles from previous grades, as Class 12 Maths is often an extension of those basic principles. Regular review and practice of these earlier concepts can greatly enhance your comprehension. Then, acquaint yourself with the Class 12 NCERT Mathematics Solutions to Help You Ace Your Exams with current syllabus. Identify the topics to be covered, focusing first on those that extend from your existing knowledge. This method eases the transition into more advanced topics. Use updated textbooks and other educational materials at Tiwari Academy, to gain a thorough understanding of each subject area. Solving a variety of problems is crucial for a better grasp of the subject and for preparation of board examination questions.
| Class: 12 | Mathematics Textbook |
| Number of Chapters: | 13 (Thirteen) |
| Content: | Class 12 Maths Guides |
| Content Type: | Images, Text, PDF and Video Format |
| Mode of Study: | Online and Offline Format |
| Academic Year: | Session 2025-26 |
| Medium: | Hindi and English Medium |
Many competitive exams in Bharat, such as engineering and medical entrance exams (e.g., JEE Main, NEET), require a strong foundation in mathematics. Class 12 mathematics solutions can be valuable for students preparing for these exams, as they cover essential topics and concepts commonly tested in such competitive exams.
Get Exam-Ready with Detailed Class 12 Maths Answers at Tiwari Academy are known for their clarity and accuracy. They provide step-by-step explanations for solving problems, making it easier for students to understand and follow the solutions. These solutions provide a wide range of practice problems and exercises. Practice is required for math exams, as it helps students become more comfortable with the concepts and improves problem-solving skills.
Teachers often use the Complete Guide to Class 12 Maths Problem Solving as teaching aids to explain concepts and solve problems in the classroom. These guides provide structured explanations and solutions that assist teachers in explaining the mathematical concepts effectively. NCERTNational Council of Educational Research and Training | Official Website: https://ncert.nic.in/ textbooks and solutions are widely recognized and accepted across India. They ensure a standardized curriculum and help maintain consistency in mathematics education across different states and regions. Solutions provided by Tiwari Academy are a valuable resource for teachers and students alike.
Key Points of 12th Maths Solutions
Accurate and Reliable Exercises Solution for Class 12 Maths Students, covers advanced mathematical concepts and topics suitable for students in their final year of secondary education. Here are some key points to consider about why solutions for Class 12 Maths Are Essential for CBSE Exams:
- The 12th Maths solutions cover a wide range of topics such as calculus, linear algebra, differential equations, Inverse Trigonometry, probability and vectors. These concepts are important for building a strong foundation in mathematics and preparing for higher studies.
- The explanations provide step-by-step explanations for various problems, helping students understand the logic and reasoning behind each step. This approach promotes better comprehension and problem-solving skills.
- The Maths solutions in grade 12th include a variety of problems, ranging from basic to complex. This allows students to gradually build their skills and tackle more challenging problems. These often provide real-world applications of mathematical concepts, helping students see the relevance of what they are learning.
- Class 12 Maths involves more abstract and analytical thinking. The solutions emphasize mathematical reasoning and logic, helping students develop a deeper understanding of the subject. These are designed to meet with the CBSE board exam pattern and guidelines. Practicing with these solutions can help students prepare effectively for their exams.
- Instead of just memorizing formulas, the solutions encourage students to understand the underlying concepts. This approach is crucial for mastering mathematics. Class 12 Maths involves graphical representations of functions and equations mainly in chapter 8 and 12. These help students interpret and draw various types of graphs accurately.
- The solutions of 12th Mathematics include a wide range of practice questions at the end of each chapter, allowing students to reinforce their learning and improve their problem-solving skills. These can be used as a valuable resource by teachers to explain the mathematical terms and principles and help them explain concepts effectively to their students. The official website and various educational platforms like Tiwari Academy offers Class 12 Maths NCERT solutions online, making them easily accessible for students.

Remember that Class 12 Maths can be difficult, but with consistent practice and a strong grasp of the concepts, you can have a good practice in the subject. It’s a good idea to use the Quick Access to Class 12 Maths Chapter-Wise Solutions in conjunction with extra study materials like past year papers. It is suggested that students seek guidance from teachers or tutors if needed.
Class 12 Maths Solutions Guide: Simplify Your Board Exam Preparation and focus on developing a deep understanding of the underlying mathematical concepts. This is essential for scoring well in exams, as questions may be designed to test your understanding rather than testing your memorizing ability. Since school textbooks and Free Class 12 Maths PDFs for Clear and Concise Learning are created to cater to the syllabus of the respective boards, they are highly relevant to the exams. Questions in the exams are often drawn from course textbooks and similar resources.
Expert-Solved Class 12 NCERT Math Solutions for Every Problem are valuable for all students and educators in India. They aid in exam preparation and build topic-wise clarity.
Class 12 Solutions App Download
Download Free PDFs of solutions for Class 12 Maths prepared by expert mathematicians and can help students understand the concepts better and score good marks in the exams. NCERT Solutions for Class 12 Maths in English and Hindi Medium have been updated for CBSE session. It provides a detailed explanation to promote a better conceptual understanding in students for all the topics included in CBSE Class 12 Maths Syllabus.
| Class 12 All Subjects iOS App for iPad & iPhone |
Users can easily update iOS and Android apps to access error-free solutions. This ensures that students always have access to the most accurate and up-to-date information. Using Tiwari Academy apps to Crack Class 12 Maths with Confidence Using Solutions reduces the need for physical textbooks, contributing to a more Eco-friendly learning environment.
Chapter-Wise Class 12 Maths Solutions with In-Depth Analysis include solutions to previous years CBSE board question, which can be extremely helpful for practice and understanding the exam pattern. In addition to the basic solutions, there are often additional exercises and problems provided in the NCERT textbooks and Class 12 Maths NCERT Solutions: A Student’s Step-by-Step Companion. These can be used to challenge yourself and further strengthen your skills.
Learn Class 12 Maths Concepts Faster with exercise solutions, designed by our Expert Maths teachers to facilitate smooth and clear understanding of concepts and logic. These solution covers all the formulae and theorems with step by step method so that student can easily understand. You can get all chapter wise all exercise solutions for the Class 12 Maths Books.
It’s important to note that while the Ultimate Guide to Class 12 Maths Solved Questions are a valuable resource, they may not cover every possible type of question or provide extensive practice for highly competitive exams. Depending on your goals and the level of your preparation, you may also want to explore other textbooks, reference books, online resources and practice past years papers.
Class 12 Maths NCERT Detailed Solutions, Trusted Resource for CBSE Students, are an excellent starting point for your exam preparation, but it is advisable to supplement your study with a variety of resources to ensure easy preparation for your Class 12 Mathematics exam.
You can download NCERT Class 12 Maths Solutions App for all exercises by just clicking these links here. Using Class 12 Maths Solutions for Better Exam Scores play a lead role in supporting students’ learning and understanding of complex mathematical concepts. It covers advanced topics like calculus, verctor-3D and probability, which can be challenging to grasp. At Tiwari Academy, the solutions for Class 12 Mathematics: Perfect for Exam Prep, provide clear explanations, breaking down complex concepts in a way that can be more absorbing. They also help students in understanding the underlying principles.
Board exams are a significant milestone. NCERT Solutions for Class 12 Mathematics: Chapter-Wise PDFs for Free, align with the CBSE curriculum 2025-26, providing practice questions similar to those that might appear in the exams. This helps students prepare effectively and boosts their performance.
In the next phase, concentrate on problem-solving and practical application, utilizing Complete Solutions for Class 12 Mathematics with Expert Guidance. Engage in consistent practice with different problem types, including exercises from textbooks, previous exam papers and additional questions from various math workbooks or online platforms. If you face challenges, seek assistance from teachers, tutors or educational resources like videos and online forums. It is also important to understand the theories underlying mathematical concepts, as this can make problem-solving more intuitive. Managing your time and stress effectively is needed. Develop a study plan that includes regular mathematics practice, using Step-by-Step Solutions for Class 12 Mathematics Problems, while also balancing time for other subjects and activities. Remember, consistent study is more beneficial than last-minute cramming for exams.
Class 12 Maths Syllabus Revised for 2025-26
Ace Your Exams with NCERT Solutions for Class 12 Mathematics
Your Ultimate Guide to solutions for Class 12 Mathematics includes advanced topics like calculus, matrices and determinants, differential equations, probability and vectors. Math textbook solutions help students understand these concepts clearly and guide them through solving different types of problems.
It’s important to note that Chapter-Wise solutions for Class 12 Mathematics Explained not only meant for providing answers but also for enhancing understanding and building problem-solving skills. They serve as a valuable resource for students, helping them master the concepts and improve in their studies.
Class 12 Maths Chapter 1 Relations and Functions Solutions
Class 12 Maths, Relations and Functions is the first chapter of the Class 12 Maths Book. There are 3 exercises in this Solution for class 12 Maths Chapter 1.
Class 12 Maths Exercise 1.1
Class 12 Maths Exercise 1.2
Class 12 Maths Miscellaneous 1
Class 12 Maths Exercise 1.1 in Hindi
Class 12 Maths Exercise 1.2 in Hindi
Class 12 Maths Miscellaneous 1 in Hindi
Chapter 1 Relations and Functions in NCERT Class 12 Maths, covers topics like types of relations, functions, composition, domains, co-domains, composite functions and invertible functions. Tiwari Academy’s NCERT textbook explanation, crafted by expert Mathematics teachers, provide in-depth explanations in both Hindi and English.
NCERT Class 12 Maths Chapter 2 Inverse Trigonometric Functions Guide
NCERT Solutions for Class 12 Maths Chapter 2 Inverse Trigonometric Functions covers various topics such as concepts of inverse trigonometric functions, inverse trigonometric functions properties, and miscellaneous examples.
Class 12 Maths Exercise 2.1
Class 12 Maths Exercise 2.2
Class 12 Maths Miscellaneous 2
Class 12 Maths Exercise 2.1 in Hindi
Class 12 Maths Exercise 2.2 in Hindi
Class 12 Maths Miscellaneous 2 in Hindi
Chapter 2 of NCERT Class 12 Maths includes two exercises that explain the range of trigonometric functions and their behavior in graphs. Study materials for mathematics and well-structured NCERT textbook solutions, prepared by experienced teachers, make learning easy and clear.
NCERT Detailed Solutions for Class 12 Maths Chapter 3 Matrices
NCERT Solutions for Class 12 Maths Chapter 3 Matrices you can understand the definition of Matrices, various types of matrices, equality of matrices, operations on matrices such as the addition of matrices and multiplication of matrices by a scalar.
Class 12 Maths Exercise 3.1
Class 12 Maths Exercise 3.2
Class 12 Maths Exercise 3.3
Class 12 Maths Exercise 3.4
Class 12 Maths Miscellaneous 3
Class 12 Maths Exercise 3.1 in Hindi
Class 12 Maths Exercise 3.2 in Hindi
Class 12 Maths Exercise 3.3 in Hindi
Class 12 Maths Exercise 3.4 in Hindi
Class 12 Maths Miscellaneous 3 in Hindi
In this NCERT Mathematics section, you’ll learn about matrix addition, scalar multiplication, matrix multiplication, and properties of each. Topics also include transpose of matrices, symmetric and skew-symmetric matrices, elementary transformations and finding inverses using elementary operations, along with miscellaneous examples. Class 12 Maths textbook solutions for Matrices are available in Hindi and English, in both text and video formats.
NCERT Exercise Solutions Class 12 Maths Chapter 4 Determinants
NCERT Solutions for Class 12 Maths Chapter 4 Determinants covers all topic of determinants. You can learn and study here about the definition and meaning of determinants.
Class 12 Maths Exercise 4.1
Class 12 Maths Exercise 4.2
Class 12 Maths Exercise 4.3
Class 12 Maths Exercise 4.4
Class 12 Maths Exercise 4.5
Class 12 Maths Miscellaneous 4
Class 12 Maths Exercise 4.1 in Hindi
Class 12 Maths Exercise 4.2 in Hindi
Class 12 Maths Exercise 4.3 in Hindi
Class 12 Maths Exercise 4.4 in Hindi
Class 12 Maths Exercise 4.5 in Hindi
Class 12 Maths Miscellaneous 4 in Hindi
NCERT Class 12 Maths chapter 4 includes six exercises covering topics like the order and properties of determinants, calculating the area of a triangle with determinants, finding minors, adjoints and co-factors and solving systems of linear equations (in two and three variables) using matrix inverses.
Class 12 NCERT Math Solutions Chapter 5 Continuity and Differentiability
Class 12 Maths Chapter 5 Continuity and Differentiability textbook has eight exercises which are based on 12th Class Maths Book Solution, in the 1st exercise you just learn about the definition of continuity.
Class 12 Maths Exercise 5.1
Class 12 Maths Exercise 5.2
Class 12 Maths Exercise 5.3
Class 12 Maths Exercise 5.4
Class 12 Maths Exercise 5.5
Class 12 Maths Exercise 5.6
Class 12 Maths Exercise 5.7
Class 12 Maths Miscellaneous 5
Class 12 Maths Exercise 5.1 in Hindi
Class 12 Maths Exercise 5.2 in Hindi
Class 12 Maths Exercise 5.3 in Hindi
Class 12 Maths Exercise 5.4 in Hindi
Class 12 Maths Exercise 5.5 in Hindi
Class 12 Maths Exercise 5.6 in Hindi
Class 12 Maths Exercise 5.7 in Hindi
Class 12 Maths Miscellaneous 5 in Hindi
Next, you’ll study continuity, the algebra of continuous functions, differentiability, derivatives of implicit and composite functions and derivatives of inverse trigonometric functions. Topics also include logarithmic differentiation, exponential and logarithmic functions, parametric derivatives, second-order derivatives and the mean value theorem, with various examples for board exam practice.
Class 12 Mathematics Solutions Chapter 6 Applications of Derivatives
Exercise Solutions for Class 12 Maths Chapter 6 Applications of Derivatives has five exercises which cover the definition of derivatives, tangents normal, rate of change of quantities, increasing and decreasing functions.
Class 12 Maths Exercise 6.1
Class 12 Maths Exercise 6.2
Class 12 Maths Exercise 6.3
Class 12 Maths Miscellaneous 6
Class 12 Maths Exercise 6.1 in Hindi
Class 12 Maths Exercise 6.2 in Hindi
Class 12 Maths Exercise 6.3 in Hindi
Class 12 Maths Miscellaneous 6 in Hindi
NCERT 12 Mathematics Chapter 6 covers the applications of derivatives, including approximation, finding maxima and minima, the first derivative test, functions in a closed interval and miscellaneous examples. NCERT textbook solution for Class 12 Maths provide detailed explanations, available in both Hindi and English, to suit student needs.
Class 12 Maths Chapter 7 Integrals NCERT Exercise Solutions
Class 12 Maths Chapter 7 Integration has twelve exercises which cover the definition of integration, definite and indefinite integrations and limit of sums based questions.
Class 12 Maths Exercise 7.1
Class 12 Maths Exercise 7.2
Class 12 Maths Exercise 7.3
Class 12 Maths Exercise 7.4
Class 12 Maths Exercise 7.5
Class 12 Maths Exercise 7.6
Class 12 Maths Exercise 7.7
Class 12 Maths Exercise 7.8
Class 12 Maths Exercise 7.9
Class 12 Maths Exercise 7.10
Class 12 Maths Miscellaneous 7
Class 12 Maths Chapter 7 in Hindi Medium
Class 12 Maths Exercise 7.1 in Hindi
Class 12 Maths Exercise 7.2 in Hindi
Class 12 Maths Exercise 7.3 in Hindi
Class 12 Maths Exercise 7.4 in Hindi
Class 12 Maths Exercise 7.5 in Hindi
Class 12 Maths Exercise 7.6 in Hindi
Class 12 Maths Exercise 7.7 in Hindi
Class 12 Maths Exercise 7.8 in Hindi
Class 12 Maths Exercise 7.9 in Hindi
Class 12 Maths Exercise 7.10 in Hindi
Class 12 Maths Miscellaneous 7 in Hindi
NCERT Class 12 Math Solutions Chapter 8 Applications of Integrals
In Textbook Solutions for Class 12 Maths Chapter 8 Applications of Integrals, students can get an overall knowledge about the area bounded and specific application of integrals.
Class 12 Maths Exercise 8.1
Class 12 Maths Miscellaneous 8
Class 12 Maths Exercise 8.1 in Hindi
Class 12 Maths Miscellaneous 8 in Hindi
It covers the definition of Integrals, especially lines, circles/ parabolas/ellipses, area under simple curves, area between two curves and at last miscellaneous examples. There are two exercises in NCERT Solutions for Class 12 Maths Chapter 8. We have prepared the solutions based on 12th Class Maths NCERT Book part 2. Solutions to area bounded Class 12 Maths are available in Hindi and English medium.
NCERT Complete Solutions Class 12 Maths Chapter 9 Differential Equations
Students can understand the definition of Differential Equations in the solutions for Class 12 Maths Chapter 9 Differential Equations.
Class 12 Maths Exercise 9.1
Class 12 Maths Exercise 9.2
Class 12 Maths Exercise 9.3
Class 12 Maths Exercise 9.4
Class 12 Maths Exercise 9.5
Class 12 Maths Miscellaneous 9
Class 12 Maths Exercise 9.1 in Hindi
Class 12 Maths Exercise 9.2 in Hindi
Class 12 Maths Exercise 9.3 in Hindi
Class 12 Maths Exercise 9.4 in Hindi
Class 12 Maths Exercise 9.5 in Hindi
Class 12 Maths Miscellaneous 9 in Hindi
It clears basic concepts related to differential equations and many more with step by step solutions so that students can easily understand. It covers all the solutions based on 12th Class Maths Book Solution including the degree of a differential equation, order of a differential equation, general and particular solutions of a differential equation, homogeneous differential equations, linear differential equations, procedure involved formation of a differential equation etc. Students can take help for Differential Equations of 12th standard in Hindi and English medium.
Solutions Guide for Class 12 Maths Chapter 10 Vector Algebra
Solution Guides for Class 12 Maths Chapter 10 Vector Algebra, can help the students to understand about the introduction of vector algebra, position vector and some basic concepts related to vector algebra.
Class 12 Maths Exercise 10.1
Class 12 Maths Exercise 10.2
Class 12 Maths Exercise 10.3
Class 12 Maths Exercise 10.4
Class 12 Maths Miscellaneous 10
Class 12 Maths Exercise 10.1 in Hindi
Class 12 Maths Exercise 10.2 in Hindi
Class 12 Maths Exercise 10.3 in Hindi
Class 12 Maths Exercise 10.4 in Hindi
Class 12 Maths Miscellaneous 10 in Hindi
In Class 12 Maths Chapter 10, you’ll explore algebraic and geometric properties, vector multiplication by a scalar, vector joining two points, vector components, section formula and vector products. 12th Maths chapter 10 includes four exercises plus a miscellaneous section. Find complete, step-by-step solutions based on the Class 12 Maths book, available in both Hindi and English.

NCERT Exercises Solutions for Class 12 Maths Chapter 11 Three Dimensional Geometry
Textbook Solutions for Class 12 Maths Chapter 11 Three Dimensional Geometry, you can get know about Three Dimensional Geometry. The student can master topics on three dimensional geometry, direction cosines and direction ratios.
Class 12 Maths Exercise 11.1
Class 12 Maths Exercise 11.2
Class 12 Maths Miscellaneous 11
Class 12 Maths Exercise 11.1 in Hindi
Class 12 Maths Exercise 11.2 in Hindi
Class 12 Maths Miscellaneous 11 in Hindi
Learn the properties of line, equation of a line through a given point and parallel direction cosines of a line passing through two points, relation between the direction cosines of a line, equation of a line in space, plane passing through the intersection of two given planes, angle between two planes, co-planarity of two lines and many more. There are three exercises and a miscellaneous exercise in chapter 11 of 12th Mathematics NCERT.
Class 12 Maths Chapter 12 Linear Programming NCERT Solutions
You are introduced to Solutions for Class 12 Maths Chapter 12 Linear Programming. Here this chapter covers linear programming problem and its mathematical formulation.
Class 12 Maths Exercise 12.1 in Hindi
You will learn about the mathematical formulation of the problem, different types of all linear programming problems graphical feasible and infeasible method solution. NCERT Solutions for Class 12 Maths Chapter 12 covers two exercises in all. Solutions to the Linear Programming Problems of 12th Mathematics are available in Hindi and English medium both.
NCERT Class 12 Mathematics Chapter 13 Probability Solutions
In this last chapter of Solutions for Class 12 Maths Chapter 13 Probability, you will learn what is probability and Multiplication rule of the same.
Class 12 Maths Exercise 13.1
Class 12 Maths Exercise 13.2
Class 12 Maths Exercise 13.3
Class 12 Maths Miscellaneous 13
Class 12 Maths Exercise 13.1 in Hindi
Class 12 Maths Exercise 13.2 in Hindi
Class 12 Maths Exercise 13.3 in Hindi
Class 12 Maths Miscellaneous 13 in Hindi
You can understand here the concept of random variables and its probability in this chapter. Other than this chapter also covers mean of random variable, variance of random variable and binomial distribution and Bernoulli trials with miscellaneous examples. NCERT Solutions for Class 12 Maths Chapter 13 describes about the five topics with well-defined solutions by the expert math teachers.
Importance of Learning Solutions for Class 12 Maths from Tiwari Academy
Students can get the following benefits if they learn and practice from Tiwari Academy App/website for class 12 Mathematics:
1. Clears your doubt easily through simple explanation.
2. Provides best study material for the preparation of academic and competitive exams.
3. Helps you to build a strong base for higher classes.
There are a total of 13 chapters-solutions for which are given by experienced mathematics teachers reviewed too. By learning properly and practice this Class 12 Mathematics Made Easy with Solutions, will enable you to score well in class 12th board exams.
Provides Authentic Information to the Students
Download Free Textbook Solutions for Class 12 Mathematics now provided by the experienced Maths teachers after extensive research on each and every chapter to provide correct and authentic information to the students.
Follows the CBSE Curriculum
This is yet another most important reason why you should follow Exercises Solutions given by us. These for every chapter strictly adhere to the CBSE curriculum 2025-26.
Clears all Fundamental Logic & Concepts
These NCERT solutions help the students to make their concepts crystal clear. Once you clear the concept then there is no need to read the whole chapter again and again.
Helpful For Revisions during Examinations
Master Class 12 Mathematics with complete NCERT Solutions which are designed in such a way that Students can revise quickly during their Examinations.
CBSE 12 Maths MCQ Solutions Helpful for Board Exams
Class 12 Maths NCERT MCQ Solutions: Free Chapter-wise MCQ PDF Downloads – help you to secure good marks in the 12th class Board exams since they make your concepts crystal clear.
By practicing and revising MCQ Chapter-wise Solutions for Class 12 Mathematics – All Chapters Solved given by us, there is probability of scoring above 90 percent marks in the board examination. In the past, students have scored high marks in mathematics class 12th by following and learning from our website and apps.
Complete Detailed Solutions for Class 12 Maths: A Step-by-Step Guide is a valuable tool for self-study, allowing students to review topics at their own pace and strengthen their understanding. They serve as a reference for checking answers in homework and practice exercises, helping students spot and correct mistakes. Class 12 Maths NCERT Simple Solutions for CBSE Board Exam Preparation, emphasize understanding the logic behind mathematical techniques, not just memorizing formulas, which improves comprehension and critical thinking skills.

How to get class 12 Maths NCERT Solutions?
Get the revised and modified Expert-Solved NCERT Solutions for Class 12 Maths Problems to prepare for board exams. As you know the syllabus is reduced for academic year 2025-26. So, follow the instruction to get appropriate NCERT textbook solution for final exams. If you still have doubts or questions, don’t hesitate to ask your teacher or a peer for clarification. Clearing up any confusion is essential to build a strong foundation in mathematics. Follow the steps given here to get Chapter-Wise NCERT Solutions for Class 12 Maths with Explanations in Hindi and English Medium.
- Step 1: Search the website for class 12 Maths NCERT Solutions.
- Step 2: Visit to Class 12 Maths solutions based Educational Websites like Tiwari Academy.
- Step 3: Use Class 12 Maths Solutions App to get Hindi and English medium content.
- Step 4: Prepare Class 12 Maths for board exams using NCERT Solutions.
- Step 5: Crosscheck the answers and Solution using NCERT Solutions of Class 12 Maths.
Step 1: Search the website for class 12 Maths NCERT Solutions.

Step 2: Visit to Class 12 Maths solutions based Educational Websites like Tiwari Academy.

Step 3: Use Class 12 Maths Solutions App to get Hindi and English medium content.

Step 4: Prepare Class 12 Maths for board exams using NCERT Solutions.

Step 5: Crosscheck the answers and Solution using NCERT Solutions of Class 12 Maths.

Your Ultimate Guide to NCERT Textbook Solutions for Class 12 Maths textbook part 1 and part 2 are available in various formats, including books, online platforms and mobile apps. This accessibility ensures that students can choose the format that suits their learning preferences. Free Class 12 Maths Exercises Solutions: Simplified for Students – provide clarity, guidance and practice for students facing intricate mathematical challenges.
For students seeking targeted assistance, Class 12 Math Important Questions with Solutions focus on scoring topics like Probability Chapter Solutions, Linear Programming and Differential Equations. A handy Class 12 Maths Formula further simplifies problem-solving by consolidating essential formulas in one place. Interactive tools such as Class 12 Math Online Solutions and Class 12 Mathematics Solution Videos offer dynamic learning experiences, making complex concepts easier to grasp. By utilizing Class 12 Math Study Material, students can strengthen their command over topics like 3D Geometry and tackle both theory and application-based problems effectively. These comprehensive resources empower students to confidently approach their exams and achieve outstanding results.
Is NCERT Enough for Class 12 Maths Board Exams?
Yes, NCERT Class 12 Maths Books are enough to score maximum marks in the Class 12 Board exams. Just practice all the exercise and learn the theorems. Also, do not skip any topic of CBSE 12th Maths syllabus and revise 2-3 times before your class 12 board exam. The NCERT books for Class 12 are prescribed by the CBSE itself. So these NCERT books are known for their clear explanation of each topic and a good level of practice questions. It is the best study material for Class 12 Boards Maths. These NCERT textbooks are enough for you to score well in your CBSE Class 12 Maths board exam.
Which Book is Best for Class 12 Maths Board Exam?
NCERT Book is the best and most trusted book for Class 12 board exam. Students can clear their concepts and logics through NCERT Class 12 Maths book by solving the examples and all exercise problems. Students are advised to solve questions from the NCERT book as this book follows the pattern prescribed by CBSE.
Is Class 12 Maths Difficult?
For students who have understood the concepts of class 11, there no need to worry about the class 12th mathematics. By sufficient practice of questions, students can score good marks in board exams. In case of any doubt, students can refer to solutions provided by Tiwari Academy and understand the concepts behind the solutions.
Which website is best for Class 12 maths NCERT solutions?
You can find many websites online which are providing Maths NCERT solutions for class 12. But tiwariacademy.com provides a solid conceptual base for all the topics included in CBSE Class 12 Maths Syllabus. All solutions cover all the important theorems and formulae with detailed explanations so that student can easily clear the concept.
Tiwari Academy is one of the best websites because of the following reasons:
1. A detailed step-by-step explanations of problems is given for NCERT textbooks questions.
2. Apart from solutions, the best study materials for students who are preparing for their Class 12 board exams is given.
3. From this website, you can get FREE Class 12 Maths NCERT solutions in PDF formats.