Chapter Wise Class 10 Maths NCERT Solutions
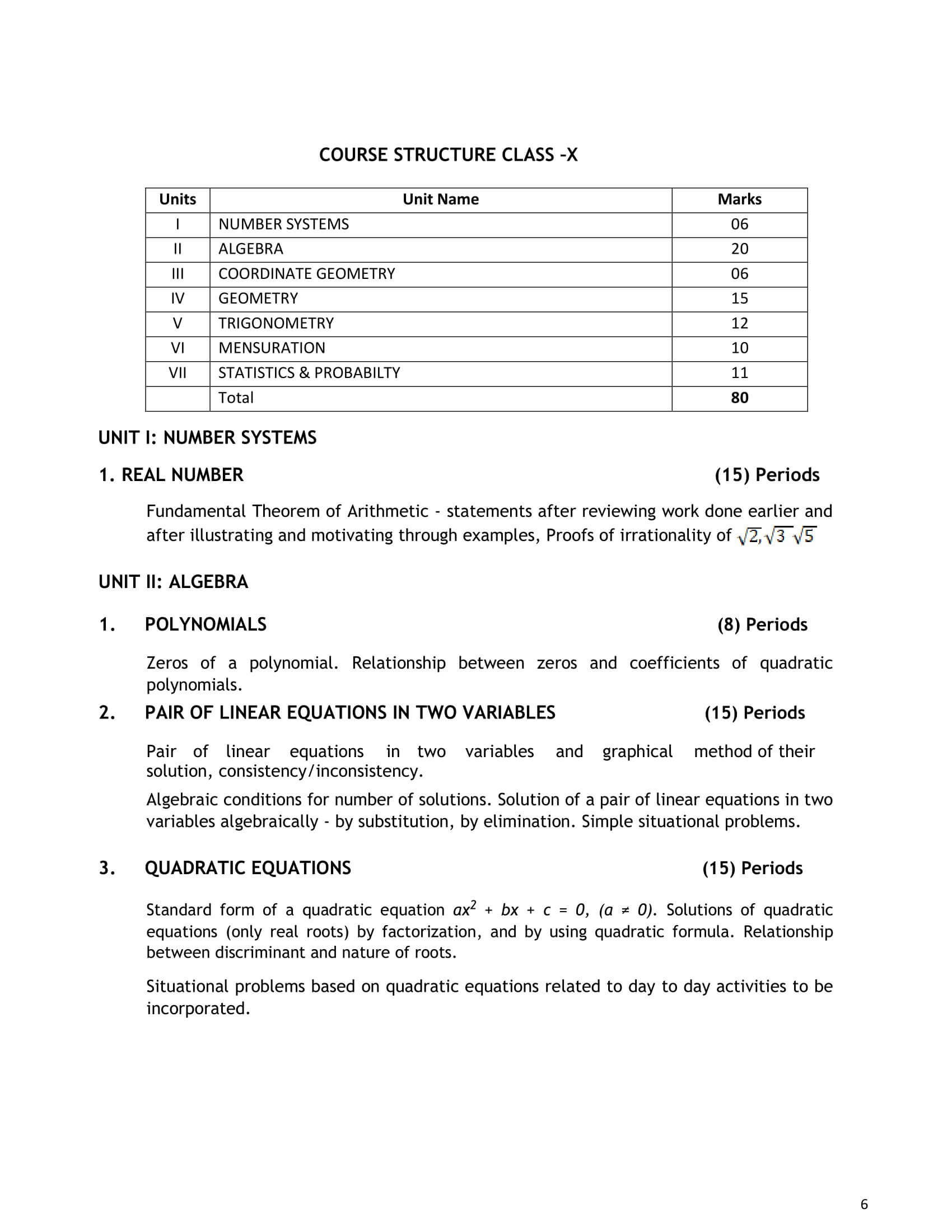
CBSE Syllabus Class 10 Maths for 2024-25
Chapter 1. Real Numbers
Chapter 2. Polynomials
Chapter 3. Pair of Linear Equations
Chapter 4. Quadratic Equations
Chapter 5. Arithmetic Progression
Chapter 6. Triangles
Chapter 7. Coordinate Geometry
Chapter 8. Introduction to Trigonometry
Chapter 9. Applications of Trigonometry
Chapter 10. Circles
Chapter 11. Area Related to Circles
Chapter 12. Surface Areas and Volumes
Chapter 13. Statistics
Chapter 14. Probability
NCERT Solutions of Class 10 Maths
NCERT Solutions for Class 10 Maths in Hindi and English Medium updated for session 2024-25 CBSE and State boards. At Tiwari Academy, we provide NCERT Solutions in PDF and Videos format specifically designed for Class 10 Maths based on new syllabus.
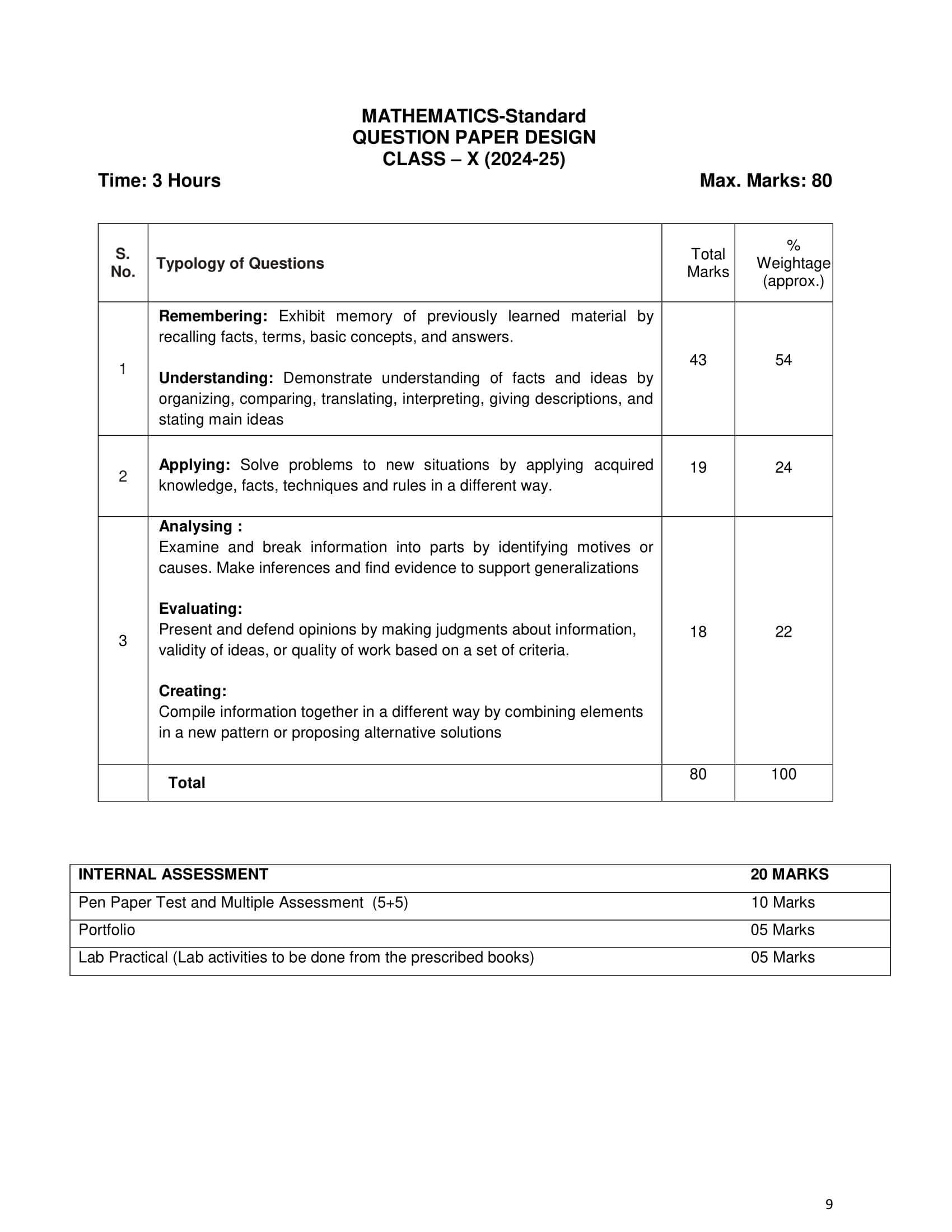
Weightage of Chapters: Class 10 Maths Session 2024-25
| Chapters | Weightage |
|---|---|
| 1. Real Numbers | 06 |
| 2. Polynomials, 3. Pair of Linear Equations, 4. Quadratic Equations, 5. Arithmetic Progression | 20 |
| 7. Coordinate Geometry | 06 |
| 6. Triangles, 10. Circles | 15 |
| 8. Introduction to Trigonometry, 9. Applications of Trigonometry | 12 |
| 11. Area Related to Circles, 12. Surface Areas and Volumes | 10 |
| 13. Statistics, 14. Probability | 11 |
| Pen Paper Test and Multiple Assessment | 10 |
| Portfolio | 05 |
| Lab Practical (Lab activities to be done from the prescribed books) | 05 |
| Total | 100 |
Check here the complete description of Class 10 Maths Syllabus for 2024-25. Class 10 Maths solution guides are available in both Hindi and English Medium. Check the accuracy and completeness of NCERT solutions and Rate and Review with your feedback.
Class 10 Solutions Apps Download
NCERT solutions are widely used by students and teachers alike because they are designed by experts and follow the curriculum prescribed by the central educational board. Oswaal CBSE Question Banks Class 10 2024-25 for 2024 Board Exam | Trusted by 3 Lakh Teachers, 50000 Schools, and 13M Parents. They provide step-by-step explanations for various mathematical concepts, formulas, and problem-solving techniques.
To get good marks student need more practice preparing for a class 10 Maths exam. Regular practice helps reinforce the mathematical concepts you’ve learned in class 10. 10th Maths Syllabus revised for 2024-25, involves solving problems, and the more you practice, the better you become at solving different types of problems. Tiwari Academy offers supplementary materials like practice questions, video explanations, and sample papers to help students better prepare for exams.
You can find the revised and modified Class 10 Maths NCERT solutions based non new curriculum for 2024-25. Using these solutions can enhance your understanding of the subject and improve your problem-solving skills. Oswaal CBSE Sample Papers Class 10 2024-25 for 2025 Board Exam | Trusted by 3 Lakh Teachers, 50000 Schools, and 13 M Parents.
Class 10 Mathematics Syllabus for 2024-25

| Class: 10 | Mathematics |
| Number of Chapters: | 14 (Fourteen) |
| Contents: | NCERT Exercises, Extra Questions, Test Papers |
| Content Type: | Text, Videos, Images and PDF Format |
| Academic Year: | 2024-25 |
| Medium: | English and Hindi Medium |
Class 10 Solution Apps
Solutions of all exercises from Chapters 1 to 14 and textbooks from NCERT website are available in PDF at Tiwari Academy. The NCERT textbook solutions are prepared by experts and will help you understand the concepts better and score high in your exams.
It’s also a good idea to explore multiple resources of Class 10 Maths Solutions and choose the one that aligns best with your learning style and needs. You can also consult with your teachers for recommendations on reliable resources for Class 10 Maths NCERT solutions.
The amount of daily practice needed for Class 10 Maths may vary from person to person. Some students need more practice than others to feel confident in their math skills.
Get the Class 10 Maths solution solved through various methods. You can visit the website and navigate to the E-Books section to find the Class 10 Maths textbook and its solutions. If you already have a good understanding of the basic concepts, you need less time to cover the syllabus. Some students of 10th Maths grasp mathematical concepts more quickly than others, which can affect the time needed to complete the syllabus.
There are numerous educational websites and platforms like Tiwari Academy that offer free NCERT solutions for Class 10 Maths for Session 2024-25. Compare the cost of using Tiwari Academy with other similar resources. Our website offers free Class 10 Maths NCERT solutions, while others charge a fee. There are mobile apps available for both Android and iOS devices that provide NCERT solutions.
NCERT Solutions for Class 10 Maths All Chapters at new pattern
Find NCERT Solutions for Class 10 Maths App all Chapters, which are provided by the expert math teacher. Class 10 Maths Solutions are revised and updated topic wise for session 2024-25 both Hindi and English medium.
NCERT Class 10 Maths all Chapter’s Solution
As per the revised NCERT book for 10th Maths released for 2024-25, there are 14 chapters in all, and here you can get solutions for all chapters provided by the skilled Maths subject teacher. Math is one of the most important subject in 10th education, and you need to do well practice so that you can solve the higher classes math sums easily.
NCERT Solutions for Class 10 Maths Chapter 1 – Real Numbers
In this NCERT Solutions for Class 10 Maths Chapter 1, Real Numbers, you learn about a detailed knowledge about real numbers and irrational numbers. Here you read about Euclid’s Division Lemma that states “Given positive integers a and b. Get here NCERT Solutions for Class 10 Maths Chapter 1 in PDF Format.
Class 10 Maths Chapter 1 in English for CBSE Board
Class 10 Maths Exercise 1.1 in English
Class 10 Maths Exercise 1.2 in English
Class 10 Maths Chapter 1 in English for State Board
Class 10 Maths Exercise 1.1 in English
Class 10 Maths Exercise 1.2 in English
Class 10 Maths Exercise 1.3 in English
Class 10 Maths Exercise 1.4 in English
Tiwari Academy’s NCERT solutions are available in both English and Hindi. This makes them accessible to students from all language backgrounds.
Class 10 Maths Chapter 1 in Hindi Medium
Class 10 Maths Exercise 1.1 in Hindi
Class 10 Maths Exercise 1.2 in Hindi
Topics to be covered in Class 10 Maths Chapter 1 Real Numbers
Fundamental Theorem of Arithmetic – statements after reviewing work done earlier and after illustrating and motivating through examples, Proofs of irrationality of √2, √3 and √5.
NCERT Solutions for Class 10 Maths Chapter 2 – Polynomials
Student can get Class 10 Maths NCERT Solutions Chapter 2 – Polynomials with free of cost. Detailed solutions for all exercise sums by the experienced math teacher can be easily understood by the Class 10 Students.
Class 10 Maths Chapter 2 in English for CBSE Board
Class 10 Maths Exercise 2.1 in English
Class 10 Maths Exercise 2.2 in English
Class 10 Maths Chapter 2 in English for State Board
Class 10 Maths Exercise 2.1 in English
Class 10 Maths Exercise 2.2 in English
Class 10 Maths Exercise 2.3 in English
Class 10 Maths Exercise 2.4 in English
Tiwari Academy’s NCERT solutions are available for free online. Overall, Tiwari Academy is a great resource for students who want to excel in their Class 10 Maths exams and to prepare for success in their future.
Class 10 Maths Chapter 2 in Hindi Medium
Class 10 Maths Exercise 2.1 in Hindi
Class 10 Maths Exercise 2.2 in Hindi
Class 10 Maths Chapter 2 Polynomials Topics for Exams
Zeros of a polynomial. Relationship between zeros and coefficients of quadratic polynomials.
NCERT Solutions for Class 10 Maths Chapter 3 – Pair of Linear Equations in Two Variables
NCERT Solutions for class 10 math chapter 3 explains the concept of Pair of Linear Equations in Two Variables.
Class 10 Maths Chapter 3 in English for CBSE Board
Class 10 Maths Exercise 3.1 in English
Class 10 Maths Exercise 3.2 in English
Class 10 Maths Exercise 3.3 in English
Class 10 Maths Chapter 3 in English for CBSE Board
Class 10 Maths Exercise 3.1 in English
Class 10 Maths Exercise 3.2 in English
Class 10 Maths Exercise 3.3 in English
Class 10 Maths Exercise 3.4 in English
Class 10 Maths Exercise 3.5 in English
Class 10 Maths Exercise 3.6 in English
Class 10 Maths Exercise 3.7 in English
Class 10 Maths Chapter 3 in Hindi Medium
Class 10 Maths Exercise 3.1 in Hindi
Class 10 Maths Exercise 3.2 in Hindi
Class 10 Maths Exercise 3.3 in Hindi
Main Topics of Class 10 Maths Chapter 3 Pair of Linear Equations in two Variables
Pair of linear equations in two variables and graphical method of their solution, consistency/inconsistency. Algebraic conditions for number of solutions. Solution of a pair of linear equations in two variables algebraically – by substitution, by elimination. Simple situational problems.
NCERT Solutions for Class 10 Maths Chapter 4 – Quadratic Equations
NCERT Solutions for class 10 Maths chapter 4 will provide you to know the standard form of writing a quadratic equation.
Class 10 Maths Chapter 4 in English for CBSE Board
Class 10 Maths Exercise 4.1 in English
Class 10 Maths Exercise 4.2 in English
Class 10 Maths Exercise 4.3 in English
Class 10 Maths Chapter 4 in English for State Board
Class 10 Maths Exercise 4.1 in English
Class 10 Maths Exercise 4.2 in English
Class 10 Maths Exercise 4.3 in English
Class 10 Maths Exercise 4.4 in English
Class 10 Maths Chapter 4 in Hindi Medium
Class 10 Maths Exercise 4.1 in Hindi
Class 10 Maths Exercise 4.2 in Hindi
Class 10 Maths Exercise 4.3 in Hindi
Class 10 Maths Chapter 4 Quadratic Equations Rationalised Topics
Standard form of a quadratic equation ax² + bx + c = 0, (a ≠ 0). Solutions of quadratic equations (only real roots) by factorization, and by using quadratic formula. Relationship between discriminant and nature of roots. Situational problems based on quadratic equations related to day to day activities to be incorporated.
NCERT Solutions for Class 10 Maths Chapter 5 – Arithmetic Progressions
NCERT Solutions for class 10 Maths chapter 5 will introduce students to a new topic that is Arithmetic Progression which is also known as A.P.
Class 10 Maths Chapter 5 in English CBSE and State Board
Class 10 Maths Exercise 5.1 in English
Class 10 Maths Exercise 5.2 in English
Class 10 Maths Exercise 5.3 in English
Class 10 Maths Exercise 5.4 in English
Class 10 Maths Chapter 5 in Hindi Medium
Class 10 Maths Exercise 5.1 in Hindi
Class 10 Maths Exercise 5.2 in Hindi
Class 10 Maths Exercise 5.3 in Hindi
Class 10 Maths Exercise 5.4 in Hindi
Class 10 Maths Chapter 5 Arithmetic Progressions Topics for Board Exams
Motivation for studying Arithmetic Progression Derivation of the nth term and sum of the first n terms of A.P. and their application in solving daily life problems.
NCERT Solutions for Class 10 Maths Chapter 6 – Triangles
In this NCERT solution for class 10th Maths chapter 6, you learn about study those figures which have the same shapes but not necessarily the same size.
Class 10 Maths Chapter 6 in English for CBSE Board
Class 10 Maths Exercise 6.1 in English
Class 10 Maths Exercise 6.2 in English
Class 10 Maths Exercise 6.3 in English
Class 10 Maths Chapter 6 in English for State Board
Class 10 Maths Exercise 6.1 in English
Class 10 Maths Exercise 6.2 in English
Class 10 Maths Exercise 6.3 in English
Class 10 Maths Exercise 6.4 in English
Class 10 Maths Exercise 6.5 in English
Class 10 Maths Exercise 6.6 in English
Class 10 Maths Chapter 6 in Hindi Medium
Class 10 Maths Exercise 6.1 in Hindi
Class 10 Maths Exercise 6.2 in Hindi
Class 10 Maths Exercise 6.3 in Hindi
Class 10 Maths Chapter 6 Triangles Topics to be Covered
Definitions, examples, counter examples of similar triangles.
1. (Prove) If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
2. (Motivate) If a line divides two sides of a triangle in the same ratio, the line is parallel to the third side.
3. (Motivate) If in two triangles, the corresponding angles are equal, their corresponding sides are proportional and the triangles are similar.
4. (Motivate) If the corresponding sides of two triangles are proportional, their corresponding angles are equal and the two triangles are similar.
5. (Motivate) If one angle of a triangle is equal to one angle of another triangle and the sides including these angles are proportional, the two triangles are similar.
NCERT Solutions for Class 10 Maths Chapter 7– Coordinate Geometry
Here in this NCERT Solutions for class X Maths chapter 7 students will learn how to find the distance between two points if the coordinates are given.
Class 10 Maths Chapter 7 in English for CBSE Board
Class 10 Maths Exercise 7.1 in English
Class 10 Maths Exercise 7.2 in English
Class 10 Maths Chapter 7 in English for CBSE Board
Class 10 Maths Exercise 7.1 in English
Class 10 Maths Exercise 7.2 in English
Class 10 Maths Exercise 7.3 in English
Class 10 Maths Exercise 7.4 in English
To prepare for Class 10 Maths using Tiwari Academy or any similar online educational platform, you visit the Tiwari Academy website and navigate to the Class 10 Maths NCERT solutions section or the relevant resource area.
Class 10 Maths Chapter 7 in Hindi Medium
Class 10 Maths Exercise 7.1 in Hindi
Class 10 Maths Exercise 7.2 in Hindi
Class 10 Maths Solutions Chapter 7 Coordinate Geometry Main Points to Study
Concepts of coordinate geometry, graphs of linear equations. Distance formula. Section formula (internal division).
NCERT Solutions for Class 10 Maths Chapter 8 – Introduction to Trigonometry
You can get here NCERT Solutions for 10th Maths chapter 8 provided by the math expert teachers.
Class 10 Maths Chapter 8 in English for CBSE Board
Class 10 Maths Exercise 8.1 in English
Class 10 Maths Exercise 8.2 in English
Class 10 Maths Exercise 8.3 in English
Class 10 Maths Chapter 8 in English for State Board
Class 10 Maths Exercise 8.1 in English
Class 10 Maths Exercise 8.2 in English
Class 10 Maths Exercise 8.3 in English
Class 10 Maths Exercise 8.4 in English
Class 10 Maths Chapter 8 in Hindi Medium
Class 10 Maths Exercise 8.1 in Hindi
Class 10 Maths Exercise 8.2 in Hindi
Class 10 Maths Exercise 8.3 in Hindi
Class 10 Maths Chapter 8 Introduction to Trigonometry Topics for Session 2024-25
Trigonometric ratios of an acute angle of a right-angled triangle. Proof of their existence (well defined); motivate the ratios whichever are defined at 0o and 90o. Values of the trigonometric ratios of 30°, 45°, and 60°. Relationships between the ratios. Proof and applications of the identity sin²A + cos²A = 1. Only simple identities to be given.
NCERT Solutions for Class 10 Maths Chapter 9 – Some Applications of Trigonometry
Student can easily get FREE NCERT Solutions for class 10 Maths chapter 9 here. All sums are well explained and solved with an easy method so that 10th class student can clear all doubts. There is only one topic in this NCERT solutions for class 10 math chapter 9 Some Applications of Trigonometry.
Class 10 Maths Chapter 9 in English for CBSE and State Board
Class 10 Maths Exercise 9.1 in English
Class 10 Maths Chapter 9 in Hindi Medium
Class 10 Maths Exercise 9.1 in Hindi
Class 10 Maths Chapter 9 Applications of Trigonometry Focus Points
Angle of elevation, Angle of Depression. Simple problems on heights and distances. Problems should not involve more than two right triangles. Angles of elevation / depression should be only 30°, 45°, and 60°.
NCERT Solutions for Class 10 Maths Chapter 10 – Circles
Find the best NCERT Solutions for class 10 Maths chapter 10 here with free of cost. There are two topics in this chapter which covers: the tangent at any point of a circle, The lengths of tangents of the circle which are drawn from an external point etc.
Class 10 Maths Chapter 10 in English for CBSE and State Board
Class 10 Maths Exercise 10.1 in English
Class 10 Maths Exercise 10.2 in English
Class 10 Maths Textbook Solution Chapter 10 in Hindi Medium
Class 10 Maths Exercise 10.1 in Hindi
Class 10 Maths Exercise 10.2 in Hindi
The Main points of Class 10 Maths Chapter 10 Circles
Tangent to a circle at, point of contact.
1. (Prove) The tangent at any point of a circle is perpendicular to the radius through the point of contact.
2. (Prove) The lengths of tangents drawn from an external point to a circle are equal.
NCERT Solutions for Class 10 Maths Chapter 11 – Areas Related to Circles
You can download NCERT Solutions for class 10 Maths chapter 11 here. All solutions are well solved by professional math teachers. There are three topics covered in chapter 11 of grade X Maths NCERT.
Class 10 Maths Chapter 11 in English for CBSE Board
Class 10 Maths Exercise 11.1 in English
Class 10 Maths Chapter 11 in English for State Boards
Class 10 Maths Chapter 11 Exercise 11.1
Class 10 Maths Chapter 11 Exercise 11.2
Class 10 Maths Chapter 11 in Hindi Medium
Class 10 Maths Exercise 11.1 in Hindi
Course for Class 10 Maths Chapter 11 Areas Related to Circles
Area of sectors and segments of a circle. Problems based on areas and perimeter /circumference of the above said plane figures. (In calculating area of segment of a circle, problems should be restricted to central angle of 60°, 90° and 120° only.
NCERT Solutions for Class 10 Maths Chapter 12 – Surface Areas and Volumes
You can find there are a total of five exercises in this NCERT Solutions for class 10 mathematics chapter 12. Here you can learn about finding the surface area of cuboid, cone, sphere, cylinder and hemisphere etc. In this way student can get every info from the solutions of class 10 math chapter 12.
Class 10 Maths Chapter 12 in English for CBSE Board
Class 10 Maths Exercise 12.1 in English
Class 10 Maths Exercise 12.2 in English
Class 10 Maths Chapter 12 in English for State Boards
Class 10 Maths Chapter 12 Exercise 12.1
Class 10 Maths Chapter 12 Exercise 12.2
Class 10 Maths Chapter 12 Exercise 12.3
Class 10 Maths Chapter 12 in Hindi Medium
Class 10 Maths Exercise 12.1 in Hindi
Class 10 Maths Exercise 12.2 in Hindi
Class 10 Maths Chapter 12 Surface Areas and Volumes Syllabus
Surface areas and volumes of combinations of any two of the following: cubes, cuboids, spheres, hemispheres and right circular cylinders/cones.
NCERT Solutions for Class 10 Maths Chapter 13 – Statistics
Get here all exercises of NCERT Solutions for class 10 Maths chapter 13 with free of cost. The NCERT textbook for class 10 math chapter 13 Statistics covers cumulative frequency, cumulative frequency distribution, draw cumulative frequency curves, Cumulative frequency graph etc.
Class 10 Maths Chapter 13 in English for CBSE Board
Class 10 Maths Exercise 13.1 in English
Class 10 Maths Exercise 13.2 in English
Class 10 Maths Exercise 13.3 in English
Class 10 Maths Chapter 13 for State Boards
Class 10 Maths Chapter 13 Exercise 13.1
Class 10 Maths Chapter 13 Exercise 13.2
Class 10 Maths Chapter 13 Exercise 13.3
Class 10 Maths Chapter 13 Exercise 13.4
Class 10 Maths Chapter 13 Exercise 13.5
Class 10 Maths Chapter 13 in Hindi Medium
Class 10 Maths Exercise 13.1 in Hindi
Class 10 Maths Exercise 13.2 in Hindi
Class 10 Maths Exercise 13.3 in Hindi
Curriculum for Class 10 Maths Chapter 13 Statistics
Mean, median and mode of grouped data (bimodal situation to be avoided).
NCERT Solutions for Class 10 Maths Chapter 14 – Probability
In this last NCERT Solutions for class 10 math chapter 14, you learn about Probability, at the beginning of the chapter, you will learn the definition of probability. Get here all NCERT Solutions for Class 10 Maths Chapter 14 in PDF Format. Chapter 14 Probability covers the concept of probability with Simple problems.
Class 10 Maths Chapter 14 in English for CBSE Board
Class 10 Maths Exercise 14.1 in English
Class 10 Maths Chapter 14 in English for State Boards
Class 10 Maths Chapter 14 Exercise 14.1
Class 10 Maths Chapter 14 Exercise 14.2
Class 10 Maths Chapter 14 Exercise 14.3
Class 10 Maths Chapter 14 Exercise 14.4
Class 10 Maths Chapter 14 in Hindi Medium
Class 10 Maths Exercise 14.1 in Hindi
Class 10 Maths Chapter 14 Probability Focus Points
Classical definition of probability. Simple problems on finding the probability of an event.
Importance of Learning NCERT Solutions for Class 10 Maths from Tiwari Academy
NCERT Solutions for Class 10 Maths from Tiwari Academy are designed by the expert math teacher who has many years of experiences. It provides more benefits to the class 10 students by providing topic-wise and chapter-wise detailed knowledge with an easy method. There are also many other important to learn NCERT Solutions for Class 10 Maths from us. Let us discuss below:
Strengthens Your Basics
All chapter of class 10 Maths solutions are well designed by our experienced and professionals math experts. All topic-wise and chapter-wise answers are thoroughly researched and reviewed. Student can get more marks in their Board exam or in any competitive exam by using these solutions.
A Quick and Effective Revision Tool
NCERT solutions are created in such a manner that help students in the event of queries or doubts in a proper way. NCERT book is handy during exam preparation as it is the best quick and effective revision tool for your board exam.
Develops an Ability of Student to Solve Sums
All Maths solutions are well explained comprehensively, along with relevant and easy to understand examples. Student can have an idea of how to solve sums with step by step instructions.
Increases Student’s Confidence
All Maths solutions are provided with proper illustrations and examples. It helps build a conceptual understanding of all exercises by providing sufficient cases, and if the student gets practise well before the exam, then they can have high confidence.
How Class 10 Maths Solutions of NCERT Helpful for Board Exams?
Class 10 Maths Solutions of NCERT is very helpful for Board Exams as all the questions for Basic Mathematics were picked directly from NCERT textbooks. These solutions are well designed by the experienced Maths teacher. You can find many examples related the topics so that student can clear all concepts. It is a perfect guide to help you to score good marks in Board Exams. All solutions are based on the latest CBSE syllabus.
Preparation of Maths in Class 10
The solved examples help students to get a clear idea of the concepts. Our experts have created solutions that are easy to understand and follow as per the latest 2024-25 CBSE Syllabus and Marking scheme.
NCERT Solutions for Class 10 Maths for the first and second term you can get here free for CBSE session which are prescribed by the NCERT – National Council of Educational Research and Training (https://ncert.nic.in/). All these solutions are provided by our expert Maths teacher to help students in their board exam preparations.
How to study Class 10 Maths using NCERT Solutions?
Get here the revised and new NCERT Solutions for Class 10 Maths updated for 2024-25 exams. Creating a structured study plan for learning Class 10 Mathematics with the help of NCERT Solutions is essential for effective preparation. The consistency, practice, and understanding of fundamental concepts are crucial for success in Class 10 Maths. Stick to your study plan, and you’ll be well-prepared for your exams. Here’s a step-by-step study plan to help you excel in Class 10 Maths board exams.
- Step 1: Understand the Syllabus, Gather Resources like Books and Study Material.
- Step 2: Start with Basics, use NCERT Solutions and Take Notes of Important Terms.
- Step 3: Focus on Regular Practice, Self-Assessment and Seek Clarification.
- Step 4: Practice Time Management, Stay Healthy, make Revision and Review of course.
- Step 5: Maintain the practice time daily for Maths revision during Final Exam Preparation.
Step 1: Understand the Syllabus, Gather Resources like Books and Study Material.

Step 2: Start with Basics, use NCERT Solutions and Take Notes of Important Terms.
 Begin by reading the chapters in the 10th NCERT textbook thoroughly. Focus on understanding the fundamental concepts and principles. Ensure you have a balance between learning new concepts, practicing problems, and reviewing. After studying a chapter, solve the examples and exercises from the textbook. Use NCERT Solutions to check your answers, understand the correct solutions, and clarify doubts. While studying, take concise notes of important formulas, theorems, and key points. These notes helps for quick revision and preparation of chapters.
Begin by reading the chapters in the 10th NCERT textbook thoroughly. Focus on understanding the fundamental concepts and principles. Ensure you have a balance between learning new concepts, practicing problems, and reviewing. After studying a chapter, solve the examples and exercises from the textbook. Use NCERT Solutions to check your answers, understand the correct solutions, and clarify doubts. While studying, take concise notes of important formulas, theorems, and key points. These notes helps for quick revision and preparation of chapters.Step 3: Focus on Regular Practice, Self-Assessment and Seek Clarification.

Step 4: Practice Time Management, Stay Healthy, make Revision and Review of course.

Step 5: Maintain the practice time daily for Maths revision during Final Exam Preparation.

Which book is helpful for Class 10 Maths Basic and Standard?
There is no separate books for class 10 Math Standard and Basic. NCERT textbook for 10th Maths is the only book for both the courses and it is the best reference book which clear all the concept of all sums. This book is best to practice Mathematics for the CBSE Board Exam also. Keep in mind that the question paper of the board examination is based on NCERT textbook only, so do practice NCERT book thoroughly to score better in exams.
How to make CBSE Class 10 Maths Exam Easy?
The Central Board of Secondary Education (CBSE) is all set to provide the best combination of easy and difficult question to test all type of the students. Class 10th Maths paper is also good to score better but little bit difficult to score maximum. So, CBSE Class 10 Maths Exam is neither too easy nor to tough.
Which Textbook is enough for Class 10 Maths Boards Examination?
NCERT is the best study material among all reference books which help you get 90+ marks in board exam. If you have completed the NCERT textbook, must see the questions of NCERT Exemplar books also. Later on go through some practice papers and practice some sums of RD Sharma to enhance your marks, if required.
How to solve the toughest Chapters In Class 10 Maths?
Most of the chapters in NCERT Textbook 2024-25 are easy to solve for even an average student. Only few chapters are there which is considered as difficult one. The students found difficulty in some chapters in Class 10 Maths syllabus such as:
- Circle
- Triangles
- Trigonometry
- Application of trigonometry
- Surface area and volume
But doing practice well these above chapters then you can feel easier than before. Make sure you revised these difficult topics about 3-4 times before the exam.
Are the standard of CBSE 10th Maths Papers little bit higher than the usual school papers?
The question papers in CBSE Board exams are design in such a way, it is good for all type of students. The pattern of 10th Standard Board Examination is very simple to do and very easy to understand. But most of the people may misguide you a fear unnecessarily and do practice all the syllabus thoroughly, and you definitely score optimum marks in Class 10 Board Exam.